Translation simple (HU) : Différence entre versions
m (1 version) |
|||
| (15 révisions intermédiaires par 2 utilisateurs sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | ''<u>Traduction anglaise | + | ''<u>Traduction anglaise</u> : Lag (and rout) method'' |
| − | + | <u>Dernière mise à jour</u> : 16/06/2024 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | [[Modèle de propagation d’ondes de crue (HU)|Modèle de propagation]] en conduite ne prenant pas en compte l'[[Amortissement d'un hydrogramme (HU)|amortissement]] et l'étalement de [[Hydrogramme (HU)|l'hydrogramme]] lors de son transfert. | ||
| + | ==Formulation== | ||
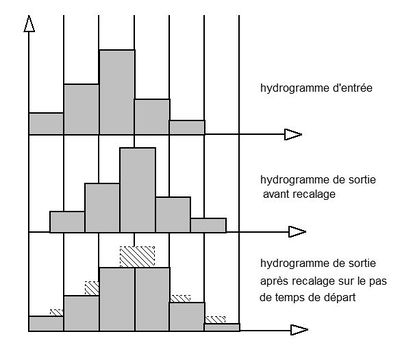
| − | < | + | L'hydrogramme à la sortie d'un tronçon a donc la même forme et la même durée qu'à l'entrée. Il est simplement décalé d'un temps <math>T_p</math>, qui est le temps moyen de propagation de l'onde dans le tronçon (''figure 1'') : |
| + | |||
| + | <center><math>Q_s(t) = Q_e(t-T_p)</math></center> | ||
Avec : | Avec : | ||
| + | * <math>Q_e(t)</math> : débit à l'amont du tronçon (m<sup>3</sup>/s) ; | ||
| + | * <math>Q_s(t)</math> : débit à l'aval (m<sup>3</sup>/s) ; | ||
| + | * <math>T_p</math> : temps moyen de propagation de l’onde (s). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[File:time offset 1.JPG|500px|center|thumb|<center>''<u>Figure 1</u> : Représentation graphique des hydrogrammes d'entrée et de sortie.''</center>]] | ||
| + | ==Mode de discrétisation et diffusion numérique== | ||
| − | + | Le temps <math>T_p</math> est égal au rapport de la longueur du tronçon à la [[Célérité (HU)|célérité]] de l'onde. La célérité de l'onde est pour sa part le plus souvent évaluée (en l'absence de mesures) en calculant une vitesse moyenne de l'eau. L'une des méthodes les plus simples consiste à assimiler la vitesse de l'onde à la vitesse de l'eau en régime uniforme, correspondant à 80% du débit maximum de l'hydrogramme d'entrée. Cette méthode donne de bons résultats en l'absence d'influences aval marquées. Il est important de noter que si l'on travaille sur des hydrogrammes discrétisés dans le temps (fonctions en escalier), la recomposition de l'hydrogramme de sortie sur une base de temps fixe de pas <math>Δt</math>, ne permet pas d'appliquer strictement la méthode. Deux techniques peuvent alors être utilisées : | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | * Soit on choisit un pas de discrétisation <math>Δt</math> petit par rapport à <math>T_p</math> et on arrondit <math>T_p</math> à un nombre entier de pas de temps : | ||
| − | <center> | + | <center><math>T_p = n*\Delta t</math></center> |
| + | * Soit on conserve la valeur exacte de <math>T_p</math> et on recompose l'hydrogramme sur la base de temps fixe. On introduit alors un amortissement numérique de l'hydrogramme de sortie (''figure 2''). | ||
| − | |||
| − | |||
| − | + | [[File:time offset 2.JPG|400px|center|thumb|<center>''Figure 2 : Amortissement artificiel dû à la discrétisation.''</center>]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Ce modèle peut être considéré comme un cas particulier de la méthode de Muskingum (paramètre <math>α = 0.5</math>) et son intérêt est limité aux situations dans lesquelles on s'intéresse seulement à l’obtention d’une solution approximative rapide. | |
| − | désigne souvent ces méthodes sous le nom de méthodes de time offset | + | |
| − | alors que la traduction anglaise est lag methods. | + | <u>Attention</u> : Curieusement, en français, on désigne souvent ces méthodes sous le nom de méthodes de time offset alors que la traduction anglaise est ''lag methods''. |
| − | [[Catégorie: | + | [[Catégorie:Dictionnaire_DEHUA]] |
| + | [[Catégorie:Modélisation_des_écoulements_en_réseau_et_en_rivière_(HU)]] | ||
Version actuelle en date du 14 juin 2024 à 14:57
Traduction anglaise : Lag (and rout) method
Dernière mise à jour : 16/06/2024
Modèle de propagation en conduite ne prenant pas en compte l'amortissement et l'étalement de l'hydrogramme lors de son transfert.
[modifier] Formulation
L'hydrogramme à la sortie d'un tronçon a donc la même forme et la même durée qu'à l'entrée. Il est simplement décalé d'un temps $ T_p $, qui est le temps moyen de propagation de l'onde dans le tronçon (figure 1) :
Avec :
- $ Q_e(t) $ : débit à l'amont du tronçon (m3/s) ;
- $ Q_s(t) $ : débit à l'aval (m3/s) ;
- $ T_p $ : temps moyen de propagation de l’onde (s).
[modifier] Mode de discrétisation et diffusion numérique
Le temps $ T_p $ est égal au rapport de la longueur du tronçon à la célérité de l'onde. La célérité de l'onde est pour sa part le plus souvent évaluée (en l'absence de mesures) en calculant une vitesse moyenne de l'eau. L'une des méthodes les plus simples consiste à assimiler la vitesse de l'onde à la vitesse de l'eau en régime uniforme, correspondant à 80% du débit maximum de l'hydrogramme d'entrée. Cette méthode donne de bons résultats en l'absence d'influences aval marquées. Il est important de noter que si l'on travaille sur des hydrogrammes discrétisés dans le temps (fonctions en escalier), la recomposition de l'hydrogramme de sortie sur une base de temps fixe de pas $ Δt $, ne permet pas d'appliquer strictement la méthode. Deux techniques peuvent alors être utilisées :
- Soit on choisit un pas de discrétisation $ Δt $ petit par rapport à $ T_p $ et on arrondit $ T_p $ à un nombre entier de pas de temps :
- Soit on conserve la valeur exacte de $ T_p $ et on recompose l'hydrogramme sur la base de temps fixe. On introduit alors un amortissement numérique de l'hydrogramme de sortie (figure 2).
Ce modèle peut être considéré comme un cas particulier de la méthode de Muskingum (paramètre $ α = 0.5 $) et son intérêt est limité aux situations dans lesquelles on s'intéresse seulement à l’obtention d’une solution approximative rapide.
Attention : Curieusement, en français, on désigne souvent ces méthodes sous le nom de méthodes de time offset alors que la traduction anglaise est lag methods.
 S'abonner à un flux RSS
S'abonner à un flux RSS