Modèle de propagation d’ondes de crue (HU)

Traduction anglaise : Flow routing model, Flood routing model

Dernière mise à jour : 16/05/2024

Classe de modèles conceptuels (parfois empiriques) permettant de simuler la propagation d'une onde de crue dans un système hydrologique en représentant son décalage temporel et son amortissement ; on parle également de modèle de transfert d'onde de crue, et parfois de modèle de transport (il vaut cependant mieux éviter ce dernier terme qui peut porter à confusion avec les modèles de transport solide).

Formulation mathématique

Les modèles conceptuels de propagation reposent principalement sur l'équation de continuité :

$ Q_s(t) = Q_e(t)- \frac{dV_s(t)}{dt} $

Avec :

• $ Q_e(t) $ : débit à l'entrée du tronçon (m³/s) ;
• $ Q_s(t) $ : débit à la sortie du tronçon (m³/s) ;
• $ V_s(t) $ : volume stocké dans le tronçon (m³).

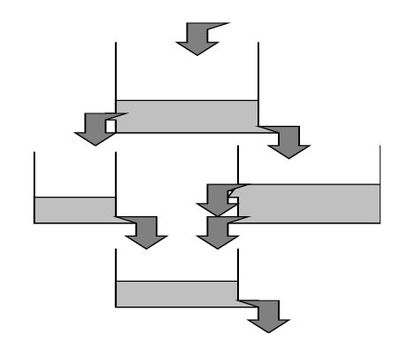
La deuxième équation est généralement une équation de stockage reliant le volume stocké aux débits à l'amont et/ou à l'aval du tronçon. Ces modèles peuvent souvent être représentés par des réservoirs (figure 1). Leur formulation est donc proche, voire parfois strictement identique, à celle de certaines des fonctions de transfert des modèles hydrologiques (ce qui conduit parfois à les qualifier, improprement, de modèle hydrologique).

Il est possible d'établir un lien entre certains modèles de propagation d'onde de crue et des modèles simplifiés issus des équations de Barré de Saint venant (Cunge, 1969 ; Thibault et al., 1980).

Figure 1 : Exemple de modèle à réservoirs.

Les modèles de transfert d'onde les plus connus sont le modèle Muskingum, le modèle de translation simple et le modèle de stock.

Avantages et inconvénients des modèles de transfert d'onde

Le seul but de cette famille de modèles est de reproduire le décalage temporel et la déformation de l'hydrogramme entre l'amont et l'aval d'un tronçon, et plus généralement dans un système hydrologique. Pour accéder à des grandeurs physiques différentes du débit (hauteur ou vitesse en particulier, ce qui peut être nécessaire, par exemple pour évaluer le risque d'inondation), il est nécessaire d'utiliser un post-processeur permettant le calcul de la ligne d'eau connaissant le débit. Cette approche est cependant assez peu pertinente car la relation entre hauteur et débit n'est pas univoque.

Leurs principaux avantages sont leur stabilité, le fait de ne nécessiter que peu d'informations sur le système hydrologique modélisé et la rapidité des calculs. Ils négligent cependant de nombreux phénomènes souvent importants dans la propagation des crues, en particulier influence aval, mise en charge ou débordement (dans le cas des réseaux d'assainissement) et inondation du lit majeur dans le cas des cours d'eau.

La puissance des moyens de calcul aujourd'hui disponibles ont réduit leur intérêt et la plupart des modèles hydrauliques utilisent les équations complètes de Barré de saint Venant pour représenter la propagation des crues. Voir Modèles d'écoulement en réseau et en rivière (HU).

Attention : Le mot anglais flood routing model désigne tous les modèles de propagation en conduite, y compris ceux fondés sur les équations de Barré de Saint Venant.

Bibliographie :

• Cunge, J.A. (1969) : Au sujet d'une méthode de propagation de crue ; Journal of Hydraulics Research ; n°7 ; 1969 ; pp 205-230.
• Thibault, S., Chocat, B., Botta, H. (1980) : Relations théoriques entre différents modèles d'écoulement et de ruissellement utilisés en hydrologie urbaine ; Journal of Hydrology ; Volume 48, Issues 3–4, November 1980, Pages 313-326.

Pour en savoir plus :

• B.26 - Modélisation hydraulique