Stock (modèle de) (HU)

Traduction anglaise : Storage model

Dernière mise à jour : 16/05/2024

Modèle de propagation non linéaire permettant la simulation simplifiée du fonctionnement hydraulique des systèmes d'assainissement. Leur seul but est de reproduire la déformation de l'hydrogramme entre l'amont et l'aval d'un tronçon (Chocat, 1977), (Mottie et al., 1997). Comme tous les modèles de transfert d'onde, les modèles de stock reposent sur l'équation de continuité qui s'écrit à tout instant $ t $ sous la forme (relation (1) :

$ Q_s(t) = Q_e(t)- \frac{dV_s(t)}{dt}\qquad (1) $

Avec :

• $ Q_e(t) $ :  débit à l'entrée du tronçon au temps t (m³/s) ;
• $ Q_s(t) $ :  débit à la sortie du tronçon au temps t (m³/s) ;
• $ V_s(t) $ :  volume stocké dans le tronçon au temps t (m³).

Figure 1 : Exemple de lignes d'eau prises en compte dans le modèle de stock pour évaluer le volume stocka en fonction du type d'écoulement : (1) écoulement à surface libre non influencé par l'aval, (2) : écoulement en charge, (3) écoulement partiellement en charge, (4) : écoulement partiellement influencé par l'aval.

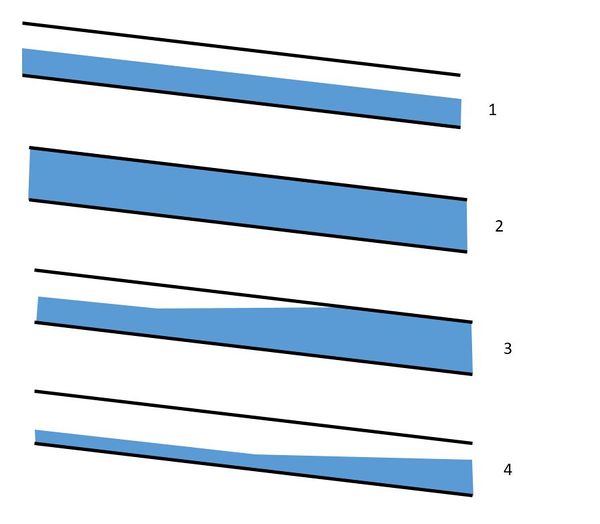
La deuxième équation relie le volume stocké aux conditions instantanées régnant dans l'écoulement, elles mêmes évaluées en faisant des hypothèses géométriques simples (par exemple ligne d'eau parallèle au fond en régime torrentiel ou ligne d'eau horizontale dans le cas d'une influence aval (figure 1 et relation (2)).

$ V_s(t) = L.(α(t). S_e(t) + (1-α(t)). S_s(t))\qquad (2) $

Avec :

• $ S_e(t) $ : Section mouillée à l'amont du tronçon (m²/s) ($ S_e(t) $ est une fonction de $ Q_e(t) $ et des conditions d'écoulement) ;
• $ Q_s(t) $ : débit à la sortie du tronçon (m³/s) ($ S_s(t) $ est une fonction de $ Q_s(t) $ et des conditions d'écoulement) ;
• $ L(t) $ : longueur du tronçon (m).
• $ α(t) $ : paramètre sans dimension compris entre 0 et 1 et fonction de la forme de la ligne d'eau.

Les modèles de stock nécessitent un calcul itératif à chaque pas de temps (le calcul des débits nécessite la connaissance de $ S_e(t) $ et de $ S_s(t) $, donc de la ligne d'eau et le calcul de la ligne d'eau nécessite la connaissance des débits). Ce calcul itératif est généralement conduit par des méthodes de prédiction-correction.

L'avantage principal des modèles de stock est leur vitesse de calcul et leur stabilité. Leur inconvénient principal réside dans le fait qu'ils négligent les effets dynamiques. Ils peuvent également être difficiles à utiliser dans le cas des réseaux maillés. Ces modèles ont perdu de leur intérêt avec le développement de logiciels performants utilisant les équations complètes de Barré de Saint Venant.

Bibliographie :

• Chocat, B. (1977) : Un modèle de simulation des écoulements dans les réseaux d'assainissement pluvial ; thèse Docteur ingénieur ; INSA Lyon ; 304p.
• Mottie, H., Chocat, B., Blanpain, O. (1997) : A storage model for the simulation of the hydraulic behaviour of drainage network; Water Science and Technology ; Volume 36 ; Issues 8–9 ; Pp 57-63.