Horton (modèle de) (HU) : Différence entre versions
(→Choix de fc) |
|||
| (11 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Horton's model'' | ''<u>Traduction anglaise</u> : Horton's model'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 22/05/2024 |
| − | Modèle empirique de représentation de [[Infiltration (HU)|l'infiltration]] sur les sols perméables. | + | Modèle empirique de représentation de [[Infiltration (HU)|l'infiltration]] sur les sols perméables utilisable comme [[Fonction de production et fonction de transfert (HU)|fonction de production]] dans les [[Modèle hydrologique (HU)|modèles hydrologiques]]. |
==Formulation et utilisation pratique== | ==Formulation et utilisation pratique== | ||
| − | La modèle de Horton consiste à exprimer la capacité d'infiltration d'un sol au temps <math>t</math> sous la forme suivante : | + | La modèle de Horton consiste à exprimer la [[Capacité d’infiltration (HU)|capacité d'infiltration]] d'un sol au temps <math>t</math> sous la forme suivante : |
| − | + | ||
<center><math>f(t) = f_c+(f_0-f_c).e^{-k.t}</math></center> | <center><math>f(t) = f_c+(f_0-f_c).e^{-k.t}</math></center> | ||
| − | |||
Avec : | Avec : | ||
| − | * <math>f_o</math> : capacité d'infiltration maximum du sol ; | + | * <math>f_o</math> : capacité d'infiltration maximum du sol (correspondant à un sol sec) (mm/h) ; |
| − | * <math>f_c</math> : capacité d'infiltration du sol saturé ; | + | * <math>f_c</math> : capacité d'infiltration du sol saturé (normalement égale à la [[Conductivité hydraulique (HU)|conductivité hydraulique]] du sol) (mm/h); |
| − | * <math>k</math> : constante de temps positive. | + | * <math>k</math> : constante de temps positive (h<sup>-1</sup> si les temps sont en heures). |
| − | + | Il est important de noter que la saturation du sol ne peut suivre la loi de saturation théorique que si l'intensité de pluie reste en permanence supérieure à la capacité d'infiltration du sol. Dans le cas contraire le sol absorbe toute l'eau précipitée, le taux d'infiltration réel est donc égal à l'intensité de la pluie et le sol se sature moins vite. En général, la courbe d'infiltration théorique est supérieure à l'intensité au début de la pluie, puis elle devient inférieure à cette dernière. La méthode la plus simple pour tenir compte de ce phénomène consiste à décaler la courbe d'infiltration dans le temps, de manière à ce que le ruissellement ne commence que lorsque la hauteur d'eau infiltrée devient égale à la hauteur d'eau précipitée. | |
| − | |||
| + | [[File:Horton1.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Principe du décalage de la courbe d'infiltration.''</center>]] | ||
| − | + | La ''figure 1'' schématise ce principe. Le décalage temporel de la courbe théorique d'infiltration est tel que les volumes grisés situés au-dessus et en dessous de l'hydrogramme soient égaux. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Les temps <math>t_0</math> et <math>t_1</math> sont tels que : | Les temps <math>t_0</math> et <math>t_1</math> sont tels que : | ||
| − | |||
<center><math>\int_0^{t_0}i(t).dt=\int_0^{t_1-t_0}f(t).dt</math></center> | <center><math>\int_0^{t_0}i(t).dt=\int_0^{t_1-t_0}f(t).dt</math></center> | ||
| − | |||
et | et | ||
| − | |||
<center><math>i(t_1)=f(t_1-t_0)</math></center> | <center><math>i(t_1)=f(t_1-t_0)</math></center> | ||
| − | |||
== Choix des paramètres == | == Choix des paramètres == | ||
| − | La principale difficulté consiste à évaluer correctement les paramètres <math>f_0</math>, <math>f_c</math> et <math>k</math>. Ceux-ci varient beaucoup avec les caractéristiques physiques du sol (porosité), mais aussi avec sa teneur initiale en | + | La principale difficulté consiste à évaluer correctement les paramètres <math>f_0</math>, <math>f_c</math> et <math>k</math>. Ceux-ci varient beaucoup avec les caractéristiques physiques du sol ([[Porosité (HU)|porosité]], [[Conductivité hydraulique (HU)|conductivité hydraulique]], mais aussi avec sa [[Teneur en eau (HU)|teneur initiale en eau]], sa couverture végétale, la dimension des gouttes de pluie, la température, la pente, etc. Ils peuvent être mesurés en laboratoire, in situ (par des essais de perméabilité ou sous pluie artificielle), calés à partir de mesures pluie-débit ou estimés à partir de valeurs fournies par la littérature. |
===Choix de ''f<sub>c</sub>''=== | ===Choix de ''f<sub>c</sub>''=== | ||
| − | Les valeurs de <math>f_c</math> peuvent par exemple être choisies en utilisant le tableau | + | Les valeurs de <math>f_c</math> peuvent par exemple être choisies en utilisant le tableau de la ''figure 2'' (en mm/h): |
| − | + | ||
| − | [[File: | + | [[File:Horton_figure1.JPG|800px|center|thumb|<center>''<u>Figure 2</u> : Plages de variation du paramètre <math>f_c</math> en fonction de la nature du sol et du type de couverture végétale.''</center>]] |
===Choix de ''f<sub>0</sub>''=== | ===Choix de ''f<sub>0</sub>''=== | ||
| Ligne 63 : | Ligne 53 : | ||
* Si le sol est saturé en humidité au début de l'écoulement on peut considérer que <math>f_0</math> est égal à <math>f_c</math> ; | * Si le sol est saturé en humidité au début de l'écoulement on peut considérer que <math>f_0</math> est égal à <math>f_c</math> ; | ||
* Si le sol est sec, on utilise généralement le modèle de Holtan : | * Si le sol est sec, on utilise généralement le modèle de Holtan : | ||
| + | |||
<center><math>f_0 = 4.f_c</math></center> | <center><math>f_0 = 4.f_c</math></center> | ||
| Ligne 69 : | Ligne 60 : | ||
===Choix de ''k''=== | ===Choix de ''k''=== | ||
| − | Le paramètre <math>k</math> décrit la vitesse avec laquelle le sol se sature. Sa valeur dépend principalement de l'épaisseur de terre végétale. Si on exprime le temps en | + | Le paramètre <math>k</math> décrit la vitesse avec laquelle le sol se sature. Sa valeur dépend principalement de l'épaisseur de terre végétale. Si on exprime le temps en heures, la valeur de <math>k</math> est généralement comprise entre <math>0{,}3</math> et <math>3</math>h<sup>-1</sup>, ce qui correspond à des temps de saturation du sol de quelques heures (voir tableau de la ''figure 3''). |
| + | |||
| + | |||
| + | [[File:horton_tableau.JPG|600px|center|thumb|<center>''<u>Figure 3</u> : Valeur de k en fonction du temps de saturation du sol.''</center>]] | ||
== Intérêt et limites == | == Intérêt et limites == | ||
| − | Ce modèle donne une bonne approximation des courbes d'infiltration dans un sol humide dans son horizon superficiel, ou dans un sol fortement végétalisé. Elle convient en revanche très mal pour les sols nus et secs où les problèmes d'interface eau/air dans la zone superficielle sont importants. | + | Ce modèle donne une bonne approximation des courbes d'infiltration dans un sol humide dans son horizon superficiel, ou dans un sol fortement végétalisé. Elle convient en revanche très mal pour les sols nus et secs où les problèmes d'interface eau/air dans la zone superficielle sont importants. Le principal problème d'utilisation de ce modèle réside dans le choix des paramètres. |
<u>Bibliographie</u> : | <u>Bibliographie</u> : | ||
Version actuelle en date du 22 mai 2024 à 14:24
Traduction anglaise : Horton's model
Dernière mise à jour : 22/05/2024
Modèle empirique de représentation de l'infiltration sur les sols perméables utilisable comme fonction de production dans les modèles hydrologiques.
Sommaire |
[modifier] Formulation et utilisation pratique
La modèle de Horton consiste à exprimer la capacité d'infiltration d'un sol au temps $ t $ sous la forme suivante :
Avec :
- $ f_o $ : capacité d'infiltration maximum du sol (correspondant à un sol sec) (mm/h) ;
- $ f_c $ : capacité d'infiltration du sol saturé (normalement égale à la conductivité hydraulique du sol) (mm/h);
- $ k $ : constante de temps positive (h-1 si les temps sont en heures).
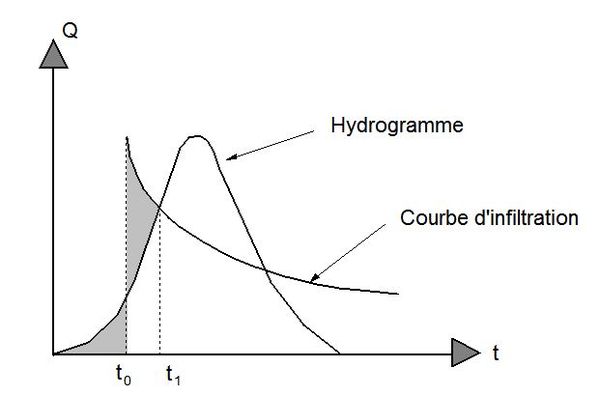
Il est important de noter que la saturation du sol ne peut suivre la loi de saturation théorique que si l'intensité de pluie reste en permanence supérieure à la capacité d'infiltration du sol. Dans le cas contraire le sol absorbe toute l'eau précipitée, le taux d'infiltration réel est donc égal à l'intensité de la pluie et le sol se sature moins vite. En général, la courbe d'infiltration théorique est supérieure à l'intensité au début de la pluie, puis elle devient inférieure à cette dernière. La méthode la plus simple pour tenir compte de ce phénomène consiste à décaler la courbe d'infiltration dans le temps, de manière à ce que le ruissellement ne commence que lorsque la hauteur d'eau infiltrée devient égale à la hauteur d'eau précipitée.
La figure 1 schématise ce principe. Le décalage temporel de la courbe théorique d'infiltration est tel que les volumes grisés situés au-dessus et en dessous de l'hydrogramme soient égaux.
Les temps $ t_0 $ et $ t_1 $ sont tels que :
et
[modifier] Choix des paramètres
La principale difficulté consiste à évaluer correctement les paramètres $ f_0 $, $ f_c $ et $ k $. Ceux-ci varient beaucoup avec les caractéristiques physiques du sol (porosité, conductivité hydraulique, mais aussi avec sa teneur initiale en eau, sa couverture végétale, la dimension des gouttes de pluie, la température, la pente, etc. Ils peuvent être mesurés en laboratoire, in situ (par des essais de perméabilité ou sous pluie artificielle), calés à partir de mesures pluie-débit ou estimés à partir de valeurs fournies par la littérature.
[modifier] Choix de fc
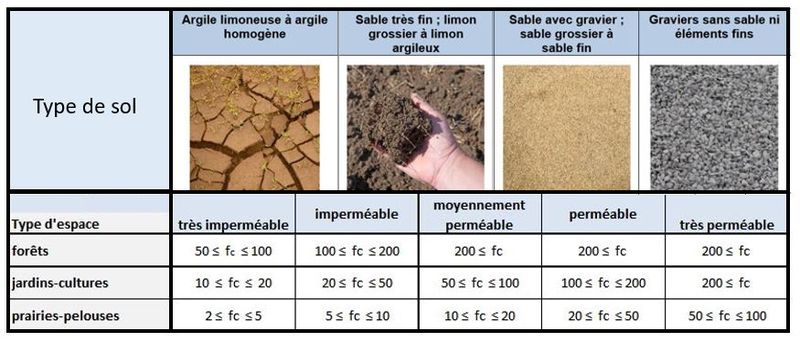
Les valeurs de $ f_c $ peuvent par exemple être choisies en utilisant le tableau de la figure 2 (en mm/h):
[modifier] Choix de f0
La valeur de $ f_0 $ peut pour sa part être choisie en fonction de $ f_c $ en tenant compte en particulier de la pluviosité antécédente.
- Si le sol est saturé en humidité au début de l'écoulement on peut considérer que $ f_0 $ est égal à $ f_c $ ;
- Si le sol est sec, on utilise généralement le modèle de Holtan :
[modifier] Choix de k
Le paramètre $ k $ décrit la vitesse avec laquelle le sol se sature. Sa valeur dépend principalement de l'épaisseur de terre végétale. Si on exprime le temps en heures, la valeur de $ k $ est généralement comprise entre $ 0{,}3 $ et $ 3 $h-1, ce qui correspond à des temps de saturation du sol de quelques heures (voir tableau de la figure 3).
[modifier] Intérêt et limites
Ce modèle donne une bonne approximation des courbes d'infiltration dans un sol humide dans son horizon superficiel, ou dans un sol fortement végétalisé. Elle convient en revanche très mal pour les sols nus et secs où les problèmes d'interface eau/air dans la zone superficielle sont importants. Le principal problème d'utilisation de ce modèle réside dans le choix des paramètres.
Bibliographie :
- Horton, R.E. (1931) : The field, scope, and status of the science of hydrology ; Eos, Transactions American Geophysical Union, 1931 - Wiley Online Library
 S'abonner à un flux RSS
S'abonner à un flux RSS