Géostatistique (HU) : Différence entre versions
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Geostatistic'' | ''<u>Traduction anglaise</u> : Geostatistic'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 09/09/2021 |
Application de la théorie des probabilités et de celle des distributions à l'étude de phénomènes aléatoires se développant dans l'espace en vue de leur estimation. | Application de la théorie des probabilités et de celle des distributions à l'étude de phénomènes aléatoires se développant dans l'espace en vue de leur estimation. | ||
| Ligne 7 : | Ligne 7 : | ||
==Origine et principes de la géostatistique== | ==Origine et principes de la géostatistique== | ||
| − | Le terme géostatistique a été créé dans les années 1960 par Matheron (1962) dans le cadre de la recherche minière et pétrolière. Des méthodes tout à fait comparables ont été développées | + | Le terme géostatistique a été créé dans les années 1960 par Matheron (1962) dans le cadre de la recherche minière et pétrolière. Des méthodes tout à fait comparables ont été développées à la même époque dans le domaine de la météorologie sous le nom d'analyse objective par Gandin (1963). Dans les deux cas, l'objectif était d'étudier un phénomène dit régionalisé, connu en certains points, et que l'on voulait représenter par une fonction continue. |
| − | La géostatistique dite transitive se contente d'un niveau d'abstraction purement descriptif. Dans ce cas on se contente de construire une fonction continue représentant au mieux les valeurs de la variable là où elles sont connues. Ce traitement se fait en utilisant des techniques d'interpolation spatiale (voir [[Krigeage (HU)|krigeage]] ou fonctions [[Spline (fonction) (HU)|splines]]). | + | La géostatistique dite transitive se contente d'un niveau d'abstraction purement descriptif. Dans ce cas on se contente de construire une fonction continue représentant au mieux les valeurs de la variable là où elles sont connues. Ce traitement se fait en utilisant des techniques d'interpolation spatiale (voir [[Krigeage (HU)|krigeage]] ou fonctions [[Spline (fonction) (HU)|splines]]) ou d'approximation (méthode des moindres carrés par exemple). |
| − | On peut également considérer la variable régionalisée comme la réalisation d’une fonction aléatoire. On parle alors de géostatistique intrinsèque. Ce choix permet d’utiliser des outils probabilistes puissants, en compliquant cependant la formulation et sans pouvoir tenir compte des éléments de connaissance physique existant éventuellement sur le phénomène. | + | On peut également considérer la variable régionalisée comme la réalisation d’une fonction aléatoire. On parle alors de géostatistique intrinsèque. Ce choix permet d’utiliser des outils probabilistes puissants, en compliquant cependant la formulation et sans pouvoir tenir compte des éléments de connaissance physique existant éventuellement sur le phénomène (par exemple rôle du relief sur la pluie). |
==Utilisation en hydrologie== | ==Utilisation en hydrologie== | ||
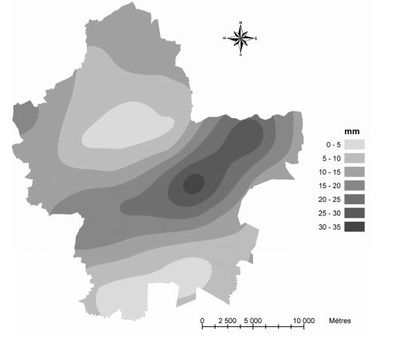
| − | La principale utilisation de ces méthodes en hydrologie est la représentation spatiale | + | La principale utilisation de ces méthodes en hydrologie est la représentation spatiale de précipitations mesurée uniquement sur un ensemble discret de points correspondant au réseau de [[Pluviomètre (HU)|pluviomètres]]. L'estimation recherchée peut être ponctuelle (intensité instantanée ou hauteur d'eau en tout point du bassin versant) ou bien elle peut être surfacique ([[Lame d'eau (HU)|lame d'eau]] moyenne sur un bassin versant). Voir par exemple Creutin (1979) ou Renard et Comby (2006), (2007). |
Pour satisfaire des critères statistiques (non-biais et erreur quadratique moyenne minimale des estimations) ces méthodes recourent à des hypothèses sur la structure statistique du phénomène : essentiellement la stationnarité des moments d'ordre 1 (la moyenne du phénomène ne dépend pas du point d'observation) et 2 (la covariance du phénomène ne dépend que de la distance séparant les points que l'on considère et non de l'endroit où sont situés ces points). Dans le cas des champs de pluie, et singulièrement aux échelles de temps et d'espace où l'intermittence est importante (cas des applications à l'hydrologie urbaine par exemple) ces hypothèses sont irréalistes et ces méthodes (par exemple les méthodes de [[Krigeage (HU)|krigeage]]) doivent être adaptées et utilisées avec discernement. | Pour satisfaire des critères statistiques (non-biais et erreur quadratique moyenne minimale des estimations) ces méthodes recourent à des hypothèses sur la structure statistique du phénomène : essentiellement la stationnarité des moments d'ordre 1 (la moyenne du phénomène ne dépend pas du point d'observation) et 2 (la covariance du phénomène ne dépend que de la distance séparant les points que l'on considère et non de l'endroit où sont situés ces points). Dans le cas des champs de pluie, et singulièrement aux échelles de temps et d'espace où l'intermittence est importante (cas des applications à l'hydrologie urbaine par exemple) ces hypothèses sont irréalistes et ces méthodes (par exemple les méthodes de [[Krigeage (HU)|krigeage]]) doivent être adaptées et utilisées avec discernement. | ||
Version du 9 septembre 2021 à 09:13
Traduction anglaise : Geostatistic
Dernière mise à jour : 09/09/2021
Application de la théorie des probabilités et de celle des distributions à l'étude de phénomènes aléatoires se développant dans l'espace en vue de leur estimation.
Origine et principes de la géostatistique
Le terme géostatistique a été créé dans les années 1960 par Matheron (1962) dans le cadre de la recherche minière et pétrolière. Des méthodes tout à fait comparables ont été développées à la même époque dans le domaine de la météorologie sous le nom d'analyse objective par Gandin (1963). Dans les deux cas, l'objectif était d'étudier un phénomène dit régionalisé, connu en certains points, et que l'on voulait représenter par une fonction continue.
La géostatistique dite transitive se contente d'un niveau d'abstraction purement descriptif. Dans ce cas on se contente de construire une fonction continue représentant au mieux les valeurs de la variable là où elles sont connues. Ce traitement se fait en utilisant des techniques d'interpolation spatiale (voir krigeage ou fonctions splines) ou d'approximation (méthode des moindres carrés par exemple).
On peut également considérer la variable régionalisée comme la réalisation d’une fonction aléatoire. On parle alors de géostatistique intrinsèque. Ce choix permet d’utiliser des outils probabilistes puissants, en compliquant cependant la formulation et sans pouvoir tenir compte des éléments de connaissance physique existant éventuellement sur le phénomène (par exemple rôle du relief sur la pluie).
Utilisation en hydrologie
La principale utilisation de ces méthodes en hydrologie est la représentation spatiale de précipitations mesurée uniquement sur un ensemble discret de points correspondant au réseau de pluviomètres. L'estimation recherchée peut être ponctuelle (intensité instantanée ou hauteur d'eau en tout point du bassin versant) ou bien elle peut être surfacique (lame d'eau moyenne sur un bassin versant). Voir par exemple Creutin (1979) ou Renard et Comby (2006), (2007).
Pour satisfaire des critères statistiques (non-biais et erreur quadratique moyenne minimale des estimations) ces méthodes recourent à des hypothèses sur la structure statistique du phénomène : essentiellement la stationnarité des moments d'ordre 1 (la moyenne du phénomène ne dépend pas du point d'observation) et 2 (la covariance du phénomène ne dépend que de la distance séparant les points que l'on considère et non de l'endroit où sont situés ces points). Dans le cas des champs de pluie, et singulièrement aux échelles de temps et d'espace où l'intermittence est importante (cas des applications à l'hydrologie urbaine par exemple) ces hypothèses sont irréalistes et ces méthodes (par exemple les méthodes de krigeage) doivent être adaptées et utilisées avec discernement.
Bibliographie :
- Creutin, J.-D. (1979) : Méthode d'interpolation de champs hydrométéorologiques. Comparaison et application à une série d'épisodes pluvieux Cévenols ; Thèse DI ; IMG-INPG ; Grenoble ; 1979.
- Gandin, L. S. : 1965, Objective analysis of meteorological fields: U.S. Dept. Commerce and National Science Foundation 1Washington, D.C.), 242 p. (Original in Russian, ob ektivnyi analiz meteorologicheskikh polei, 1963).
- Matheron, G. (1962) : Traité de Géostatistique appliquée. Tome 1, Éditions Technip, Paris, 1962, 334 p
- Renard, F. & Comby, J. (2006): Évaluation de techniques d’interpolation spatiale de la pluie en milieu urbain pour une meilleure gestion d’événements extrêmes : le cas du Grand Lyon ; La Houille blanche N°6, 2006 ; pp 73-78 ;
- Renard, F & Comby, J. (2007): Caractérisation de l’aléa pluviométrique en milieu urbain à partir d’interpolations spatiales : le cas du Grand Lyon ; Climatologie, 2007, p. 131-144. téléchargeable sur : http://lodel.irevues.inist.fr/climatologie/index.php?id=782
Pour en savoir plus : Statistiques spatiales : introduction à la géostatistique
 S'abonner à un flux RSS
S'abonner à un flux RSS