Validation d'un modèle (HU) : Différence entre versions

Version du 22 juillet 2021 à 17:48

Traduction anglaise : Model validation, Model verification

Dernière mise à jour : 22/07/2021

En toute rigueur, processus par lequel on démontre la validité d’un modèle en s'appuyant sur des preuves évidentes, sur le raisonnement ou sur des données totalement indépendantes (obtenues sur d'autres sites ou représentatives d’un autre aspect) de celles ayant permis de le construire.

Dans la pratique, en hydrologie et en assainissement, on parle principalement de validation pour désigner le processus qui consiste à s'assurer qu'un modèle est capable de fournir des résultats acceptables pour une gamme donnée de phénomènes. On devrait, dans ce cas, plutôt parler de vérification. C'est uniquement cet aspect qui sera développé dans cet article et nous parlerons de façon équivalente de validation ou de vérification.

Nous raisonnerons dans le cadre des modèles opérationnels, construits pour atteindre un objectif spécifique. La démarche de vérification doit permettre dans ce cas de s'assurer que le modèle permet d'atteindre l'objectif fixé avec un niveau donné de confiance. Elle comprend trois étapes successives :

• choix du ou des critères permettant de préciser l'objectif à atteindre pour le modèle ;
• choix de l'écart acceptable sur chacun des critères pour vérifier le niveau de confiance attendu ;
• mise en œuvre de la démarche (reposant généralement sur l'acquisition et l’exploitation de données mesurées, si possible obtenues en continu, et/ou d’observations, par exemple de laisses de crues).

Choix du ou des critères

Considérations générales

Les modèles hydrologiques ou hydrauliques qui font l'objet de cet article peuvent être construits pour répondre à des objectifs très diversifiés. Les critères doivent donc être choisis en fonction des objectifs retenus. Sans prétendre à l'exhaustivité, nous illustrerons le choix des critères au travers de 3 exemples classiques :

• modèles destinés à représenter les crues majeures d'un cours d'eau ;
• modèles destinés à établir le diagnostic de fonctionnement hydraulique d'un réseau d'assainissement ;
• modèles destinés à représenter les rejets urbains de temps de pluie, par exemple dans le cadre de l'autosurveillance.

Quel que soit l'objectif, ces critères doivent présenter des qualités communes minimales :

• représentativité vis à vis des objectifs à atteindre ;
• mesurabilité ou capacité à être calculés à partir des données disponibles ;
• objectivité.

Dans tous les cas la méthode reposera généralement sur des campagnes de mesures permettant de comparer les valeurs calculées à partir des mesures et observations aux valeurs résultant des modélisations. Trois conditions importantes devront systématiquement être respectées :

• utiliser impérativement pour la vérification des "événements hydrologiques" différents de ceux ayant été utilisés pour le calage ;
• utiliser un nombre d'événements d'autant plus important que les incertitudes sur les mesures sont grandes (10 à 15 événements constitue un nombre minimum souhaitable qui, malheureusement, ne peut pas toujours être atteint) ;
• utiliser des événements hydrologiques représentatifs de ceux visés par les objectifs.

Cas des modèles destinés à représenter les crues majeures d'un cours d'eau

Ce type de modèle peut être construit spécifiquement pour un cours d'eau donné, voire pour une portion particulière de ce cours d'eau ou pour une classe particulière de cours d'eau. Dans ce cas on distingue en général la validation interne, c'est à dire la capacité du modèle à reproduire les crues sur les cours d'eau sur lesquels il a été calé, et la validation externe, c'est à dire sa capacité à reproduire des crues sur des cours d'eau non utilisés pour le calage.

Dans tous les cas on s'intéresse par définition à des événements rares. La probabilité d'observer une crue majeure dans un délai raisonnable après la construction du modèle est donc très faible. Les événements utilisables pour la vérification seront donc nécessairement des événements historiques. Ceci peut contraindre fortement les critères utilisables qui ne pourront reposer que sur les données disponibles. Les critères possibles seront généralement les mêmes que ceux utilisés pour le calage ; par ordre d'intérêt et pour différentes crues :

• le niveau d'eau maximum atteint en différents points d'intérêt (ce critère prime car l'évaluation correcte du risque d'inondation constitue généralement l'objectif principal) ;
• le débit maximum atteint en différents points d'intérêt ;
• le volume de la crue ;
• le temps de montée (important pour avertir les populations exposées) ;
• la forme de l'hydrogramme de crue (évaluable par exemple par le critère de Nash).

Cas des modèles destinés à établir le diagnostic de fonctionnement hydraulique d'un réseau d'assainissement

Les modèles de ce type utilisent généralement un logiciel générique spécifiquement adapté sur le réseau à étudier. Les logiciels disponibles (CANOE, Hydranet, InfoWorks, PCSWMM, ...), reposent sur des modélisations mathématiques assez voisines et sont tous parfaitement capables de représenter correctement le fonctionnement hydraulique d'un réseau d'assainissement complexe à deux conditions :

• avoir correctement décrit la structure physique du réseau et en particulier des ouvrages spéciaux comme les déversoirs d'orage ;
• avoir été correctement calés sur un nombre suffisant d'événements pluvieux représentatifs (en particulier incluant des pluies suffisamment fortes pour provoquer des dysfonctionnements du réseau).

Remplir ces deux conditions demande en général du temps et de la patience, ce qui explique que souvent on alterne les phases de calage et les phases de vérification.

Pour ce type de problème, les critères de validation possibles, également par ordre d'intérêt et pour différents événements, sont les suivants :

• comparaison des points de débordements simulés et observés ;
• volumes débordés par sous-bassins versants, par sous-réseaux ou par rue ;
• débits maximum à différents points d'intérêt.

Cas des modèles destinés à représenter les rejets urbains de temps de pluie, par exemple dans le cadre de l'autosurveillance

Comme pour le cas précédent, les modèles de ce type utilisent généralement un logiciel générique spécifiquement adapté sur le réseau à étudier. De la même façon on n'évalue donc pas vraiment la qualité du logiciel générique, supposée suffisante, mais celle de la représentation du réseau et celle du calage. La qualité de représentation des déversoirs d'orage est ici prépondérante.

Les critères possibles sont les suivants :

• volume totaux rejetés par les déversoirs d'orage sur une base de temps donnée (typiquement l'année), ceci par branche du réseau, ou par milieu récepteur, ou éventuellement par déversoir pour les plus importants d'entre eux ou si leur nombre total est réduit ;
• classement fréquentiel des volumes rejetés pendant une certaine période de temps (pluriannuelle) pour les événements les plus forts observés, ceci par branche du réseau, ou par milieu récepteur, ou éventuellement par déversoir pour les plus importants d'entre eux ;
• volumes individuels rejetés pour un ensemble représentatif de déversoirs et d'événements pluvieux.

Nota : pour les modèles de ce type il est intéressant d'utiliser pour le calage des hydrogrammes observés en différents points d'intérêt du réseau ; le fait que les critères de calage soient différents des critères de validation permet de conforter la confiance que l'on peut avoir dans le modèle.

Écarts acceptables sur les critères pour considérer le modèle comme validé

Considérations générales

Déterminer la valeur acceptable du critère d'écart suppose au préalable d'avoir déterminé les incertitudes sur :

• les éléments nécessaires au fonctionnement du modèle (incertitudes sur la connaissance de la pluie, sur la nature des surfaces, etc.) qui induisent des incertitudes sur la valeur des paramètres calculés utilisés pour déterminer le ou les critères (principalement volumes et/ou débits) ;
• la mesure directe des paramètres utilisées pour calculer le critère (par exemple la validité de la courbe de tarage pour déterminer les débits dans la gamme correspondant à ceux des évènements pris en référence.

Tout écart inférieur à l'incertitude sur cet écart est en effet non significatif. De fait, en première approximation, on peut considérer que l'écart acceptable entre les valeurs simulées et les valeurs calculées pour le critère choisi doit être de l'ordre de grandeur de la somme des incertitudes sur chacune des deux familles de valeurs.

Ces incertitudes sont souvent très importantes pour un événement particulier et un point particulier. Ceci explique pourquoi il est préférable de privilégier des critères intégrateurs pour lesquels les incertitudes sont plus faibles. Malgré tout, les deux familles d'incertitudes dépendent d'un grand nombre d'éléments locaux : par exemple densité du réseau de pluviomètres, utilisation éventuelle de données provenant d'un radar météorologique, qualité des mesures de débit, nombre d'événements utilisés, complexité du réseau, etc.. Il est donc extrêmement difficile de donner ne serait-ce que des ordres de grandeur des écarts acceptables, ce qui ne doit pas dispenser de le faire au mieux.

Exemple de validation

L'exemple traité ci-dessous correspond à la comparaison des flux journaliers mesurés et simulés entrant dans une station d'épuration. La figure 1 compare les volumes journaliers mesurés et simulés.

Figure 1 : volumes journaliers mesurés et simulés en entrée de la station d'épuration

Différents critères utilisables pour savoir si la simulation est correcte sont explicités ci dessous.

Volume total annuel

Le volume total annuel simulé est de 86 203m³ alors que le volume simulé est de 88 084m³. Les incertitudes sur les volumes mesurés sont évalués à 15%, et celles sur les volumes mesurés à 25%.

Vis à vis de ce critère, la simulation est donc excellente puisque l'écart de 2% est très inférieur aux incertitudes. Il est cependant possible que cette excellence cache de grosses différences qui se compensent sur l'année. Ce critère est donc insuffisant.

Écart quadratique moyen ou Critère de Nash calculés sur l'ensemble de la série

L'écart quadratique moyen est égal à la racine carrée de la somme des carrés des écarts divisée par le nombre de valeurs.

Dans ce cas il est égal à 5,1m³ pour une valeur moyenne journalière mesurée de 236m³; soit un écart relatif moyen qui est également de l'ordre de 2%.

Les hydrologues utilisent également souvent le critère de Nash-Sutcliffe qui s’écrit ;

Avec :

• $ S_{ob} $ et $ S_c $ : Valeurs observées et calculées au i^eme pas de temps ;
• $ Δt $ : pas de temps de la série chronologique discrétisée ;
• $ S_{mob} $ : moyenne arithmétique des observations.

La encore le critère de Nash, avec une valeur de $ 0{,}99 $, frise la perfection.

Cette excellence ne constitue cependant pas une preuve que le modèle soit lui-même excellent dans l'absolu. Elle indique seulement que le modèle est capable de discriminer correctement les jours de temps sec et les jours de pluie (ce qui constitue un minimum) et de représenter correctement l'ordre de grandeur des volumes journaliers produits par temps de pluie.

Écarts sur les valeurs extrêmes

Une autre façon de procéder, plus importante si on s'intéresse au temps de pluie et particulièrement aux situations rares, consiste à comparer les plus fortes valeurs simulées et observées.

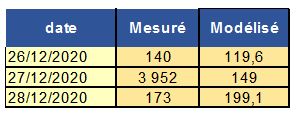
Si on recherche la plus forte valeur mesurée (3 952m³), on a alors une très mauvaise surprise. Celle-ci a été observée le 27 décembre comme le montre le tableau de la figure 2, et ce jour ci, la simulation produit une valeur 25 fois plus faible (149m³), correspondant à une journée de temps sec ordinaire. Le modèle semble donc totalement mis en défaut.

Figure 2 : Comparaison des volumes journaliers mesurés et simulés en entrée de la station d'épuration du 26 au 28 décembre.

Trois explications sont possibles :

• la simulation est totalement fausse ce jour particulier ;
• la mesure est totalement fausse ce jour particulier ;
• il s'est passé ce jour-ci un phénomène qui n'est pas pris en compte dans le modèle de simulation utilisé.

La première explication peut facilement être éliminée en constatant qu'il n'a pas plu ce jour ni le jour précédent et donc qu'aucune eau pluviale n'a été produite.

Différents phénomènes autres que la pluie peuvent provoquer des écoulements, par exemple une fonte de neige (qui n'est pas prise en compte par le modèle utilisé), la vidange d'une cuve ou d'une piscine, la rupture d'une conduite d'eau potable, etc.. Est-ce pour autant, au cas où l'une de ces explications soit la bonne, que le modèle doit être remis en cause ? Il est effectivement possible de doter le modèle de fonctions complémentaires, par exemple la prise en compte des stocks de neige et de leur fonte. Cependant jamais aucun modèle ne sera capable de prendre en compte un événement accidentel comme la rupture d'une conduite d'eau potable par exemple. Il faut donc accepter que dans certains cas des écarts importants existent entre les valeurs mesurées et les valeurs simulées. En revanche il est indispensable de déterminer les raisons de cet écart.

Ce critère doit donc également être utilisé avec prudence et tout écart important doit faire l'objet d'une analyse détaillée. Sa prise en considération montre cependant la limite des critères précédents qui n'avaient pas permis de détecter une différence très importante un jour particulier.

Analyse fréquentielle

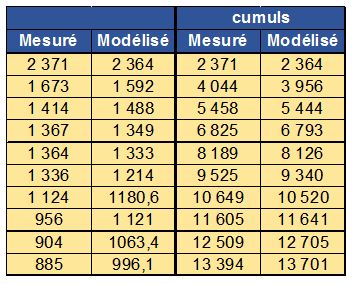
Pour éviter d'être piégé par une ou quelques valeurs extrêmes pouvant correspondre à des erreurs de mesure ou à des phénomènes parasites, il est préférable de travailler sur la comparaison des fréquences de dépassement des volume prévus et observés, ce qui correspond effectivement au résultat attendu pour l'autosurveillance. Pour ceci on "oublie" les dates où les événements se sont produits et on se contente de classer les valeurs mesurées et simulées par ordre décroissant conformément à la figure 3.

Figure 3 : Dix plus fortes valeurs mesurées et simulées classées par ordre décroissant.

En traçant les domaines d'incertitudes des valeurs mesurées et simulées (figure 4), on observe que les domaines d'incertitude se recouvrent, sauf pour la valeur la plus forte.

Figure 4 : Domaines d'incertitude des plus fortes valeurs mesurées et simulées classées par ordre décroissant.

On retrouve bien le résultat observé précédemment : la plus forte valeur mesurée correspond dans ce cas soit à une erreur de mesure, soit à un phénomène accidentel non pris en compte par le modèle, mais elle pourrait également correspondre à l'incapacité du modèle à représenter les événements les plus forts.

Si on retire cette valeur particulière, on met alors en évidence la très bonne capacité du modèle à reproduire les valeurs extrêmes.

Figure 5 : Comparaison des plus fortes valeurs mesurées et simulées classées par ordre décroissant après avoir enlevé la mesure particulière du 27 décembre

Méthode du double cumul

Il est possible d'améliorer encore la méthode précédente en travaillant non plus sur les valeurs elles-mêmes mais sur leurs cumuls (voir figure 6).

Figure 6 : Cumul des plus fortes valeurs mesurées et simulées classées par ordre décroissant après avoir enlevé la mesure particulière du 27 décembre

Le tracé de la courbe cumul des valeurs simulées fonction du cumul des valeurs observées fournit alors plusieurs informations sur la qualité de la simulation (voir figure 7).

Figure 7 : Cumul des plus fortes valeurs simulées fonction du cumul des valeurs mesurées.

• Le coefficient de corrélation proche de 1 indique que la relation est linéaire.
• Le coefficient directeur de la droite également proche de 1 indique que le volume simulé est proche du volume mesuré quel que soit l'importance de l'événement (du moins, dans l'exemple, pour les 10 plus forts).

Il est possible d'étudier le double cumul sur des plages beaucoup plus étendues, et même sur la totalité des valeurs (dans ce cas on retrouve également le critère de volume total annuel). Il est également possible d'effectuer le double cumul sur des valeurs classées de façon différentes. Par exemple un classement par date croissante pourrait permettre de mettre en évidence, par des ruptures de pente dans la courbe, une sous-estimation systématique des valeurs mesurées à certaines périodes de l'année et/ou une sur-estimation pendant d'autres périodes, etc.

Conclusions sur le choix des critères dans ce cas

Le cas présenté correspond à un modèle parfaitement calé par rapport aux mesures, beaucoup mieux que ce que l'on est le plus souvent capable de faire. Mais ceci ne garantit pas qu'il représente parfaitement la réalité : les résultats mesurés et simulés peuvent être faux tous les deux de la même façon ! Il est donc toujours nécessaire de rester vigilant et de diversifier les modes de contrôle et de validation (mesures en différents points, par différents dispositifs métrologiques, etc.).

Ceci dit cet exemple montre bien la nécessité, même dans un cas simple, de choisir les critères par rapport aux objectifs poursuivis et surtout celle de ne pas se contenter d'un critère unique.

Article en chantier

Voir aussi : Calage d’un modèle.