Modèle - généralités (HU)
Traduction anglaise : Model - general information
Dernière mise à jour : 12/04/2024
Avertissement au lecteur : Cet article ne traite pas du sens souvent attribué au mot "modèle" dans les études hydrologiques ou les études d'assainissement, mais essaie de préciser le contenu même du concept de modélisation. Pour avoir des informations plus spécifiques, voir les articles de la catégorie "Modélisation de la transformation pluie-débit (HU)" et l'article Modélisation en hydrologie et en hydraulique (généralités) (HU).
En théorie des systèmes : "un modèle est un schéma (description mentale intériorisée ou figurée par des diagrammes, des formules mathématiques, etc.) qui, pour un champ de questions, est pris comme représentation d'une classe de phénomènes, plus ou moins habilement dégagés de leur contexte par un observateur pour servir de support à l'investigation et/ou à la communication." (Roy, 1985).
Sommaire |
Sens usuel et sens scientifique
Venant du latin modulus qui signifie mesure ou mode, le mot "modèle" a pour définition usuelle : "ce qui est donné pour servir de référence" www.larousse.fr. On parle par exemple du modèle que le peintre essaie de reproduire. Cependant, dans le domaine scientifique, ce mot prend un sens totalement différent. Par exemple, si l'on reprend l'exemple du peintre, au sens scientifique retenu ici, c'est la peinture qui constitue le modèle alors que le sujet constitue l'objet à représenter!
Cette dualité a en fait été présente tout au long de l'histoire et, selon les différentes convictions philosophiques du moment, des définitions très variées et semblant parfois même contradictoires ont été proposées.
L'article de l’Encyclopédie Universalis, se propose d'éclairer l'origine de la notion de modèle par le langage de la philosophie et de montrer que cette dualité n'est pas nécessairement synonyme de contradiction.
Selon cet article l'origine du sens scientifique est technologique : "le modèle est d'abord la maquette, l'objet réduit et maniable qui reproduit en lui, sous une forme simplifiée, miniaturisée, les propriétés d'un objet de grandes dimensions, qu'il s'agisse d'une architecture ou d'un dispositif mécanique", c'est le sens que l'on donne aujourd'hui au modèle réduit.
Cette définition semble paradoxale car selon la conception platonicienne, le modèle était considéré comme un paradigme (une forme idéale sur laquelle les existences sont réglées). "Le modèle technique inverse donc la situation du modèle platonicien, puisqu'il est réalisation concrète au lieu d'être idée réalisable. Toutefois, la complexité de l'épistémologie autorise les glissements du sens. Il n'est pas interdit de concevoir que l'opération qui extrait d'une situation une figure de celle-ci permet en retour de fixer un type idéal et fournit un paradigme pour la reconstruction de cette situation. Ainsi, la physique de l'atome s'est développée autour du « modèle de Bohr », qui était d'abord une manière de schématiser les propriétés électriques de l'élément physique, d'unifier les effets spectraux des radiations qu'il émet. Au mieux, le modèle, dans les sciences évoluées, sert à fixer les lois sur un objet bien structuré, et cette fixation favorise à son tour la conception et l'expérimentation : les deux sens majeurs du terme de modèle, qui est une figuration et en même temps un schéma directeur, se recoupent et se conjuguent plus ou moins.'"
Il est donc logique que des conceptions intermédiaires soient proposées entre ces deux acceptions extrêmes. Selon Descartes par exemple, le modèle est une représentation du possible comme parabole destinée à suggérer les propriétés véritables des corps. Le modèle est donc à la fois source d’intuition et objet pédagogique permettant de comprendre le monde (Walliser, 1977).
Au XIXème siècle et selon le courant positiviste, le modèle est considéré comme une illustration fictive, un artifice utile mais provisoire d’une Théorie qui détient le vrai. L’hypothèse n’est pas "négociable", elle est dictée par les lois, la démarche est forcément déductive. "L’hypothèse physique, pour être jugeable doit exclusivement porter sur les lois des phénomènes et jamais sur leur production" (Comte, 1830).
Le modèle n’est alors qu’une forme dégradée d’une loi de la nature unique, vraie et universelle que l’on atteindra par la Théorie.
L’approche relativiste, qui s’est essentiellement développée en réaction au courant précédent, estime que le modèle marque des états traversés par une théorie qui est elle-même mouvante et évolutive. Ce courant considère implicitement que la théorie est astreinte à se modéliser.
"La vérité objective de la science échappe à tout regard scientifique puisqu’elle est ce regard" (Morin, 1986).
Cette définition est prolongée par l’approche systémique qui considère que toute production scientifique est acte de modélisation. "Nous arrivons ainsi à ce qui constitue la singularité de la science moderne : la rencontre entre la technique et la théorie, l’alliance systématique entre l’ambition de modeler le monde et celle de le comprendre" (Prigogine & Stengers, 1978). Dans cette conception de la science, la recherche du VRAI qui a conduit à considérer des problèmes de plus en plus pointus et qui a largement contribué à la parcellisation des savoirs est supplantée par un souci d’efficacité, et d’action sur le monde. Cette vision a mené à l'ouverture des problèmes scientifiques vers plus de globalité mais plus de complexité où la modélisation devient un outil privilégié permettant à la fois de représenter, d’analyser et d’agir :
"Un modèle n’est ni vrai, ni faux, le critère de comparaison des modèles est utilitaire : le meilleur étant celui qui fait du monde réel les prédictions les plus précises." (Feuvrier, 1971).
Classification des modèles
Les classifications des modèles sont nombreuses suivant les critères que l'on considère. Deux principales seront utilisées dans cet article : par type d'utilisation des modèles et par type d'approche.
Classification par type d'utilisation
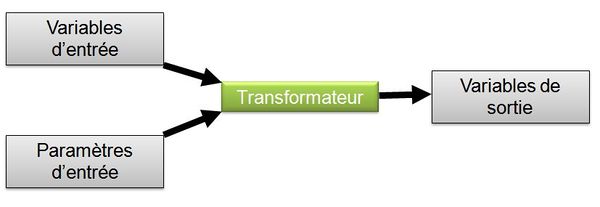
La classification retenue repose sur celle proposée par (Walliser, 1977). Elle consiste à représenter un modèle comme un transformateur d'informations qui produit des variables de sorties à partir de variables d'entrée et de paramètres (figure 1).
Par exemple pour un modèle hydrologique représentant un bassin versant ou un ouvrage :
- les variables d'entrée peuvent être la pluie ou plus généralement une séquence climatique ;
- les variables de sortie seront par exemple les valeurs de débit à l'exutoire du bassin versant ou la hauteur d'eau dans l'ouvrage ;
- les paramètres, pour leur part, caractériseront ce bassin versant (surface, pente, coefficient de ruissellement, etc.) ou cet ouvrage (dimensions, modalités de fonctionnement) ; dans le cas où le système étudié est un ouvrage, les paramètres pourront correspondre à des variables de conception à définir (par exemple le diamètre d'une conduite ou le volume d'un bassin de retenue).
A partir de ce schéma général, il est possible de déduire l'existence de trois catégories de modèles dont les objectifs peuvent parfaitement être ajustés à des familles de problèmes classiques rencontrés en hydrologie urbaine.
Nota : Cette typologie constitue elle-même une modélisation des différents types de modèles qui peut être rangée dans la catégorie des modèles cognitifs à but pédagogique ; elle est légèrement différente de celle proposée originellement par Walliser (1977).
Les modèles cognitifs : des modèles pour connaître, décrire ou comprendre
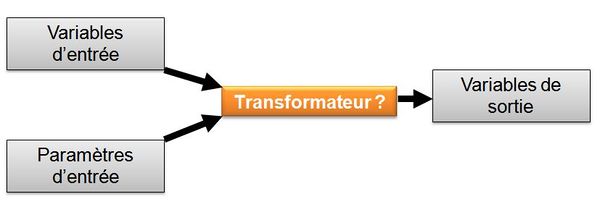
Dans cette catégorie, à partir de l'observation des variables d'entrée et de sortie ainsi que de celle des paramètres, on cherche à construire un transformateur permettant de mieux comprendre ou simplement de mieux décrire la façon dont fonctionne le système étudié (figure 2).
- S'il s'agit de mieux comprendre, l'idée générale est que le modèle permette de formuler des hypothèses complémentaires qui pourront ensuite être validées ou invalidées par une expérimentation (en changeant la valeur des paramètres et/ou celle des variables d'entrée) et en comparant les variables de sortie prévues et observées ; c'est le type de modèle qu'utilise les chercheurs.
- S'il s'agit simplement de mieux décrire, le modèle doit alors avoir un rôle pédagogique permettant par exemple de mieux expliquer l'importance d'un paramètre particulier.
Les modèles prévisionnels : des modèles pour prévoir et pour simuler
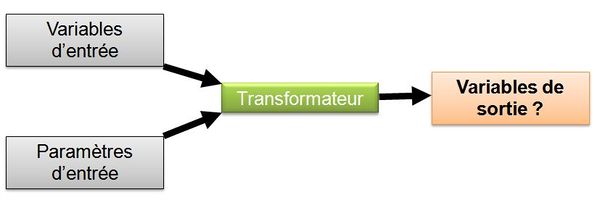
Les modèles de ce type ont pour objectif de prévoir le fonctionnement ou l'état d'un système : connaissant les variables d'entrée et les paramètres, ils doivent être capables de fournir une estimation utilisable des variables de sortie. Les modèles de simulation font partie de cette famille. En hydrologie, un modèle de ce type permettra par exemple de calculer la façon dont évolue le niveau d'eau dans un bassin de retenue (variable de sortie à déterminer) pour un événement pluvieux donné (variable d'entrée connue).
Nota : Les modèles de résolution du problème inverse (déconvolution par exemple) qui cherchent à déterminer les variables d'entrée ayant provoqué un jeu particulier de valeurs pour les variables de sortie peuvent soit être rattachés à cette catégorie, soit rattaché à la catégorie suivante (modèles décisionnels), soit constituer une catégorie à part.
Les modèles décisionnels : des modèles pour décider ou pour optimiser
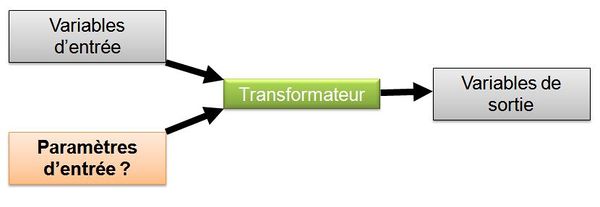
Ces modèles ont pour objectif de déterminer quelles sont certains des paramètres (variables de conception) à fournir au transformateur pour atteindre un objectif donné (variables de sortie imposées) dans un contexte particulier (variables d'entrée fixées) (figure 3). En hydrologie, un modèle de ce type permettra par exemple de calculer quel doit être le volume d'un bassin de retenue pour permettre de contrôler un événement pluvieux donné, correspondant par exemple à une période de retour fixée.
Nota Il est important de ne pas assimiler trop rapidement la nature du problème à la catégorie de modèle. En particulier un modèle prévisionnel peut parfaitement être utilisé pour résoudre un problème décisionnel. La résolution du problème ne sera alors plus directe et nécessitera la mise en œuvre d'une procédure itérative consistant à modifier progressivement les valeurs de paramètres jusqu'à ce que les variables de sortie obtenues soient conformes à celles attendues.
Classification selon l'approche de modélisation choisie
Il existe un grand nombre de classification des modèles. Dans la typologie proposée ci-dessous, seuls les critères de classification les plus courants ont été utilisés. Il faut noter que ces critères ne sont pas exclusifs les uns des autres.
Approches physique, symbolique ou analogique
- L’approche physique consiste à construire matériellement une représentation d’un objet. Les modèles réduits font partie des modèles physiques et ont pendant de longues années été utilisés pour modéliser le fonctionnement de futures constructions (barrage, station de pompage, etc.) ou pour simuler des équipements ou des milieux existants (écoulement de rivière, fonctionnement côtier, etc.).
- Les modèles symboliques utilisent pour leur part un langage abstrait. Ce peut être un schéma ou un dessin, mais les modèles symboliques aujourd'hui de loin les plus utilisés sont ceux qui reposent sur la représentation des phénomènes par des équations mathématiques. Voir modèles mathématiques.
- Les modèles analogiques sont fondés sur l’identité de fonctionnement d’objets ou de processus pris dans des champs disciplinaires différents. Par exemple, l’écoulement de l’eau dans un barrage en terre peut être représenté par une analogie électrique. En effet dans un milieu isotrope, le potentiel "charge électrique" d'un milieu conducteur homogène joue le rôle du potentiel "charge hydraulique" dans un milieu poreux, la densité de courant le rôle de la vitesse de décharge de l'eau et enfin la conductibilité électrique celui du coefficient de perméabilité. Les modèles analogiques peuvent être utilisés sous une forme mathématiques ou constituer une forme particulière de modèle physique. La résolution pratique d'un certain nombre de problèmes d'écoulement à deux dimensions a par exemple pu être facilitée par l'utilisation de modèles réduits électriques.
Approche axiomatique ou heuristique
- L'approche axiomatique consiste à définir des principes, des hypothèses et des règles stricts, clairement explicités, qui seront exploités de manière déductive.
- L'approche heuristique consiste selon (Walliser, 1977), "à réunir des propositions partielles sur un système, formellement hétérogènes et s'articulant de façon approximative, mais introduisant des conceptions plus nuancées et des rapports plus réalistes que la précédente". De façon pratique, un modèle fondé sur une approche heuristique permet généralement de trouver une solution au problème mais sans que l'on soit capable de démontrer rigoureusement les raisons pour lesquelles le modèle fonctionne ni pouvoir garantir qu'il fonctionnera toujours. Les modèles fondés sur une approche axiomatique sont donc a priori plus rigoureux que ceux fondés sur une approche heuristique au sens où ils sont plus facilement démontrables.
Dans le domaine très complexe de l'hydrologie et de l'assainissement les connaissances sont le plus souvent incomplètes et de nature qualitative. Les approches strictement axiomatiques sont donc difficiles à mettre en place sans négliger une partie importante de la complexité du problème et surtout des connaissances empiriques disponibles. La plupart des modèles ressortent donc d'une approche au moins en partie heuristique.
Approche déterministe ou probabiliste
- Dans un modèle déterministe, les paramètres, les variables d'entrée et de sortie décrivant un système ou son fonctionnement, ainsi que les équations qui les relient sont parfaitement déterminés ou déterminables : une même cause produit toujours le même effet. L'une de leur propriété est qu'ils sont réversibles : connaissant l'effet les mêmes équations permettent de remonter aux causes.
- Dans un modèle probabiliste ou stochastique, on considère que les variables d'entrée et de sortie, voire les paramètres, peuvent être modélisés par autre chose que des valeurs certaines. On fait l'hypothèse que l'on peut associer à chaque grandeur incertaine, un nombre fini ou infini de valeurs probables auxquelles sont attachées une probabilité ou une loi de probabilité. L'approche probabiliste est utilisée, soit parce que le phénomène étudié est aléatoire, ou du moins considéré comme tel (c'est le cas de la modélisation des pluies), soit parce que l'on cherche à représenter des permanences difficilement explicitables physiquement (lois très complexes faisant intervenir beaucoup de paramètres par exemple) ou enfin pour associer une incertitude à un résultat.
Approche microscopique (réductionniste) ou approche macroscopique (holistique, globale)
- L'approche microscopique ou réductionniste consiste à décomposer un système et son fonctionnement en "sous-systèmes" supposés élémentaires et en "micro phénomènes", de les modéliser tous avec soin et de construire ensuite un modèle de recomposition ; les modèles hydrologiques de ce type sont par exemple les modèles distribués.
- L'approche macroscopique ou holistique, ou encore globale, considère le système dans son ensemble et s'intéresse uniquement à son comportement global. Voir Modèle global.
En hydrologie la très grande diversité des échelles physiques à prendre en compte, la diversité des phénomènes et leurs interactions font que le modèle représentant les phénomènes à l'échelle la plus fine reste un modèle global.
Approche théorique, conceptuelle ou empirique
- L'approche théorique s'appuie sur l'abstraction et sur le raisonnement ; les modèles fondés sur ce principe sont construits a priori, l'expérience pouvant venir ensuite pour le conforter, le valider ou le caler. On parle de modèle mécaniste, ou de façon plus générale de Modèle à base physique.
- L'approche empirique est fondée sur l'exploitation de l'expérience et des constations qui en découlent ; les modèles empiriques sont limités dans la mesure où il y a extrapolation de constations faites sur des expérimentations dont la reproductibilité est toujours source de questionnements. Voir modèle empirique.
- L'approche conceptuelle vise à représenter le fonctionnement d'un système à l'aide d'un concept simple, facilement appréhendable, choisi plus ou moins a priori et ne reposant pas sur les lois physiques régissant les processus concernés ; on parle également souvent de modèles de type « boite noire ». Voir modèle conceptuel.
En hydraulique on utilise des modèles dit à base physique fondés sur une approche théorique (voir Mécanique des fluides numérique / MFN (HU)). On est cependant la plupart du temps à faire des hypothèses très simplificatrices qui réduisent l'intérêt de l'approche (voir Barré de Saint Venant (équations de) (HU)).
En hydrologie la plupart des modèles reposent sur des approches empiriques ou conceptuelles. La différence entre modèle empirique et modèle conceptuel est d'ailleurs floue et ne repose que sur la façon dont le modèle a été élaboré. Dans le premier cas on part des observations et on cherche, en théorie sans idée préconçue, une relation (généralement sous la forme d'une relation mathématique) entre les entrées et les sorties observées. Dans le second cas on postule a priori l'existence d'une relation prenant une certaine forme, conforme au concept choisi, et on utilise les données d'observation pour caler au mieux les paramètres du modèle ainsi élaboré.
Les deux approches peuvent conduire à des formulations strictement identiques et il n'est pas toujours simple, même pour le concepteur du modèle, de savoir exactement les raisons qui ont guidé vers le choix d'une forme particulière de relation.
Critères de qualité d'un modèle
Le choix d'un modèle pour résoudre un problème particulier nécessite de s'appuyer sur un certain nombre de critères permettant de juger de la capacité du modèle à fournir les informations adéquates. Les principaux critères utilisables pour juger de la qualité d'un modèle sont présentés ci-dessous.
Pertinence
Un modèle sera pertinent, si pour le champ de questions auquel il est censé répondre :
- il est capable de reproduire les phénomènes étudiés ;
- il donne de "bons résultats", correspondant en particulier à la précision attendue,
- il fournit ses résultats sous la forme attendue.
Robustesse
La robustesse d'un modèle caractérise son aptitude à ne pas diverger numériquement lorsque les entrées sont modifiées (en particulier faible sensibilité aux conditions aux limites). En hydrologie, il est indispensable que les modèles soient robustes, de telle manière que si on modifie légèrement un paramètre d'entrée connu avec incertitude, ce qui est souvent le cas, les sorties varient peu.
Sensibilité
La sensibilité d’un modèle caractérise sa capacité a bien représenter la variation de certaines entrées particulièrement influantes. Un modèle doit absolument être sensible aux variations des grandeurs dont on cherche à simuler les effets ou que l’on cherche à dimensionner. Voir Sensibilité (études de).
Généricité
Si un modèle peut s'appliquer à un champ de questions très large, et fonctionne sans condition spéciale, il est dit générique, sinon il est dit adapté (sous-entendu à un contexte particulier). La généricité d'un modèle est importante car elle permet de traiter des questions diverses et sur des territoires différents.
Qualités pragmatiques
Les qualités pragmatiques recouvrent un ensemble de critères qui ne sont pas déterminants en terme de qualité des résultats fournis, mais qui caractérisent la plus ou moins grande facilité avec laquelle le modèle peut être utilisé. Les plus importantes sont les suivantes (Walliser, 1977) :
- la maniabilité : le modèle est simple à utiliser et ne présente aucune difficulté théorique (paramètres d'entrées difficiles à obtenir par exemple) ou pratique (mode de saisie des données très lourd) ;
- la transparence : caractérise l'aptitude du modèle à être compris d'un grand nombre de personnes (et en particulier de ses utilisateurs !) ;
- la souplesse : mesure la facilité avec laquelle il est possible de changer les données du modèle ;
- la qualité pédagogique : mesure la capacité d'un modèle à servir de support de communication et de dialogue entre différents acteurs ; un modèle pédagogique doit permettre de tirer facilement des enseignements sur le domaine étudié.
Bibliographie :
- Comte, A. (1830) : Cours de philosophie positive, tome 1, Paris, 1ère leçon.
- Feuvrier, C. V. (1971) : La simulation des systèmes ; Ed. Dunod, Paris.
- Morin, E. (1986) : La connaissance de la connaissance ; Ed. du Seuil ; Paris.
- Prigogine, I., Stengers, I. (1978) : La Nouvelle alliance, 1978, I, 4, Folio essais, 1986, p. 76-79.
- Roy, B. (1985) : Méthodologie multicritère d’aide à la décision ; Ed. Economica ; Paris.
- Walliser, B. (1977) : Systèmes et modèles ; Ed. du Seuil ; Paris.
 S'abonner à un flux RSS
S'abonner à un flux RSS