C.06 - Approches bayésiennes : Différence entre versions
(Page créée avec « == Introduction == Cette fiche vise seulement à introduire le principe des approches bayésiennes, à expliciter la terminologie usuelle qui leur est propre et à indiqu... ») |
(→Formalisme) |
||
| Ligne 15 : | Ligne 15 : | ||
Les approches bayésiennes décrivent notre connaissance de l'incertitude par des densités de probabilité. Nos connaissances sur le système étudié sont exprimées par la vraisemblance des données, qui est la densité décrivant la probabilité d'une observation Xt = x, étant donnée notre connaissance du système (notre modèle). | Les approches bayésiennes décrivent notre connaissance de l'incertitude par des densités de probabilité. Nos connaissances sur le système étudié sont exprimées par la vraisemblance des données, qui est la densité décrivant la probabilité d'une observation Xt = x, étant donnée notre connaissance du système (notre modèle). | ||
| + | Le théorème de Bayes [2] décrit une relation entre probabilités conditionnelles (P(A|B)): la probabilité de A sachant B est la probabilité d'un événement A étant donné une information B, fiche 1.08). Cette relation [3] s'écrit : | ||
| + | <center> | ||
| + | [[File:Inc244.bmp|250px]] | ||
| + | </center> | ||
| + | Ce théorème simple permet donc l'estimation de l'incertitude après prise en compte de la nouvelle observation B, appelée distribution a posteriori, ou encore posterior (P(A|B)), à partir de son estimation avant prise en compte, appelée distribution a priori ou prior (P(A))et la vraisemblance de l'observation B en question (probabilité de B connaissant A : P(B|A). | ||
| − | [1] | + | |
| + | |||
| + | Dans le cadre d'un système de prévision : | ||
| + | * P(A) est l'estimation initiale de l'incertitude sur la variable à prévoir X : Px(X) | ||
| + | * P(A|B) est alors l'estimation après prise en compte de l'information B (qui sera pour nous une observation Obs de débit ou de hauteur): Px(X|Obs) | ||
| + | * P(B|A) est la vraisemblance [4] de l'information B étant donné notre connaissance (le modèle M): [[File:Inc245.bmp|100px]] | ||
| + | |||
| + | |||
| + | |||
| + | L'équation 1. peut donc être réécrite en : | ||
| + | |||
| + | <center> | ||
| + | [[File:Inc246.bmp|350px]] | ||
| + | </center> | ||
| + | |||
| + | |||
| + | où le symbole [[File:Inc249.bmp|20px]] indique la proportionnalité [5]. | ||
| + | |||
| + | |||
| + | L’équation précédente peut alors être appliquée de façon itérative. L’apport de la n+1e observation est alors donné par : | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [1] Il s'agit ici de notre connaissance du bassin versant ou du réseau hydrographique que nous avons transcrite dans un modèle qui peut être validé (totalement ou partiellement) mais reste en tout état de cause un ensemble d'hypothèses de travail. | ||
| + | |||
| + | [2] Bayes était un mathématicien anglais de la première partie du XVIIIe siècle. | ||
| + | |||
| + | [3] Ce théorème vient du fait que [[File:Inc247.bmp|250px]] | ||
| + | |||
| + | [4] Vraisemblance se dit likelihood en anglais, ce qui explique qu'elle soit souvent notée par la lettre [[File:Inc248.bmp|20px]]. | ||
[[Catégorie:Incertitudes]] | [[Catégorie:Incertitudes]] | ||
Version du 5 septembre 2014 à 10:23
Sommaire |
Introduction
Cette fiche vise seulement à introduire le principe des approches bayésiennes, à expliciter la terminologie usuelle qui leur est propre et à indiquer certains points-clefs et difficultés. Il est impossible en quelques pages de décrire en détails l'ensemble de ces méthodes et de leurs emplois dans le domaine de la prévision.
Principe
Au lieu d'acquérir une connaissance de l'incertitude sur la base d'un ensemble de prévisions passées (fiche 3.07), les approches bayésiennes proposent de faire évoluer notre estimation de l'incertitude dès qu'une nouvelle information est disponible, c'est-à-dire pour nous prévisionnistes, dès qu'une nouvelle observation arrive, qui peut être mise en regard avec les prévisions faites pour cet événement.
Ces approches se fondent sur le théorème de Bayes qui décrit comment transformer notre connaissance avant l'apport d'information contenue par une observation en une connaissance enrichie tenant compte de cette information. Chaque nouvelle information est elle-même évaluée à partir de notre connaissance du fonctionnement du système étudié [1] (ou de nos hypothèses sur ce système).
Formalisme
Relation de Bayes
Les approches bayésiennes décrivent notre connaissance de l'incertitude par des densités de probabilité. Nos connaissances sur le système étudié sont exprimées par la vraisemblance des données, qui est la densité décrivant la probabilité d'une observation Xt = x, étant donnée notre connaissance du système (notre modèle).
Le théorème de Bayes [2] décrit une relation entre probabilités conditionnelles (P(A|B)): la probabilité de A sachant B est la probabilité d'un événement A étant donné une information B, fiche 1.08). Cette relation [3] s'écrit :
Ce théorème simple permet donc l'estimation de l'incertitude après prise en compte de la nouvelle observation B, appelée distribution a posteriori, ou encore posterior (P(A|B)), à partir de son estimation avant prise en compte, appelée distribution a priori ou prior (P(A))et la vraisemblance de l'observation B en question (probabilité de B connaissant A : P(B|A).
Dans le cadre d'un système de prévision :
- P(A) est l'estimation initiale de l'incertitude sur la variable à prévoir X : Px(X)
- P(A|B) est alors l'estimation après prise en compte de l'information B (qui sera pour nous une observation Obs de débit ou de hauteur): Px(X|Obs)
- P(B|A) est la vraisemblance [4] de l'information B étant donné notre connaissance (le modèle M):
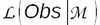
L'équation 1. peut donc être réécrite en :
où le symbole ![]() indique la proportionnalité [5].
indique la proportionnalité [5].
L’équation précédente peut alors être appliquée de façon itérative. L’apport de la n+1e observation est alors donné par :
[1] Il s'agit ici de notre connaissance du bassin versant ou du réseau hydrographique que nous avons transcrite dans un modèle qui peut être validé (totalement ou partiellement) mais reste en tout état de cause un ensemble d'hypothèses de travail.
[2] Bayes était un mathématicien anglais de la première partie du XVIIIe siècle.
[3] Ce théorème vient du fait que ![]()
[4] Vraisemblance se dit likelihood en anglais, ce qui explique qu'elle soit souvent notée par la lettre ![]() .
.
 S'abonner à un flux RSS
S'abonner à un flux RSS