Incertitude (HU) : Différence entre versions
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Uncertainty'' | ''<u>Traduction anglaise</u> : Uncertainty'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 05/04/2022 |
| − | Marge de variabilité possible de la survenue d’un événement ou de la valeur d’une grandeur | + | Marge de variabilité possible de la survenue d’un événement ou de la valeur d’une grandeur. |
| − | == | + | ==Signification statistique== |
| − | + | Du point de vue statistique, une incertitude est une variable aléatoire dont la distribution de probabilité peut être connue ou non. | |
| − | + | ==Importance de la notion d'incertitude en hydrologie urbaine== | |
| + | En hydrologie urbaine, la notion d’incertitude intervient dans trois domaines principaux où elle doit impérativement être prise en compte : | ||
| + | * En métrologie : la variabilité des phénomènes et la difficulté à les mesurer ''in situ'' font qu’il est toujours nécessaire d’attacher une incertitude, parfois grande, aux mesures effectuées ; | ||
* En [[Modélisation (HU)|modélisation ]]: la complexité des systèmes d’assainissement et des phénomènes qui s’y déroulent rendent également illusoire une représentation numérique qui serait à la fois précise et certaine. Une incertitude, également importante, doit donc être attachée aux résultats de modélisation ; | * En [[Modélisation (HU)|modélisation ]]: la complexité des systèmes d’assainissement et des phénomènes qui s’y déroulent rendent également illusoire une représentation numérique qui serait à la fois précise et certaine. Une incertitude, également importante, doit donc être attachée aux résultats de modélisation ; | ||
| − | + | * En gestion de [[Risque (HU)|risque]] : l'incertitude est principalement liée au fait que l'on s'intéresse à la prévision du futur en s’appuyant sur des données du passé ; l’incertitude résulte à la fois de la variabilité et de l'instabilité du phénomène dont on veut se protéger et des défauts dans les données utilisées pour effectuer les statistiques. | |
| − | * En gestion de [[Risque (HU)|risque]] : l'incertitude est liée au fait | + | |
==Prise en compte des incertitudes dans le calage des modèles== | ==Prise en compte des incertitudes dans le calage des modèles== | ||
| Ligne 19 : | Ligne 20 : | ||
Depuis l’apparition de la modélisation en hydrologie urbaine, et au vu des exigences de plus en plus fortes que demandent le [[Calage d'un modèle (HU)|calage]] des modèles, des discussions ont régulièrement divisé les métrologues et les modélisateurs concernant la source principale des écarts entre mesures et résultats des simulations. Il est en effet difficile de quantifier la part des incertitudes imputables aux unes et aux autres, d’autant qu’une troisième source importante existe : les approximations dans la description des caractéristiques des ouvrages, souvent assez mal connus du fait de leur caractère habituellement souterrain et des faiblesses de la documentation sur leur réalisation. | Depuis l’apparition de la modélisation en hydrologie urbaine, et au vu des exigences de plus en plus fortes que demandent le [[Calage d'un modèle (HU)|calage]] des modèles, des discussions ont régulièrement divisé les métrologues et les modélisateurs concernant la source principale des écarts entre mesures et résultats des simulations. Il est en effet difficile de quantifier la part des incertitudes imputables aux unes et aux autres, d’autant qu’une troisième source importante existe : les approximations dans la description des caractéristiques des ouvrages, souvent assez mal connus du fait de leur caractère habituellement souterrain et des faiblesses de la documentation sur leur réalisation. | ||
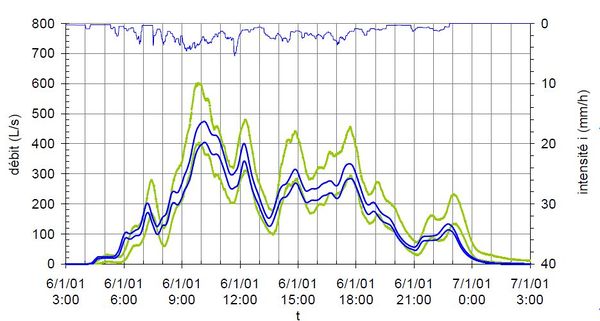
| − | [[File:incertitude.JPG|600px|center|thumb|<center>''Comparaison des débits simulés et mesurés avec un intervalle de confiance de 95% ; <u>Source</u> : [https://www.graie.org/othu/pdfothu/fiches/F2.pdf Fiche OTHU].''</center>]] | + | |
| + | [[File:incertitude.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Comparaison des débits simulés et mesurés avec un intervalle de confiance de 95% ; <u>Source</u> : [https://www.graie.org/othu/pdfothu/fiches/F2.pdf Fiche OTHU].''</center>]] | ||
En tout état de cause il serait souvent très utile d'associer une intervalle de confiance à tout résultat de calcul ou de simulation ainsi qu'à toute mesure. | En tout état de cause il serait souvent très utile d'associer une intervalle de confiance à tout résultat de calcul ou de simulation ainsi qu'à toute mesure. | ||
Version du 5 avril 2022 à 10:33
Traduction anglaise : Uncertainty
Dernière mise à jour : 05/04/2022
Marge de variabilité possible de la survenue d’un événement ou de la valeur d’une grandeur.
Signification statistique
Du point de vue statistique, une incertitude est une variable aléatoire dont la distribution de probabilité peut être connue ou non.
Importance de la notion d'incertitude en hydrologie urbaine
En hydrologie urbaine, la notion d’incertitude intervient dans trois domaines principaux où elle doit impérativement être prise en compte :
- En métrologie : la variabilité des phénomènes et la difficulté à les mesurer in situ font qu’il est toujours nécessaire d’attacher une incertitude, parfois grande, aux mesures effectuées ;
- En modélisation : la complexité des systèmes d’assainissement et des phénomènes qui s’y déroulent rendent également illusoire une représentation numérique qui serait à la fois précise et certaine. Une incertitude, également importante, doit donc être attachée aux résultats de modélisation ;
- En gestion de risque : l'incertitude est principalement liée au fait que l'on s'intéresse à la prévision du futur en s’appuyant sur des données du passé ; l’incertitude résulte à la fois de la variabilité et de l'instabilité du phénomène dont on veut se protéger et des défauts dans les données utilisées pour effectuer les statistiques.
Prise en compte des incertitudes dans le calage des modèles
Depuis l’apparition de la modélisation en hydrologie urbaine, et au vu des exigences de plus en plus fortes que demandent le calage des modèles, des discussions ont régulièrement divisé les métrologues et les modélisateurs concernant la source principale des écarts entre mesures et résultats des simulations. Il est en effet difficile de quantifier la part des incertitudes imputables aux unes et aux autres, d’autant qu’une troisième source importante existe : les approximations dans la description des caractéristiques des ouvrages, souvent assez mal connus du fait de leur caractère habituellement souterrain et des faiblesses de la documentation sur leur réalisation.
En tout état de cause il serait souvent très utile d'associer une intervalle de confiance à tout résultat de calcul ou de simulation ainsi qu'à toute mesure.
 S'abonner à un flux RSS
S'abonner à un flux RSS