Colebrook (formule de) (HU) : Différence entre versions
(→Choix des paramètres) |
|||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Colebrook's formula'' | ''<u>Traduction anglaise</u> : Colebrook's formula'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 13/11/2022 |
Formule, appelée parfois formule de Colebrook-White, initialement développée pour calculer les [[Perte de charge linéaire (HU)|pertes de charge linéaires]] dans le cas des écoulements en charge ; cette formule permet également d'évaluer le paramètre <math>C</math> de l'équation de [[Chézy (formule de) (HU)|Chézy]]. | Formule, appelée parfois formule de Colebrook-White, initialement développée pour calculer les [[Perte de charge linéaire (HU)|pertes de charge linéaires]] dans le cas des écoulements en charge ; cette formule permet également d'évaluer le paramètre <math>C</math> de l'équation de [[Chézy (formule de) (HU)|Chézy]]. | ||
| Ligne 20 : | Ligne 20 : | ||
avec : | avec : | ||
| − | |||
* <math>λ</math> : coefficient de Colebrook (sans dimension) ; | * <math>λ</math> : coefficient de Colebrook (sans dimension) ; | ||
* <math>g</math> : accélération de la pesanteur (m/s<sup>2</sup>) ; | * <math>g</math> : accélération de la pesanteur (m/s<sup>2</sup>) ; | ||
| Ligne 26 : | Ligne 25 : | ||
* <math>R_h</math> : [[Rayon hydraulique (HU)|rayon hydraulique]] (m) ; | * <math>R_h</math> : [[Rayon hydraulique (HU)|rayon hydraulique]] (m) ; | ||
* <math>ν</math> : [[Viscosité cinématique (HU)|viscosité cinématique]] du fluide (m<sup>2</sup>/s) ; | * <math>ν</math> : [[Viscosité cinématique (HU)|viscosité cinématique]] du fluide (m<sup>2</sup>/s) ; | ||
| − | * <math>a</math> et <math>b</math> : | + | * <math>a</math> et <math>b</math> : coefficients sans dimension (12 < <math>a</math> < 15 et 0 < <math>b</math> < 6). |
Les pertes de charge linaires se calculent par la relation générale : | Les pertes de charge linaires se calculent par la relation générale : | ||
| Ligne 34 : | Ligne 33 : | ||
| − | Pour un écoulement à surface libre, en régime uniforme, la pente de la ligne d'énergie est parallèle à la pente du fond, ce qui implique <math>I = J</math>. On peut donc écrire : | + | Pour un écoulement à surface libre, en régime uniforme, la pente de la [[Ligne d'énergie (HU)|ligne d'énergie]] est parallèle à la pente du fond, ce qui implique <math>I = J</math>. On peut donc écrire : |
<center><math>I = λ.\dfrac{V^2}{8.g.R_h} \quad\quad \Longrightarrow \quad\quad \dfrac{1}{\sqrt{\lambda}} = \dfrac{V}{\sqrt{8.g.R_h.I}} \quad(4)</math> </center> | <center><math>I = λ.\dfrac{V^2}{8.g.R_h} \quad\quad \Longrightarrow \quad\quad \dfrac{1}{\sqrt{\lambda}} = \dfrac{V}{\sqrt{8.g.R_h.I}} \quad(4)</math> </center> | ||
| − | |||
| Ligne 51 : | Ligne 49 : | ||
| − | <center><math>V = \dfrac{1}{\sqrt{λ}}.\sqrt{8. | + | <center><math>V = \dfrac{1}{\sqrt{λ}}.\sqrt{8.g.R_h.I} = C.\sqrt{R_h.I} \quad(6)</math> </center> |
| Ligne 61 : | Ligne 59 : | ||
En reportant la relation (5) dans l'expression (7), on obtient finalement une expression explicite du coefficient <math>C</math> de Chezy : | En reportant la relation (5) dans l'expression (7), on obtient finalement une expression explicite du coefficient <math>C</math> de Chezy : | ||
| − | |||
<center><math>C = -4\sqrt{2.g}.log \left(\frac{k}{a.R_h}+\frac{b.ν}{8.R_h\sqrt{2.g.R_h.I}}\right) \quad(8)</math></center> | <center><math>C = -4\sqrt{2.g}.log \left(\frac{k}{a.R_h}+\frac{b.ν}{8.R_h\sqrt{2.g.R_h.I}}\right) \quad(8)</math></center> | ||
| + | |||
==Choix des paramètres== | ==Choix des paramètres== | ||
| Ligne 73 : | Ligne 71 : | ||
* <math>b</math> = 2,51 | * <math>b</math> = 2,51 | ||
| − | Le tableau de la ''figure 1'' donne des indications sur le choix de <math>k</math> et : | + | Le tableau de la ''figure 1'' donne des indications sur le choix de <math>k</math> et de <math>ν</math> : |
| Ligne 83 : | Ligne 81 : | ||
==Lien avec la formule de Manning-Strickler== | ==Lien avec la formule de Manning-Strickler== | ||
| − | En élargissant l'application de la formule (9), proposée par Strickler pour le cas des canaux en terre ou avec des fonds sableux et valable pour les écoulements turbulents rugueux, au cas des conduites d'assainissement (Hager, 1999), on peut construire le tableau de la ''figure 2'' établissant un lien entre le coefficient <math> | + | En élargissant l'application de la formule (9), proposée par Strickler pour le cas des canaux en terre ou avec des fonds sableux et valable pour les écoulements turbulents rugueux, au cas des conduites d'assainissement (Hager, 1999), on peut construire le tableau de la ''figure 2'' établissant un lien entre le coefficient <math>K_s</math> de la [[Manning-Strickler (formule de) (HU)|formule de Manning-Strickler]] et la rugosité <math>k</math> de la formule de Colebrook. |
<center><math>K_s = 26.\left[\frac{1}{k}\right]^{1/6}\quad (9)</math></center> | <center><math>K_s = 26.\left[\frac{1}{k}\right]^{1/6}\quad (9)</math></center> | ||
| + | |||
avec : | avec : | ||
Version du 13 novembre 2022 à 15:53
Traduction anglaise : Colebrook's formula
Dernière mise à jour : 13/11/2022
Formule, appelée parfois formule de Colebrook-White, initialement développée pour calculer les pertes de charge linéaires dans le cas des écoulements en charge ; cette formule permet également d'évaluer le paramètre $ C $ de l'équation de Chézy.
Formulation mathématique
Sous sa forme originale, l'équation de Colebrook s'écrit :
Dans cette relation, $ R_e $ est le nombre de Reynolds :
avec :
- $ λ $ : coefficient de Colebrook (sans dimension) ;
- $ g $ : accélération de la pesanteur (m/s2) ;
- $ k $ : rugosité des parois (m) ;
- $ R_h $ : rayon hydraulique (m) ;
- $ ν $ : viscosité cinématique du fluide (m2/s) ;
- $ a $ et $ b $ : coefficients sans dimension (12 < $ a $ < 15 et 0 < $ b $ < 6).
Les pertes de charge linaires se calculent par la relation générale :
Pour un écoulement à surface libre, en régime uniforme, la pente de la ligne d'énergie est parallèle à la pente du fond, ce qui implique $ I = J $. On peut donc écrire :
En reportant les expressions (2) et (4) dans la relation (1), on obtient une formulation explicite de $ λ $ :
La relation (4) permet également d'écrire :
avec
En reportant la relation (5) dans l'expression (7), on obtient finalement une expression explicite du coefficient $ C $ de Chezy :
Choix des paramètres
Les valeurs généralement retenues pour $ a $ et $ b $ sont les suivantes :
- $ a $ = 14,8
- $ b $ = 2,51
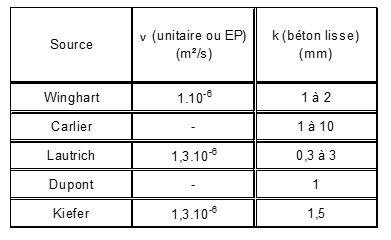
Le tableau de la figure 1 donne des indications sur le choix de $ k $ et de $ ν $ :
Généralement une valeur de $ k $ comprise entre 1,5 et 3 mm est acceptable pour des conduites en bon état non encombrées. Il est important de préciser que la rugosité des parois doit tenir compte, non seulement de la dimension des aspérités, mais également des macro-obstacles à l'écoulement que l'on peut rencontrer dans les systèmes d’assainissement : coudes, chutes, câbles accrochés aux parois, etc.
Lien avec la formule de Manning-Strickler
En élargissant l'application de la formule (9), proposée par Strickler pour le cas des canaux en terre ou avec des fonds sableux et valable pour les écoulements turbulents rugueux, au cas des conduites d'assainissement (Hager, 1999), on peut construire le tableau de la figure 2 établissant un lien entre le coefficient $ K_s $ de la formule de Manning-Strickler et la rugosité $ k $ de la formule de Colebrook.
avec :
- $ k $ : rugosité des parois au sens de Nikuradze (m) ;
- $ Ks $ : coefficient de Manning-Strickler (m1/3/s).
Bibliographie :
- Carlier, M. (1972) : Hydraulique générale et appliquée ; Eyrolles ; Paris ; 565 p. ; 1972.
- Lautrich, R. (1971) : Tables et abaques pour le calcul hydraulique des canalisations sous pression, égouts et caniveaux ; Eyrolles ; 1971.
- Hager, W. H. (1999) : Wastewater hydraulics: theory and practice ; Springer.
- Winghart, M. : Cours polycopié de mécanique des fluides et d'hydraulique ; INSA de Lyon - département GCU ; non daté.
Voir aussi : Coefficient de rugosité, Perte de charge.
 S'abonner à un flux RSS
S'abonner à un flux RSS