Méthode des pluies (HU)

Traduction anglaise : Rainfalls design method

Dernière mise à jour : 3/2/2020

Cette méthode, connue aussi sous le nom de méthode hollandaise, permet de dimensionner facilement les volumes des ouvrages de stockage (bassins de retenue).

Hypothèses de départ

Dans sa formulation classique, la méthode suppose :

• que le débit de fuite $ Q_v $ de l'ouvrage de stockage est constant ;
• que le coefficient d'apport $ C_a $ est indépendant de la pluie ;
• qu’il y a transfert instantané de la pluie à l'ouvrage de stockage, c'est à dire que les phénomènes d'amortissement dus au ruissellement sur le bassin sont négligés.

Les conséquences de ces hypothèses ainsi que leur incidence sur le résultat est discutée plus bas.

Attention : Les unités utilisées dans cet article sont les unités SI et ne correspondent pas aux unités usuelles pour lesquelles on fournit classiquement les coefficients de Montana (durées en minutes, hauteurs d'eau en mm) ; une transformation sera nécessaire.

Formulation de la méthode

Principes de la méthode

Pour appliquer la méthode, on s'appuie sur les courbes Intensité-durée-fréquence que l’on transforme en courbe hauteur-durée-fréquence (ou courbes enveloppes), soit, pour un ajustement de type Montana :

$ H(t,T)= a(T).t^{b(T)+1} \quad (1) $

Avec :

• $ H(t,T) $: Hauteur de pluie précipitée pour la durée $ t $ et la période de retour $ T $ ($ m $) ;
• $ a(T) $ et $ b(T) $ : Coefficients d’ajustement d’une formule de type Montana pour la période de retour $ T $ (à choisir pour obtenir $ H $ en $ m $ avec $ t $ en $ s $).

Dans la suite de l'article nous supposerons que les calculs sont faits pour une période de retour donnée $ T $ et nous noterons simplement ces grandeurs $ H(t) $, $ a $ et $ b $.

Le volume entrant dans l'ouvrage de stockage ($ V_p(t) $) pour une pluie de durée $ t $ se calcule donc simplement :

$ V_p(t) = C_a.S.H(t)= S_a.a.t^{b+1}\quad (2) $

Avec :

• $ C_a $ : coefficient d'apport ;
• $ S $ : surface totale du bassin versant drainé $ (m^2) $ ;
• $ S_a = C_a.S $ : surface active $ (m^2) $.

Comme le débit de vidange $ Q_v $ est supposé constant, le volume ($ V_r $) évacué après une durée $ t $ est simplement égal à :

$ V_r(t) = t.Q_v\quad (3) $

On peut alors calculer, pour chaque durée de pluie $ t $, la différence entre le volume entrant et le volume évacué, qui représente le volume à stocker $ V_S $ pour une pluie ayant cette durée $ t $ (Voir Figure 1) :

$ V_s(t) = V_p(t) – V_r(t)\quad (4) $

Soit :

$ V_s(t) = a.S_a.t^{(b+1)}-Q_v.t\quad (5) $

Figure 1 : Schéma de principe de la méthode des pluies ; Source : Chocat et Cherqui, 2018.

Il existe une durée $ t_m $ pour laquelle cette différence maximum. C'est donc pour cette durée qu'il faudra calculer le volume de stockage nécessaire pour la période de retour $ T $.:

Formulation analytique

La relation (5) permet de calculer le volume à stocker en fonction de la pluie. Ce volume sera maximum pour la durée $ t_m $ qui vérifiera :

$ \frac{dV_s(t)}{dt} = 0\quad (6) $

Soit :

$ a.(b+1).S_a.t_m^b-Q_v = 0\quad (7) $

D’où :

$ t_m^b = \left(\frac{Q_v}{a.(b+1).S_a}\right)\quad (8) $

et

$ t_m = \left(\frac{Q_v}{a.(b+1).S_a}\right)^{1/b}\quad (9) $

En reportant la relation (8) dans l’expression du volume stocké (5), il est possible de calculer le volume maximum $ V_{max} $ :

$ V_{max} = (a.S_a.t_m^b-Q_v).t_m\ $

$ V_{max} = \left(\frac{Q_v}{b+1}-Q_v\right).t_m\ $

soit :

$ V_{max} = \left(\frac{-b}{b+1}\right).Q_v.t_m\quad (10) $

Et finalement en reportant la relation (9) dans la relation (10), on obtient une formule permettant le calcul analytique direct de $ V_{max} $ en fonction de $ Q_v $ :

$ V_{max} = \left(\frac{-b}{b+1}\right).Q_v.\left(\frac{Q_v}{a.(b+1).S_a}\right)^{1/b} $

Il est alors possible de mettre en évidence une formule simple reliant directement $ V_{max} $ et $ Q_v $ (Chocat et Cherqui, 2018) :

$ \left(\frac{V_{max}}{C.Sa}\right)^b=\left(\frac{Q_v}{S_a}\right)^{b+1} \quad (11) $

Cette formule fait apparaître une constante C qui ne dépend que des coefficients de Montana :

$ C=\frac{-a.b}{\left(a.(b+1)\right)^{(b+1)/b}} \quad (12) $

Introduction de la durée maximum en eau

La figure 1 fait apparaître une autre durée intéressante : la durée $ t_{ee} $ qui correspond à la durée pour laquelle le débit de restitution moyen de l’ouvrage $ Q_v $ est égal au débit apporté à l’ouvrage. En d’autres termes, à partir de la durée $ t_{ee} $, l’ouvrage restitue de façon instantanée la totalité du volume apporté par la pluie et aucun stockage n'est nécessaire. La durée tee correspond donc à la durée maximum pendant lequel il peut y avoir de l'eau dans l'ouvrage. Cette durée est très importante pour des questions multiples : risque d'événements successifs, durée pendant lequel l'espace utilisé par l'ouvrage est inutilisable pour d'autres activités, risque d'éclosion de moustiques, etc.. Pour cette raison, il est généralement conseillé de limiter cette durée maximum en eau à quelques jours (typiquement 24 à 72h).

Nota : la pluie de durée $ t_{ee} $ n’est pas la même que la pluie dimensionnante de durée $ t_m $. La durée $ t_{ee} $ ne représente donc pas le temps de vidange de l’ouvrage plein, lequel sera forcément inférieur à $ t_{ee} $.

La durée $ t_{ee} $ est telle que les débits moyens entrant et sortant soient égaux, c'est à dire :

$ a.S_a.t_{ee}^b=Q_v \quad (13) $

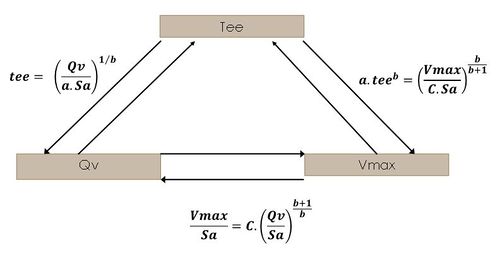
Il est donc possible d'écrire des relations explicites simples entre les 3 grandeurs $ t_{ee} $, $ V_{max} $ et $ Q_v $ :

$ a.t_{ee}^b=\frac{Q_v}{S_a}=\left(\frac{Vmax}{C.S_a}\right)^{b/(b+1)} \quad (14) $

Ces relations explicites sont schématisées sur la figure 2.

Figure 2 : Relations entre tee, Qv et Vmax ; Source : Chocat et Cherqui, 2018.

Choix des données pluviométriques

En l'absence de données locales disponibles dans beaucoup de collectivités, il est possible d'utiliser des ajustements de type Montana qui sont disponibles auprès de Météo-France pour chaque département et différentes périodes de retour. La principale précaution à prendre consiste à bien s’assurer que l’ajustement utilisé correspond bien aux durées pour lesquelles on réalise le calcul. En effet, les ajustements des courbes IDF ne sont valables que pour une plage donnée de durées (par exemple de 6 minutes à 2 heures) et peuvent conduire à des erreurs très importantes si on les utilise en dehors de cette plage de durée.

Moyennant cette précaution, la méthode des pluies donne des résultats satisfaisants si les trois hypothèses sur lesquelles elle repose sont remplies, ce qui est le cas pour la plupart des petits ouvrages de retenue (en particulier pour tous les ouvrages de stockage dits à la parcelle).

Bibliographie :

• Chocat, B. ; Cherqui, F. (2018) : La méthode des pluies revisitée ; TSM N°11 ; 2018 -; Page(s) 49-59.

Pour en savoir plus : Vidéo de présentation de la méthode des pluies généralisée

Voir aussi : Méthode des débits, Méthode des volumes.