A.08 - Probabilités

Quantifier l'incertitude : est-ce plus ou moins probable ?

Informer sur le degré d'incertitude peut passer par l'expression qualitative d'un indice de confiance (par exemple chez Météo-France, les prévisions sont qualifiées par un indice compris entre 1 et 5). Pour aller vers une information plus précise, il est possible de s'orienter vers une quantification de ce degré d'incertitude, ou encore du caractère plus ou moins vraisemblable que l'événement prévu ait lieu à travers la notion de probabilité.

Expressions mathématiques

Définition de la probabilité

Cette quantification du caractère plus ou moins probable d'un événement est faite mathématiquement en lui associant un nombre réel compris entre 0 et 1.

Le mot « événement » renvoie ici à n'importe quelle affirmation concernant un fait dont on n'est pas sûr :

• il pleuvra demain (oui / non) ;
• la valeur d'une grandeur inconnue (et considérée en conséquence aléatoire) comme la hauteur d'eau à la station dans 6 heures. L'événement est alors l'affirmation 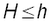où H est la variable aléatoire (inconnue) qu'est la hauteur d'eau dans 6 heures à la station et h une valeur (par exemple 1,43 m).

On note , a probabilité d'un événement. Ainsi, st la probabilité que la hauteur H de la rivière Senne à la station de Moulinsart soit supérieure au seuil HSeuil.

lus l'événement est considéré comme probable, plus ce nombre sera élevé. À un événement parfaitement certain, on associera la probabilité 1. Inversement à un événement impossible, on associera la probabilité 0.

Ce nombre compris entre 0 et 1 est souvent exprimé comme la proportion de « chance » de réalisation de l'événement. On dit ainsi communément qu'un événement de probabilité 0,5 a une chance sur deux de se réaliser.

La distribution de probabilité d'une variable aléatoire X caractérise les probabilités de tous les événements (pour la variable X). Elle peut être discrète si X ne prend qu'un nombre fini de valeurs (section 2.2) ou bien continue si la variable X peut prendre n'importe quelle valeur sur une partie continue des réels (section 2.3).

Cas d'une prévision discrète

Considérons un événement incertain qui ne peut prendre qu'un nombre fini de valeurs. Ce peut être par exemple de savoir si la hauteur d'eau dépassera ou non le seuil d'alerte (cet événement peut prendre deux valeurs : oui ou non), ou encore la couleur de vigilance à 16 h 00 (qui ne peut prendre que quatre valeurs : vert, jaune, orange et rouge).

Appelons X cette grandeur inconnue et x1, x2, …, xn les n valeurs qu'elle peut prendre. On associera alors à chaque valeur la probabilité p1, p2, … pn :

pour chaque valeur possible xi (i est compris entre 1 et n)

Si les valeurs discrètes peuvent être ordonnées1, on appelle probabilité de non dépassement ou fonction de répartition P, la probabilité des événements :

Exemple 1. Un dé (non pipé) lancé a 1 chance sur 6 d'aboutir à la valeur 4. La probabilité que le dé lancé donne la valeur 4 est donc de 1/6≈0.167. Considérons maintenant le jet de deux dés non pipés. La figure suivante présente à gauche la probabilité d'obtenir chaque valeur de tirage entre 2 et 12 (par exemple, il y a 4 manières sur 36 jets possibles d'obtenir un 5 : 1 + 4, 2 + 3, 3 + 2 et 4 + 1) puis la fonction de répartition (à droite).