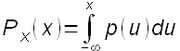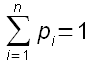A.08 - Probabilités
Sommaire |
Quantifier l'incertitude : est-ce plus ou moins probable ?
Informer sur le degré d'incertitude peut passer par l'expression qualitative d'un indice de confiance (par exemple chez Météo-France, les prévisions sont qualifiées par un indice compris entre 1 et 5). Pour aller vers une information plus précise, il est possible de s'orienter vers une quantification de ce degré d'incertitude, ou encore du caractère plus ou moins vraisemblable que l'événement prévu ait lieu à travers la notion de probabilité.
Expressions mathématiques
Définition de la probabilité
Cette quantification du caractère plus ou moins probable d'un événement est faite mathématiquement en lui associant un nombre réel compris entre 0 et 1.
Le mot « événement » renvoie ici à n'importe quelle affirmation concernant un fait dont on n'est pas sûr :
- il pleuvra demain (oui / non) ;
- la valeur d'une grandeur inconnue (et considérée en conséquence aléatoire) comme la hauteur d'eau à la station dans 6 heures. L'événement est alors l'affirmation H ≤ h où H est la variable aléatoire (inconnue) qu'est la hauteur d'eau dans 6 heures à la station et h une valeur (par exemple 1,43 m).
On note P(·), a probabilité d'un événement. Ainsi, P(H > HSeuil) est la probabilité que la hauteur H de la rivière Senne à la station de Moulinsart soit supérieure au seuil HSeuil.
Plus l'événement est considéré comme probable, plus ce nombre sera élevé. À un événement parfaitement certain, on associera la probabilité 1. Inversement à un événement impossible, on associera la probabilité 0.
Ce nombre compris entre 0 et 1 est souvent exprimé comme la proportion de « chance » de réalisation de l'événement. On dit ainsi communément qu'un événement de probabilité 0,5 a une chance sur deux de se réaliser.
La distribution de probabilité d'une variable aléatoire X caractérise les probabilités de tous les événements (pour la variable X). Elle peut être discrète si X ne prend qu'un nombre fini de valeurs (section 2.2) ou bien continue si la variable X peut prendre n'importe quelle valeur sur une partie continue des réels (section 2.3).
Cas d'une prévision discrète
Considérons un événement incertain qui ne peut prendre qu'un nombre fini de valeurs. Ce peut être par exemple de savoir si la hauteur d'eau dépassera ou non le seuil d'alerte (cet événement peut prendre deux valeurs : oui ou non), ou encore la couleur de vigilance à 16 h 00 (qui ne peut prendre que quatre valeurs : vert, jaune, orange et rouge).
Appelons X cette grandeur inconnue et x1, x2, …, xn les n valeurs qu'elle peut prendre. On associera alors à chaque valeur la probabilité p1, p2, … pn :
![]() pour chaque valeur possible xi (i est compris entre 1 et n)
pour chaque valeur possible xi (i est compris entre 1 et n)
Si les valeurs discrètes peuvent être ordonnées, on appelle probabilité de non dépassement ou fonction de répartition P, la probabilité des événements ![]() :
:
Exemple 1. Un dé (non pipé) lancé a 1 chance sur 6 d'aboutir à la valeur 4. La probabilité que le dé lancé donne la valeur 4 est donc de 1/6 ≈ 0.167. Considérons maintenant le jet de deux dés non pipés. La figure suivante présente à gauche la probabilité d'obtenir chaque valeur de tirage entre 2 et 12 (par exemple, il y a 4 manières sur 36 jets possibles d'obtenir un 5 : 1 + 4, 2 + 3, 3 + 2 et 4 + 1) puis la fonction de répartition (à droite).
Cas d'une prévision continue
On peut généraliser le cas précédent pour une grandeur qui peut prendre n'importe quelle valeur parmi les nombres réels. Ce sera par exemple la hauteur d'eau à venir au point de prévision.
Dans ce cas, la probabilité de l'événement X = x (la variable aléatoire X vaut exactement le réel x) est généralement infinitésimale. Par contre, on peut s'intéresser ici encore à la probabilité de non dépassement (qu'on appelle ici également fonction de répartition [1]) :
On définit alors la densité de probabilité p(x) pour toute valeur x réalisable :
On a donc pour toute valeur x réalisable [2] :
La probabilité que la valeur de la grandeur aléatoire soit comprise entre a et b est alors :
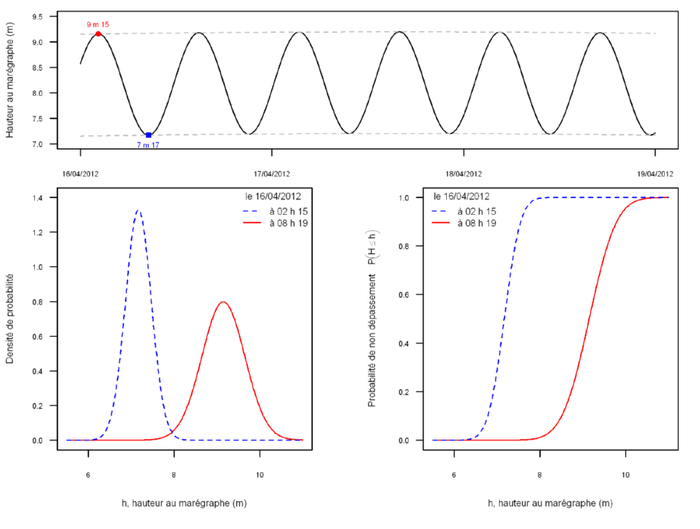
Exemple 2. La hauteur d'eau ou le débit qui sera observé dans 6 heures à la station de Saint-Nazaire peut prendre n'importe quelle valeur réelle positive. Le marégramme donne la prévision déterministe correspondant à des conditions de vent et de pression standard (figure ci-après, en haut). Cette prévision correspond à l'influence lunaire et solaire. Il reste donc une incertitude sur la hauteur d'eau à venir qui est représentée sur les graphes en bas avec à gauche, la densité de probabilité et à droite, la probabilité de non dépassement (fonction de répartition). Bien que la prochaine marée basse arrive plus tard que la prochaine marée haute, on peut constater que la prévision est moins incertaine (la distribution de probabilité est plus resserrée), ce qui peut être due ici à une prévision plus précise de la pression et du vent au moment de la marée basse.
Quelques propriétés fondamentales
La probabilité d'un événement prend des valeurs comprises entre 0 et 1. Par contre, une densité de probabilité, qui est une dérivée d'une probabilité, peut prendre des valeurs supérieures à 1, comme on peut le constater dans l'exemple 2. Il suffit pour cela que la distribution de probabilité soit suffisamment resserrée.
Dans le cas discret (section 2.2), la grandeur X ne peut prendre que l'une des n valeurs. On en déduit que la somme des probabilités p1, p2, … pn vaut 1 :
Par extension, dans le domaine continu (section 2.3), on a en sommant la probabilité de toutes les valeurs possibles :
Probabilités conditionnelles
La probabilité d'un événement A traduit notre connaissance (notre estimation) de sa vraisemblance. Sa probabilité n'est donc pas la même selon les informations dont on dispose.
Exemple 3. La probabilité que le dé donne un 5 est de 1 / 6 mais si on sait en plus que le résultat sera impair alors la probabilité passe à 1 / 3.
C'est pourquoi on distingue la probabilité de l'événement A, P(A), indépendamment de toute information extérieure, de la probabilité de l'événement A conditionnellement à une information supplémentaire B, P(A|B) qu'on lit souvent comme étant la probabilité de A sachant B. L'information B peut être de nature « déterministe » (un fait certain) ou bien bien prendre la forme d'une information probabiliste comme la (connaissance de la) densité de probabilité d'un événement aléatoire.
Exemple 4. ![]() est probabilité que le débit à venir à l'horizon H
est probabilité que le débit à venir à l'horizon H ![]() , soit inférieur à la valeur q. En l'absence de connaissance particulière sur le point de prévision, la densité de probabilité associée
, soit inférieur à la valeur q. En l'absence de connaissance particulière sur le point de prévision, la densité de probabilité associée ![]() sera vraisemblablement étalée (grande incertitude). Si nous disposons d'une prévision fournie par un modèle, nous nous tournerons vers la probabilité conditionnelle à cette prévision :
sera vraisemblablement étalée (grande incertitude). Si nous disposons d'une prévision fournie par un modèle, nous nous tournerons vers la probabilité conditionnelle à cette prévision :
-
 dans le cas d'un système de prévision déterministe fournissant la valeur
dans le cas d'un système de prévision déterministe fournissant la valeur 
-
 dans le cas d'un système de prévision probabiliste fournissant la densité de probabilité de
dans le cas d'un système de prévision probabiliste fournissant la densité de probabilité de 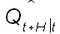
Approches mathématiques classiques
Par extension, on appelle « probabilités » les théories mathématiques qui posent les propriétés de ces objets et fournissent des méthodes pour les calculer. En particulier, vous avez pu lire ou entendre parler de probabilités fréquentistes ou bayésiennes. Celles-ci diffèrent par leurs postulats.
Approches fréquentistes
La probabilité est profondément associée à la fréquence de réalisation d'un événement. Poincaré définit (à la suite de Fermat et de Pascal) la probabilité d'un événement comme étant le rapport du nombre de cas favorables à cet événement au nombre total des possibilités.
Dans cette approche, on considère que la fonction de répartition existe de façon déterminée : ainsi, si la fonction est paramétrée, ses paramètres θ sont fixés (mais potentiellement inconnus). L'estimation de cette fonction de répartition (ou de ses paramètres θ) est incertaine car elle ne peut se baser que sur un nombre limité d'expériences ou de données. Elle serait certaine si on pouvait disposer d'une connaissance parfaite, c'est-à-dire si on disposait de toutes les données possibles (réalisation de toutes les expériences possibles). La probabilité s'interprète donc comme la limite atteinte par l'estimation de la fonction de répartition (ou de ses paramètres) à l'aide de n expériences ou données quand ce nombre d'expériences tend vers l'infini.
Exemple 5. En lançant un nombre infini de fois un dé non pipé, on déduit la probabilité d'obtenir le nombre 4 de la fréquence empirique d'apparition du nombre 4.
Approches bayésiennes
L'approche bayésienne réside sur le concept d'apprentissage lié à une expérience (ou à une donnée). La fonction de répartition (ou ses paramètres) ne sont pas des objets déterminés mais leur connaissance peut être affinée à l'aide d'expérience. Formellement, les paramètres de la fonction de répartition sont eux-mêmes des variables aléatoires. Le théorème de Bayes permet de calculer la connaissance sur la fonction de répartition après l'obtention d'une donnée (appelée posterior) à partir de la connaissance de la fonction de répartition avant l'expérience (prior) et de la vraisemblance de la donnée obtenue. La fiche C.06 décrit l'emploi de ces approches pour la prévision.
Voir également
Fiche C.06 – Approches bayésiennes
Pour aller plus loin
Boreux, J., Parent É., et Bernier J.-J. (2000). Statistique pour l'environnement, traitement bayésien de l'incertitude. Tec & Doc. ISBN : 9782743003555.
 S'abonner à un flux RSS
S'abonner à un flux RSS