B.26 - Modélisation hydraulique

Introduction

L'utilisation de modèles hydrauliques pour la prévision des crues a déjà été adoptée par de nombreux SPC sur les principaux fleuves français (la Seine et ses principaux affluents, la Loire, la Meuse ...). La mise à disposition de données (levés bathymétriques, relevés d'ouvrages, nivellements d'échelles, levés LIDAR) dans le cadre de la démarche mise en œuvre pour la prévision des inondations, la formation à la modélisation hydraulique et la mise à disposition de plate-forme de modélisation hydraulique (Mascaret, Télémac) créent des conditions favorables à une généralisation de la modélisation hydraulique sur les principaux cours d'eau.

Ainsi, la question de la qualité des résultats produits par ces modélisations doit être posée. Pour répondre à cette question, il est nécessaire de se pencher sur les différentes sources d'incertitude de la modélisation hydraulique :

• incertitudes liées aux données de construction des modèles : la topographie et la bathymétrie,
• incertitudes liées aux hypothèses de la modélisation,
• incertitudes sur le calage : coefficients de frottement, apports intermédiaires, paramètres hydrauliques,
• incertitudes liée à l'exploitation opérationnelle des modèles hydrauliques : les conditions initiales, les conditions limites amont et aval.

Nous allons passer en revue ces différentes sources d'incertitude et nous verrons, sur un exemple précis, les performances obtenues en calage et lors de l'exploitation en prévision de crue de ce modèle. Enfin, nous présenterons les possibilités d'amélioration des résultats des modèles hydrauliques en corrigeant certaines sources d'incertitudes avec des techniques d'assimilation de données.

Construction des modèles hydrauliques

La construction d'un modèle hydraulique nécessite de disposer de données topographiques décrivant le lit de la rivière et ses éventuels bras secondaires (lit mineur), la plaine inondable (lit majeur) et tous les ouvrages influant sur les écoulements (digues de protection contre les crues, barrages de navigation, ponts...).

Les relevés du lit mineur sont réalisés par des relevés terrestres (nivellement classique ou relevés GPS) et, pour la partie sous l'eau, par sondage. La précision des mesures dépend des contraintes imposées au géomètre par le cahier des charges : densité des points, précision de la mesure altimétrique et planimétrique. En général, la précision altimétrique demandée est meilleure que 0,10 m, la densité de points de l'ordre d'un point tous les 2 à 10 mètres, la précision planimétrique de l'ordre du mètre. Le rattachement au NGF est fait par levé terrestre ou par GPS. Sa précision est de l'ordre de quelques centimètres voire mieux. Les relevés bathymétriques étant onéreux, leur nombre est forcément limité et doit être adapté à la taille du cours d'eau (un profil tous les 5 à 10 fois la largeur du lit) et leur localisation choisie pour représenter les points singuliers du cours d'eau : franchissements, présence de seuils, élargissement ou rétrécissement du lit...

La description du lit majeur se faisait traditionnellement par des levés de profils en travers, souvent dans le prolongement du relevé du lit mineur. Dans ce cas, compte tenu de la longueur parfois importante de ces profils (plusieurs kilomètres dans le cas de la Loire), la densité de points demandés au géomètre est réduite, de l'ordre d'un point tous les 20 à 50 mètres. La précision de ce levé, par levé terrestre ou par GPS, est de l'ordre de quelques centimètres. Depuis quelques années, la technique du levé par laser aéroporté (LIDAR) s'est imposée dès lors que les surfaces à couvrir étaient d'importance. L'ensemble des SPC doivent disposer, dans les toutes prochaines années, de relevés de ce type sur la plupart de leurs cours d'eau. Le LIDAR permet d'obtenir une densité de point considérable, de l'ordre d'un point par mètre carré. Cette densité permet de représenter finement la micro-topographie de la vallée. On distingue ainsi les chenaux de crue éventuels, les routes en remblai, les terrasses alluviales... La précision de ces relevés est meilleure que le mètre en planimétrie et de l'ordre de 10 à 20 cm en altimétrie. Compte tenu du poids de ces données, leur utilisation directe pour la modélisation hydraulique n'est en général pas possible (cf plus loin sur les hypothèses de la modélisation hydraulique). Il est alors nécessaire d'extraire de ces levés LIDAR des profils en travers décrivant le lit majeur.

La description des digues peut se faire soit par un relevé du profil en long de la crête de digue, soit en récupérant ce profil à partir du levé LIDAR, soit en se limitant aux cotes relevés lors du levé du profil en travers de la vallée. Dans ce dernier cas, il faut s'assurer que l’on ne passe pas à côté de points singuliers comme une interruption de la digue, un point bas, un ouvrage de décharge.

La description des ouvrages (barrages, seuils de prise d'eau, ponts) peut être récupérée auprès des gestionnaires d'ouvrage. Parfois, il est nécessaire ou préférable de recourir à un géomètre pour refaire le relevé de ces ouvrages (ouvrages modifiés, absence de rattachement au NGF, relevé incomplet...). la précision de ces plans existant ou relevés est en général de l'ordre du centimètre.

À l'incertitude des techniques de levés topographiques et bathymétriques, il faut rajouter l'incertitude liée aux évolutions dans le temps des lits mineurs (notamment dues au transport solide) et majeurs qui peuvent localement induire une incertitude non négligeable sur la connaissance des conditions d'écoulement.

Hypothèses de la modélisation

La modélisation hydraulique 1D repose sur la résolution des équations de Barré – Saint-Venant. Celle-ci est fondée sur une série d'hypothèses dont les principales sont :

• l'écoulement est unidimensionnel (ou filaire) ;
• la répartition des vitesses est uniforme dans une section transversale donnée ;
• la répartition des pressions sur une verticale est hydrostatique.

À l'échelle d'une vallée et pour l'objectif qui est le nôtre (à savoir la propagation des crues pour la prévision aux échelles de crue), ces hypothèses peuvent être considérées comme étant satisfaites. Le modèle pourra toutefois mal représenter les écoulements dans des zones de confluence et à proximité de points singuliers. Les échelles de prévision étant souvent situées sur des ouvrages constituant des points singuliers, le modèle pourra ainsi avoir des difficultés à reproduire l'ensemble des cotes à ces échelles.

Au-delà de ces hypothèses, la construction du modèle nécessite également de définir une topologie c'est à dire une schématisation du fonctionnement hydraulique du cours d'eau et de sa vallée. Ainsi, par exemple, il faut définir :

• les zones d'écoulement (décrites par des modélisations filaires) et les zones de stockage (décrites par des casiers),
• les points d'échange entre ces zones (communication au niveau du terrain naturel, débordement par-dessus une digue...),
• la représentation des différents écoulements par les modèles filaires : le bras principal, les bras secondaires éventuels, les chenaux de crues en lit majeur.

La modélisation hydraulique 1D reste ainsi une schématisation du fonctionnement hydraulique réel du cours d'eau.

Prise en compte des apports intermédiaires

La prise en compte des apports intermédiaires est délicate : tous les cours d'eau n'étant pas instrumentés, on ne dispose pas d'hydrogrammes d'entrée pour chaque affluent. Pour un modèle situé en tête de bassin il est indispensable de tenir compte des apports intermédiaires au risque de largement sous-estimer les débits et par conséquent les hauteurs d'eau modélisées. Dans ce cas plusieurs solutions s'offrent au modélisateur :

• injecter entre chaque station d'observation un débit moyen constant représentatif du déficit moyen de débit constaté à la station à l'aval. Cela peut fonctionner lorsque la variabilité hydrologique est faible. C'est par exemple le cas pour les cours d'eau crayeux du modèle Mascaret Marne Moyenne du SPC SAMA ;
• injecter un hydrogramme voisin multiplié par un coefficient multiplicateur. Ce dernier peut être déterminé en fonction de la surface du bassin versant de l'apport que l'on souhaite injecter dans le modèle ou peut être calé (on déterminera alors un coefficient moyen pour les différentes crues de calage). Cette solution implique une répartition homogène des pluies et que les comportements hydrologiques des cours d'eau soient comparables. Cette solution est utilisée pour le modèle Mascaret Marne Amont Global au SPC SaMa ;
• caler des modèles pluie-débit pour modéliser les principaux apports. Cette solution peut se révéler plus fiable. Elle est coûteuse en termes de temps (pour le calage). De plus, cela implique d'enchaîner les modélisations hydrologiques et hydrauliques.

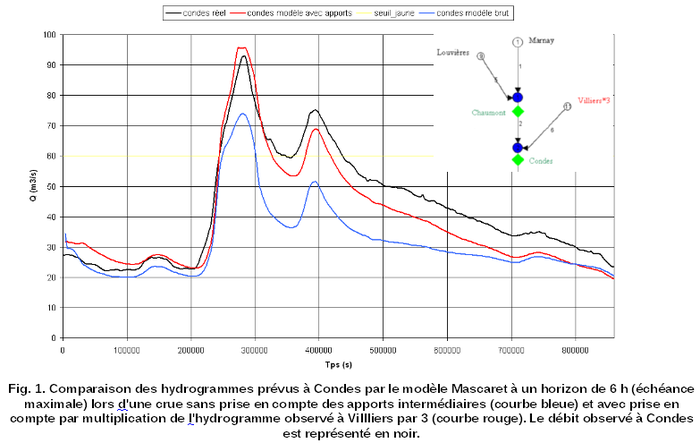
Exemple 1. Le SPC SaMa emploie le modèle hydraulique Mascaret pour sa prévision à Condes (en tête du bassin de la Marne). Les performances du modèle dépendent de la prise en compte des apports intermédiaires. Elles ont été comparées sans prise en compte et avec une prise en compte basée sur la multiplication de l'hydrogramme de la station de Villiers par un facteur constant (3). La prise en compte améliore nettement la modélisation des débits (Fig. 1).

La prise en compte des apports intermédiaires est une source d'incertitude, tant lors du calage du modèle hydraulique, qu'en conditions opérationnelles dont il faut tenir compte en plus de l'incertitude bien connue sur les observations de hauteur (et les estimations de débit).

Calage des modèles hydrauliques

Nous nous restreignons ici au calage des modèles hydrauliques de type 1D [1], avec ou sans casier (comme Mascaret, Hydra, Mike 11). Le calage de ces modèles consiste en pratique à établir la valeur de la rugosité des lits mineurs et majeurs (coefficients de Strickler) et des échanges entre les différents lits (bras) et entre le lit et les casiers d'inondation, ainsi que les paramètres liés aux ouvrages singuliers : loi de seuil pour des vannages ou des déversoirs, loi de perte de charge pour les ponts et autres ouvrages de franchissement.

La réalisation de ce calage nécessite de disposer de données d'observation faites durant une ou plusieurs crues, dans l'idéal couvrant des crues pas ou faiblement débordantes (calage du lit mineur) et fortement débordantes (calage du lit majeur). Ces données peuvent être :

• des hydrogrammes aux entrées du modèle,
• des relevés de ligne d'eau faites au passage de la crue, si possible lors de son maximum,
• des relevés de laisse de la crue ou des relevés de repères de crues,
• des prises de vues aériennes,
• des enregistrements limnigraphiques ou des relevés d'échelles,
• des courbes de targe au droit des échelles hydrométriques.

La disponibilité et la densité de ces données est très variable. Le rassemblement et la critique de ces données représente un travail important mais primordial pour la qualité du calage du modèle. La mise en place d'une véritable stratégie d'acquisition des données (création de réseaux d'observation, disponibilité de marchés pour faire intervenir des géomètres ou réaliser des prises de vue, mise en place d'une organisation pour la réalisation de jaugeages de crues) permet d'améliorer la connaissance des écoulements en crue et par-delà, d'améliorer le calage du modèle et d'assurer sa mise à jour.

Si on ne dispose que des relevés aux échelles, en l'absence de mesures intermédiaires le long du cours d'eau, le calage du modèle ne pourra être que global (les valeurs des différents coefficients seront homogènes et/ou issues de la littérature). On s'attachera à reproduire au mieux les observations disponibles à ces échelles. La représentativité par le modèle des écoulements le long du cours d'eau sera approximative : la précision altimétrique de la ligne d'eau est alors généralement de l'ordre du mètre.

Dans le cas ou l'on dispose d'observations denses et précises de la ligne d'eau, le calage du modèle peut être affiné localement. Il peut permettre de reproduire ces lignes d'eau avec une précision de l'ordre de 20 à 30 centimètres, voire mieux dans les cas les plus favorables.

La représentation au droit des points singuliers est souvent faite à partir de formules théoriques (loi de perte de charge de type Bradley pour les ponts, loi de déversoir, etc.). Des observations peuvent permettre de vérifier, voire de préciser les valeurs calculées par le modèle.

Incertitudes liée à l'exploitation opérationnelle des modèles hydrauliques

En temps réel, les débits d'entrée du modèle sont entachés d'erreurs ainsi que pour les modèles maritimes la condition limite aval, le marégraphe. Pour ces sources d'incertitude, on peut se référer aux fiches 2.08 à 2.12 et à la fiche 2.28.

Les modèles hydrauliques sont généralement employés de façon événementielle, ce qui peut induire des incertitudes liées à leur initialisation. Par exemple, le modèle hydraulique Mascaret ne recalcule pas sa condition initiale (hauteurs et débits de base) à chaque simulation (celle-ci est fixée en dur dans un fichier). Or, en conditions opérationnelles, le temps ne permet pas le recalcul de la ligne d'eau initiale en fonction des hauteurs et des débits observés au moment de la simulation. Si la ligne d'eau initiale n'est pas adaptée, le modèle va mettre un temps équivalent au temps de propagation entre la station d'entrée la plus en amont et la station de sortie la plus en aval pour simuler des hauteurs et des débits situés dans la gamme de ceux observés aux stations. Pour contourner ce problème, il est conseillé de débuter la simulation plusieurs jours avant la date en cours afin de stabiliser l'erreur engendrée par la condition initiale (temps de chauffe ou warm-up, voir la fiche 2.24), ce qui implique d'avoir des données pour les quelques jours antérieurs. De plus, il est possible de créer plusieurs lignes d'eau initiale pour simuler les basses, moyennes ou hautes-eaux.

Performance des modèles hydrauliques en calage et en contrôle

Comme nous l'avons vu précédemment, la performance d'un modèle hydraulique dépendra de la qualité et de la richesse des données de construction et de calage disponibles. Il est nécessaire d'estimer ces performances à la fois au calage et en conditions pseudo-opérationnelles pour quantifier l'incertitude des prévisions. Cette quantification doit ensuite être analysée à l'aune des incertitudes sur les données observées (débits, hauteurs) auxquelles on a comparé les résultats du modèle au cours du calage.

Exemple 2. L'exemple qui suit porte sur le modèle hydraulique réalisé sur la Loire moyenne, initialement pour des études de stratégie de réduction du risque d'inondation et adapté en 2009 pour la prévision des crues. Lors de cette adaptation, le modèle initial a été complété, actualisé et son calage a été refait en utilisant notamment des observations faites durant la forte crue de décembre 2003. De nombreux tests ont été réalisés sur le modèle à l'issue de ce recalage. Ils permettent de donner une indication sur la précision du modèle. Compte tenu de nos objectifs, nous nous attacherons principalement à deux critères :

• écart entre la valeur du débit maximum calculé et observé,
• écart entre l'heure du passage du maximum calculée et observée.

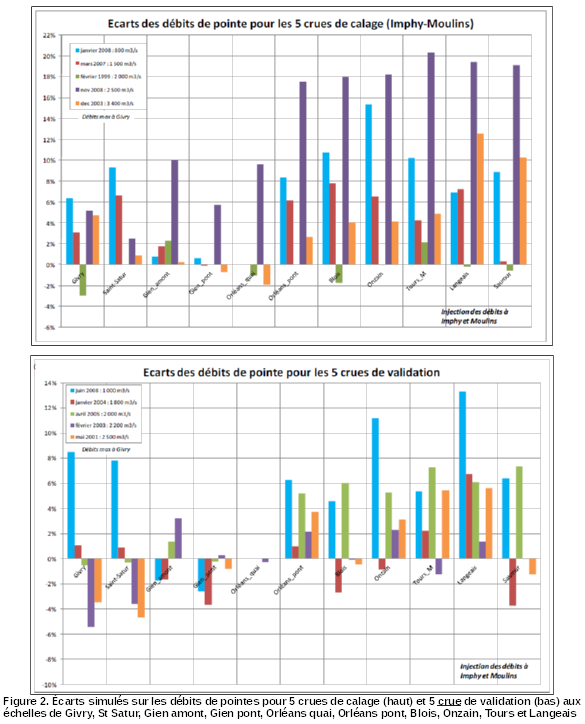
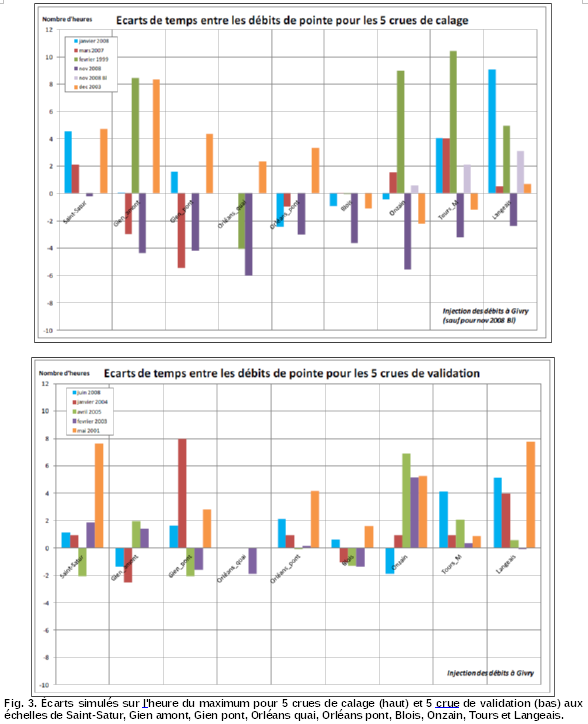
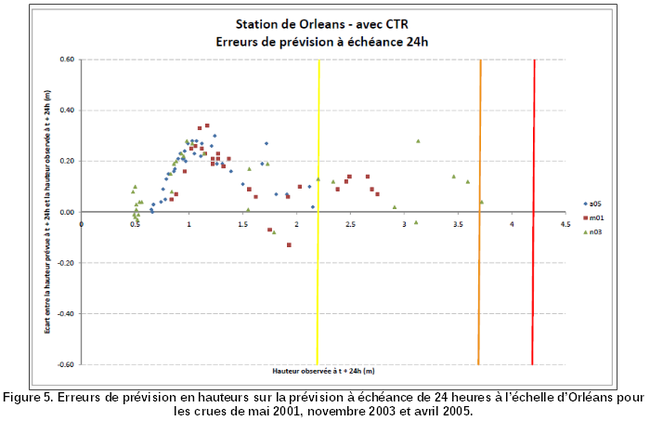
Des tests de performance ont été réalisés pour 5 crues de calage et 5 crues de validation (Fig. 2). Ces écarts ont également été établis en cote aux échelles (Fig. 3).

Les écarts sur les débits de pointe simulés aux échelle sont en général inférieurs à 10 % (la majorité des écarts se situent entre – 5 et + 5 %). Certaines crues restent toutefois mal reproduites par le modèle avec des écart qui dépassent largement 10 %. Les débits simulés sont en général surestimés à l'aval d'Orléans.

Les écarts sur l'heure du maximum ne dépassent pas 10 heures et sont, en général, inférieurs à 5 heures. Il n'y a pas de dégradation des performances du modèle sur ce critère en allant vers l'aval.

Performance des modèles hydrauliques en mode prévision

Les performances du modèle en calage ne sont pas celles qui seront obtenues en prévision lors de son utilisation en opérationnel. Une incertitude supplémentaire sera ajoutée du fait de l'incertitude sur les hydrogrammes amont aux point d'infection du modèle. Par contre, une procédure de traitement des erreurs de prévision est souvent mise en œuvre. Des tests de performance en situation pseudo opérationnelle ont ainsi été menés en phase finale de l'étude.

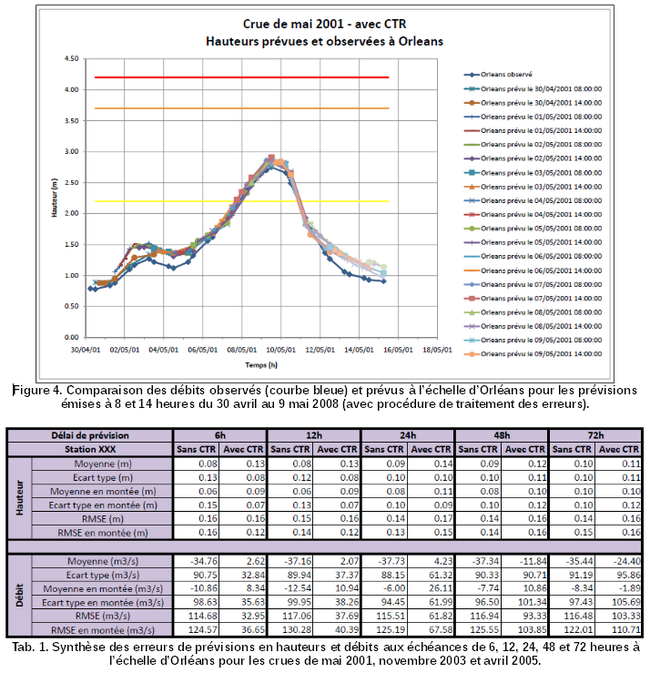
Exemple 2 (suite). Le modèle hydraulique a été découpé en plusieurs sous-modèle successifs afin de permettre d'introduire une procédure de recalage de la prévision aux stations intermédiaires. Des tests de performance ont alors été réalisés en situation pseudo-opérationnelle pour 3 crues et ont permis d'évaluer la qualité des prévisions émises pour des prévisions émises 2 fois par jours pour des échéances de 6 , 12, 24 , 48 et 72 heures.

Ces tests de performance peuvent être présentés sous différentes formes graphiques (Fig. 4 et 5) ou par des tableaux de synthèse (Tab. 1). Ils donnent une bonne idée des erreurs commises par le modèle en situation pseudo-opérationnelle. Ils renseignent également sur les biais éventuels du modèle (par exemple, le modèle parait surestimer les cotes entre 0,60 m et 1,50 m). Ils nous fournissent ainsi une bonne indication sur l'incertitude des résultats du modèle de prévision.

Prise en compte des incertitudes pour améliorer la modélisation : l'assimilation de données

La topographie, la bathymétrie, les coefficients de frottement, les débits d'entrée et d'apports intermédiaires, et les conditions initiales sont sources d'incertitude : elles engendrent des écarts entre les données modélisées (appelé ébauche) et observées. Il est possible de réduire ces écarts en modifiant certains paramètres ou certains états du modèle en fonction des observations les plus fraîches et de notre connaissance des différentes sources d'incertitude. Ce processus est appelé assimilation de données.

Exemple 3. Des procédures d'assimilations ont été testées et validées pour différents modèles Mascaret utilisés au sein du réseau de la prévision des crues.

Opérationnellement, les hauteurs ou les débits aux stations d'observations sont assimilés et comparées à l'ébauche. Des perturbations sont générées sur les débits d'entrée du modèle et/ou les coefficients de frottement. La réponse à cette perturbation est analysée et une modification « optimale » de ces états ou paramètres est choisie en fonction :

• de l'écart entre l'ébauche et l'observation,
• de notre connaissance quantitative des différentes incertitudes liées à l'observation (écarts-types d'erreur d'observation)
• de notre connaissance quantitative de l'incertitude de modélisation (écarts-type d'erreur sur les paramètres estimés au calage, comme le coefficient multiplicateur pour les apports intermédiaires ou les coefficients de rugosité).

Cette modification est « optimale » dans le sens où elle correspond à un équilibre entre les différentes sources d'incertitude à prendre en compte.

Cette procédure d'assimilation de données peut être répétée en temps réel (cycles) afin d'optimiser les paramètres sources d'erreurs et de réduire les écarts entre les données modélisées et observées.

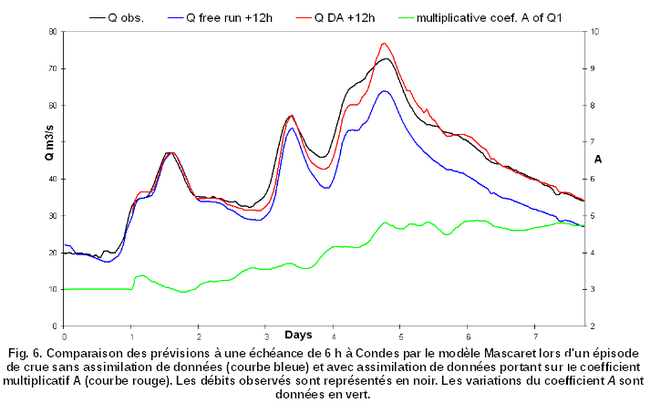
Exemple 1 (suite). Le coefficient multiplicateur A appliqué à l'hydrogramme de Villiers (3 à l'origine) pour prendre en compte les apports intermédiaires est modifié dans le temps (au cours d'un épisode de crue) pour réduire l'écart entre les débits prévus et observés à Condes (Fig. 6).

Conclusions

La construction d'un modèle hydraulique nécessite l'emploi de nombreuses données topographiques. Ces données sont entachées d'incertitudes. La construction du modèle nécessite également de faire des choix de représentation du cours d'eau et de sa vallée qui sont une schématisation simplifiée de la réalité, qui est une autre source d'incertitude. La qualité du calage du modèle enfin dépendra beaucoup de la disponibilité de données d'observations en crue.

La réalisation de test de performance du modèle final sur des crues de validation donne une première indication sur la capacité du modèle à reproduire la propagation des crues. Des tests supplémentaires en situation pseudo opérationnelle permettent d'aller plus loin. Ils nous apportent des éléments précis sur les performances réelles du modèle (en mode prévision) intégrant les procédures de traitement d'erreur qui seront mises en œuvre comme l'assimilation de données.

[1] Les modèles 2D sont rarement utilisés pour la prévision des crues. Un exemple notable est le modèle sur l'estuaire de la Gironde.

---

Voir également

• Fiche 2.08 – Mesure de la hauteur d’eau
• Fiche 2.09 – Incertitudes de la courbe de tarage
• Fiche 2.10 – Détarage en cours d’événement : incertitudes induite selon les types de cours d’eau
• Fiche 2.11 – Incertitudes de la mesure du couple (hauteur – débit) lors du jaugeage
• Fiche 2.12 – Quantification des incertitudes liées aux hauteurs d'eau et aux débits mesurés
• Fiche 2.24 – Initialisation des modèles hydrologiques et incertitude résultante
• Fiche 2.27 – Influence maritime en façade et en estuaire (marée et surcote)