ANSWER - Evolution des chenaux de navigation soumis au transport solide
Sommaire |
Éléments de contexte
Cette fiche a été conçue dans le cadre du projet de sciences participatives ANSWER. Elle contient le développement d'un modèle mathématique morphodynamique ainsi qu'une vidéo représentant une expérimentation réalisée sur la plage des Rochelets à Saint-Brévin visant à illustrer le phénomène d'évolution des chenaux de navigation soumis à des courants de marée.
Le modèle mathématique a été calé sur la base d'essais en laboratoire réalisés par Fredsoe (1968).
Déformation latérale des chenaux à fond mobile
Les effets du transport solide sur les fleuves et les littoraux
Le processus de transport solide concerne aussi bien les cours d'eau et les rivières que le littoral. Dans les bassins versants amont, l'eau de pluie ravine en surface et entraine les particules de sol qui vont rejoindre les parties amont de cours d'eau. Les volumes d'eau et de sédiments transportés sont parfois très importants et génèrent des débits élevés, qui s'accompagnent d'érosion et de transport de blocs de pierre de grandes dimensions. Vers l'aval, la pente des cours d'eau diminue, le gabarit s'élargit, la taille des sédiments décroit. Arrivés en plaine, les sédiments deviennent des sables et leur transport va dépendre des caractéristiques morphodynamiques de la rivière. Ce courant très chargé en sédiment, va lui même influencer ce milieu, érodant des zones à fort courant et déposant des sédiments dans des zones plus tranquilles. En mer, c'est exactement le même processus, mais le transport des sédiments dépend des courants océaniques, littoraux et du régime des houles.
Nous nous intéresserons ici aux chenaux de navigation, dont le tracé et la profondeur sont maintenus par des campagnes de dragages récurrentes, qui ont pour objectif d'évacuer les sédiments (vases ou sables) déposés par les courants, que ce soit en mer ou en rivière, permettant ainsi un accès tout au long de l'année aux bateaux fréquentant les ports maritimes ou fluviaux.
Nous simplifierons notre objet d'étude en considérant que le courant à l'intérieur du chenal est colinéaire à l'axe du chenal, ce qui n'est pas toujours le cas lors de crues de cours d'eau ou en mer où la direction du courant de marée fluctue en intensité et en direction.
Dans la suite de cette présentation, nous allons nous intéresser à la transformation géométrique de chenaux à fonds mobiles soumis à l'action d'un courant.
Pour cela, nous allons considérer un chenal rectiligne, de gabarit constant, dont le fond est constitué de sable et soumis sur l'ensemble de sa section au transport solide. Dans le cas de pentes relativement douces, nous négligerons les courants transversaux en considérant que les filets liquides dans l'ensemble de la section sont parallèles à l'axe du canal.
Dans certaines conditions, le transport de sédiment peut s'exercer partiellement ou en totalité :
- en suspension dans la masse du fluide : les particules suivent alors la vitesse du courant;
- par charriage, en restant en contact avec le fond : les particules sont alors soumises à la gravité et le transport des particules n'est plus colinéaire à la vitesse du fluide.
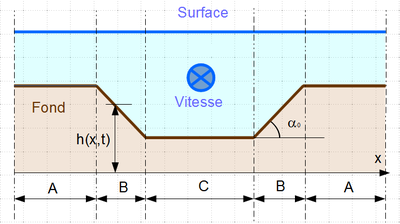
C'est ce dernier cas que nous allons plus particulièrement étudier. Le schéma ci-dessous représente le domaine pris en compte.
Nous allons tenter de reproduire la transformation dans le temps du profil transversal de ce chenal par une approche mathématique simplifiée, complétée par des essais sur modèle physiques réalisés par Fredsoe en 1978.
Expérimentation en nature
Afin d'illustrer les effets d'un courant de marée sur la déformation des chenaux de navigation, nous avons conduit une expérimentation sur la plage des Rochelets à Saint-Brévin (44) (Figure 2).
Figure 2: Localisation du site d'expérimentation à Saint-Brévin (44)
La vidéo ci-dessous illustre l'opération (Figure 3). Nous avons construit en arrière plage un petit chenal d'environ 4 m de long sur 1 m de large orienté dans le sens du flux/reflux de la marée. Ce chenal a été obstrué aux 2 extrémités dans un premier temps pour éviter que l'eau n'envahisse progressivement le modèle: nous souhaitions observer le processus de transport dans sa phase de démarrage.
Nous sommes partis d'un gabarit trapézoïdal et avons dans un premier temps ouvert le chenal aux 2 extrémités lorsque le niveau d'eau était assez élevé. Le courant résultant fut assez violent et le fond s'est tapissé assez rapidement de rides.
Nous avons ensuite laissé évoluer le chenal pendant 24 heures, soit 2 cycles de marée.
En revenant sur le site le lendemain, nous avons observé que le chenal avait subit de fortes évolutions : il était en effet recouvert entièrement de rides, le gabarit s'était ouvert et le fond avait sédimenté.
Ce cas illustre de manière très qualitative le processus de transformation des chenaux de navigation soumis au transport de matériaux, qui a été étudié en laboratoire (voir ci-dessous) et reproduit par un modèle mathématique que nous décrivons ci-dessous.
Plage des Rochelets Saint-Brévin - Expé chenal... par Wikhydro
Figure 3 : Expérimentation sur la plage des Rochelets à Saint-Brévin (44)
Expérimentation en canal et modélisation (Fredsoe, 1978)
Fredsoe (1978) étudia ce phénomène de transformation des profils des chenaux de navigation à fond mobile en laboratoire en réalisant 2 expériences sur un canal de 2 m de large et de 25 m de long, horizontal à débit liquide constant. La première expérience (run A) comportait un lit de sable de 18 cm d'épaisseur à l'intérieur duquel était creusé un chenal symétrique trapézoïdal de 8,5 cm de profondeur, de 40 cm de largeur de fond (C) et de 120 cm de plafond (2B+C). Le diamètre moyen du sable était de 1,18 mm. [run A = (18, 8,5, 40, 80, 1,18)]. Sa seconde expérience avait les propriétés suivantes : [run B = (15, 6, 40, 80, 0,55)]. Dans les 2 cas, le débit liquide était maintenu constant avec une profondeur d'eau de 50 cm. Les premiers 3 m du chenal étaient recouverts de petits cailloux de diamètre 2 cm pour casser les courants secondaires. La longueur de la partie mobile était de 7,5 m. Les mesures ont été faites selon un profil en travers situé 4 m à l'aval du début de la section mobile.
Compte tenu de ces paramètres, l'ensemble du transport se passe par charriage et aucune suspension n'est apparue. La valeur initiale de la vitesse du courant était respectivement de 0.60 m/s pour le run A et de 0.51 m/s pour le run B; la profondeur d'eau de 0,25 m pour le run A et de 0.1 m pour le run B.
Le fond s'est vite tapissé de dunes, ce qui a modifié les conditions locales d'écoulement, notamment la vitesse moyenne et la profondeur d'eau, sachant que le débit était maintenu constant. L'angle au repos du sable était de 32 degrés et l'angle de friction dynamique de 27 degrés.
Expérimentation au laboratoire d'IRSTEA à Lyon
Dans le but d'étudier ces processus d'évolution transversaux des chenaux de navigation, nous avons reproduit ces essais dans un canal à fonds mobiles du laboratoire d'hydraulique d'IRSTEA à Lyon.
En voici une présentation générale :
IRSTEA évolution chenaux de navigation par Wikhydro
Figure 4 : Expérimentation en canal de laboratoire d'IRSTEA à Lyon
Ces essais seront prochainement exploités et les données rendues disponibles sur WIKHYDRO
Explication qualitative du processus
Nous allons nous intéresser à ce qui se passe au droit d'un profil en travers.
Le gabarit est trapézoïdal (Figure 1), ce qui détermine 3 zones distinctes :
(i) la partie supérieure du lit (A) – de part et d'autre du chenal - initialement horizontale, (ii) les pentes du trapèze (B) et (iii) le fond (C)
Dans les paries horizontales (A et C), les particules se déplacent longitudinalement dans l'axe du chenal avec les dunes, ce qui maintient ces zones à l'horizontal. Par contre, sur les versants du chenal, les particules sont affectées par la gravité et durant leur transport, descendent vers le fond.
On assiste donc sur l'ensemble de la section étudiée, à une évolution du gabarit du chenal qui s'érode dans la partie supérieure du trapèze et qui sédimente dans la partie inférieure.
Un régime uniforme s'instaure donc tout au long du bief (7,5 m) étudié par les auteurs où est observée la transformation transversale du gabarit, toutes choses étant égales par ailleurs.
Nous limiterons donc notre étude à l'évolution transversale du profil en travers moyen du chenal.
Modélisation mathématique
Nous nous intéresserons donc ici uniquement à ce qui se passe dans la section du chenal en reprenant la démarche et les formules empiriques utilisées par Fredsoe.
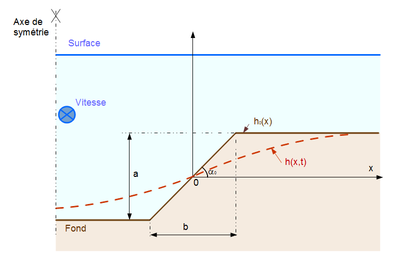
Soit $ \vec{V_f} $ la vitesse du fluide, colinéaire à l'axe du chenal, $ h $ le niveau du fond par rapport à un plan de référence, $ \alpha $ l'angle de la pente du fond ($ \alpha_0 $ étant l'angle à $ t=0 $ (Figure 4). Comme nous l'avons indiqué, les particules du fond qui sont transportées par le courant sont déviées par l'effet de la gravité, d'un angle $ \psi $..
Engelund (1972) propose la formule empirique suivante qui relie l'angle de friction dynamique $ \Phi $ et $ \psi $ :
$ (1)\qquad \tan{\psi}=\frac{\tan\alpha}{\tan\Phi}=-\frac{1}{\tan\Phi}\frac{\partial h}{\partial x} $
En effet $ \tan\alpha=-\frac{\partial h}{\partial x} $
Ainsi les vecteurs transport de sédiment sont reliés par l'expression suivante:
$ (2)\qquad \vec{q_{bt}}=\tan{\psi}\,\vec{q_{b}} $
dans laquelle $ \vec{q_{b}} $ est le transport dans l'axe de l'écoulement et $ \vec{q_{bt}} $ la composante transversale. C'est cette composante transversale qui est à l'origine du transport dans le profil. Elle peut donc s'exprimer par une équation de conservation de la manière suivante :
$ (3)\qquad\frac{\partial {q_{bt}}}{\partial x}= -(1-n)\frac{\partial h}{\partial t} $
$ n $ est la porosité du matériaux constituant le fond $ (n\backsim 0.45) $. Combinant (1), (2) et (3), nous obtenons;
$ (4)\qquad\frac{\partial h}{\partial t}=\frac{1}{(1-n)\tan\Phi} \dfrac{\partial {} }{\partial x} \left( q_b \dfrac{\partial h}{\partial x}\right) $
La valeur du débit solide $ q_b $ varie avec la profondeur et donc avec l'abscisse. Dans une première hypothèse, l'auteur considère que les variations de la profondeur d'eau sont faibles dans la direction transversale, ce qui permet de considérer la débit solide comme uniforme dans toute la section. Ainsi:
$ (5a)\qquad \frac{\partial h}{\partial t}=\nu \frac{\partial^2 h}{\partial x^2}<br /> $
avec
$ (5b)\qquad \nu=\frac{q_b}{(1-n)\tan\Phi} $
Conditions initiales et conditions limites
L'auteur fait une seconde hypothèse qui consiste à localiser la zone de transition entre érosion et dépôt au milieu du versant, ce qui est bien confirmé par l'expérience. Il positionne ainsi l'origine du système de coordonnées $ (h,x) $ en ce point (Figure 5).
Figure 5 : Déformation du profil en travers du chenal
Nous limiterons les développements mathématiques à un seul versant qui sera considéré comme infini dans les deux directions ($ x $ et $ -x $).
Pour obtenir l'évolution finale d'un profil trapézoidal qui comprend 2 versants, nous sommerons les évolutions des fonds provenant des 2 versants.
L'équation (5) est donc utilisée pour simuler la déformation dans le temps du profil transversal du chenal, associé aux conditions initiales et limites suivantes :
Conditions Initiales
- (6a) $ \qquad h_0(x)=h(x,t=0)=\tan\alpha_0x=\frac{a}{b}x, \; \forall x\in [-b/2,+b/2] $
- (6b) $ \qquad h_0(x)=h(x,t=0)=-a/2, \; \forall x\in ]-\infty,-b/2] $
- (6c) $ \qquad h_0(x)=h(x,t=0)=+a/2, \; \forall x\in [b/2,+\infty[ $
Conditions limites
$ (6d)\qquad h(x\rightarrow+\infty,t)=a/2 $ $ (6e)\qquad h(x\rightarrow-\infty,t)=-a/2 $
(6b) et (6e) supposent que l'on néglige les effets de bord du chenal.
Résolution du système d'équations
Pour résoudre ce système d'équations constitué des équations et relations (5) et (6), nous allons utiliser l'analyse du signal.
Pour cela, nous avons un signal de départ qui est constitué du profil trapézoïdal du chenal à l'instant initial : $ h_0(x)=h(x,t=0) $.
Ce signal est soumis à une fonction de transfert $ \mathcal{T}(x,t) $ représentée par l'équation linéaire (5) qui va faire évoluer ce signal initial au cours du temps. Le signal de sortie sera donc la convolution de ces 2 fonctions:
$ (7)\qquad h=h_0(x)*\mathcal{T}(x,t) $
Pour simplifier les notations, nous poserons $ \nu=1 $, ce qui permet d'écrire (5) sous la forme concise: $ h_{t}=h_{xx} $.
Pour résoudre l' équation linéaire (5), nous utiliserons la méthode de séparation des variables $ t $ et $ x $ en posant : $ h(x,t)=X(x)T(t) $.
En injectant cette expression dans la relation précédente, il vient:
$ (8)\qquad X(x)T'(t)=X"(x)T(t) $
Les 2 variables $ t $ et $ x $ étant indépendantes, on peut écrire:
$ (9)\qquad \frac{X"(x)}{X(x)}=\frac{T'(t)}{T(t)}=-\omega^2 $
La constante $ -\omega^2 $ est négative pour s'assurer d'avoir des solutions non-nulles (Reinhard 2001). Nous retiendrons $ X"(x)=-\omega^2 X(x) $, soit $ h_{xx}=-\omega^2 h $
Pour calculer la fonction de transfert, nous utiliserons la transformée de Fourier par rapport à $ x $. Nous avons $ h_{xx}=X"T $. D'où d'après (5) et (9):
$ (10)\qquad \mathcal{F}(h_t)=\mathcal{F}(h_{xx})=\mathcal{F}(X"T)=\mathcal{F}(-\omega^2XT)=-\omega^2\mathcal{F}(XT)=-\omega^2\mathcal{F}(h) $
Or par définition, la transformée de Fourier de $ h $ s'écrit :
$ (11)\qquad \mathcal{F}(h)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty}h(x,t) e^{-i\omega x} dx $
Nous en déduisons :
$ (12)\qquad \mathcal{F}(h_t)= \frac{1}{\sqrt{2\pi}} \frac{\partial}{\partial t}\int_{-\infty}^{+\infty} h(x,t) e^{-i\omega x} dx= \frac{\partial}{\partial t}\mathcal{F}(h) $
En rapprochant (10) et (12), nous obtenons:
$ (13)\qquad \frac{\partial}{\partial t}\mathcal{F}(h)=-\omega^2\mathcal{F}(h) $
Soit:
$ (14)\qquad \frac{\dot{\mathcal{F}}(h)}{\mathcal{F}(h)}=-\omega^2 $
et en intégrant par rapport au temps dans le domaine des transformées $ (\omega,t) $:
$ (15)\qquad \mathcal{F}(h)=G(\omega)e^{-\omega^2t} $
A $ t=0 $
$ (16)\qquad \mathcal{F}(h(x,0))=\mathcal{F}(h_0(x))=G(\omega) $
Donc en remplaçant $ G(\omega) $ dans (15), il vient:
$ (17)\qquad \mathcal{F}(h)=\mathcal{F}(h_0(x))e^{-\omega^2t} $
Prenons la transformée de Fourier inverse de la fonction exponentielle:
$ (18)\qquad \mathcal{F}^{-1}(e^{-\omega^2t})=\frac{1}{\sqrt {2t} } e^{-x^2/4t} $
d'où la relation:
$ (19a)\qquad \mathcal{F}(h)=\mathcal{F}(h_0(x)).\mathcal{F}(g(x,t)) $
$ (19b)\qquad g(x,t)=\frac{1}{ \sqrt {2t} } e^{-x^2/4t} $
Sachant que le produit de deux transformées de Fourier de deux fonctions est égal à la transformée de Fourier du produit de convolution de ces deux fonctions:
$ (20)\qquad \mathcal{F}(h)=\mathcal{F}(h_0(x))\mathcal{F}(g(x,t))=\frac{1}{ \sqrt {2\pi} } \mathcal{F}(h_0*g) $
Il vient:
$ (21)\qquad h(x,t)=h_0(x)*\frac{1}{ \sqrt {4\pi t} } e^{-\frac{x^2}{4t}} $
Cette solution est la solution fondamentale de l'équation de transfert $ \mathcal{T}(x,t) $ (équation 7), qui finit par s'écrire:
$ (22)\qquadh(x,t)=\frac{1}{ 2\sqrt {\pi t} } \int_{-\infty}^{+\infty}h_0(y) \exp{\left[-\frac{(x-y)^2}{4t}\right]} dy $
Ainsi, la solution au problème de valeur initiale $ h_0(x) $ s'obtient par convolution de $ h_0(x) $ par la fonction solution fondamentale de l'équation de transfert $ \mathcal{T} $ représentée par l'équation dite de la chaleur.
Simulation de la déformation du profil d'un chenal soumis au transport solide
Nous allons résoudre l'équation (22) dans le cas de l'exemple de Fredsoe. Le domaine qui est représenté par un versant de chenal, peut être divisé en 3 sous domaines, sachant que l'origine des axes est choisi au milieu du versant droit.
Il faut rappeler que $ h_0(y) $ est la fonction définie par morceaux qui représente le profil initial du chenal (Figure 1).
- de l'infini à gauche au pied du versant (zone C à gauche)
- du pied du versant au sommet du versant (zone B)
- du sommet du versant à l'infini à droite (zone A)
$ (23)\qquad h(x,t)=\frac{1}{ 2\sqrt {\pi \nu t} } \left( -\frac {a}{2}\right) \int_{-\infty}^{-b/2} \exp{\left[-\frac{(x-y)^2}{4\nu t}\right]} dy $
$ +\frac{1}{ 2\sqrt {\pi \nu t} } \int_{-b/2}^{+b/2} \left( \frac {a} {b} y \right) \exp{\left[- \frac{(x-y)^2}{4\nu t}\right]} dy $
$ +\frac{1}{ 2\sqrt {\pi \nu t} } \left( \frac {a}{2}\right) \int_{b/2}^{\infty} \exp{\left[- \frac{(x-y)^2}{4\nu t}\right]} dy $
Ces 3 intégrales peuvent être calculées explicitement :
$ (24)\qquad h(x,t)=\frac{a}{4} \mathrm{erf} \left( \frac {x+b/2} {2 \sqrt{\nu t}} \right) -\frac{a}{4} $
$ +\frac{a}{b} \frac{\sqrt{\nu t}} {\sqrt{\pi}} \exp{ \left[ -\frac{(x+b/2)^2} {4\nu t} \right] } +\frac{1}{2} \left( \frac{ax}{b} \right) \mathrm{erf} \left[ \frac{x+b/2} { 2\sqrt{\nu t} }\right] $
$ -\frac{a}{b} \frac{\sqrt{\nu t}} {\sqrt{\pi}} \exp{ \left[ -\frac{(x-b/2)^2} {4\nu t} \right] } -\frac{1}{2} \left( \frac{ax}{b} \right) \mathrm{erf} \left[ \frac{x-b/2} { 2\sqrt{\nu t} }\right] $
$ -\frac{a}{4} \mathrm{erf} \left( \frac {x-b/2} {2 \sqrt{\nu t}} \right) +\frac{a}{4} $
après simplifications et remise en ordre, on obtient:
$ (25)\qquad h(x,t)=\mathrm{erf} \left( \frac{b/2-x} { 2\sqrt{\nu t}} \right) \left( \frac{ax}{b2} - \frac{a}{4} \right) - \mathrm{erf} \left( \frac{-b/2-x} { 2\sqrt{\nu t}} \right) \left( \frac{ax}{b2} + \frac{a}{4} \right) $
$ +\frac{a}{b} \frac{\sqrt{\nu t}} {\sqrt{\pi}} \left( \exp{ \left[ -\frac{(x+b/2)^2} {4\nu t} \right] }- \exp{ \left[ -\frac{(x-b/2)^2} {4\nu t} \right] } \right) $
Ces résultats sont identiques à ceux de Fredsoe (1978) qui n'avait pas explicité son raisonnement et dont les formules présentent quelques coquilles d'impression.
Comparaison avec les essais physiques
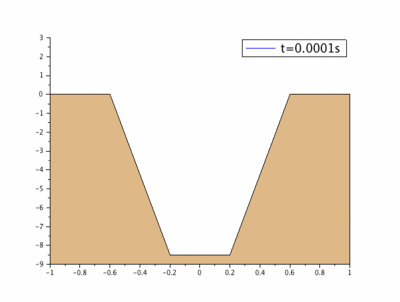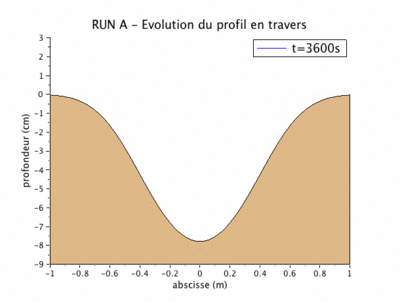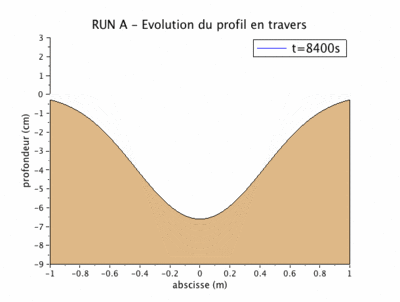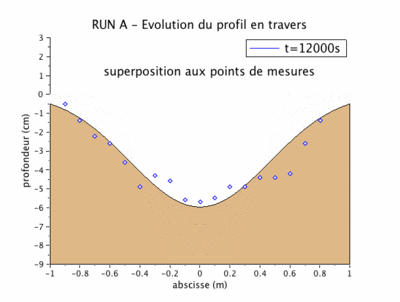
Nous avons repris les résultats des essais physiques publiés par Fredsoe et avons superposé les résultats du modèle mathématique obtenu précédemment.
Nous reprendrons ici les résultats obtenues pour deux expériences : les run A et run B.
Run A après 200 mn
Les paramètres précédemment définis nous conduisent aux valeurs du débit solide $ q_b=1.9.10^{-6} m^2/s $ et du coefficient de "diffusion" $ \nu=6.78.10^{-6} m^2/s $.
La figure suivante superpose le profil obtenu par le modèle numérique et par le modèle physique au bout de 200 mn.
Par ailleurs, la déformation du fond peut être visualisée en consultant la page WIKHYDRO : ANSWER Saint-Brévin
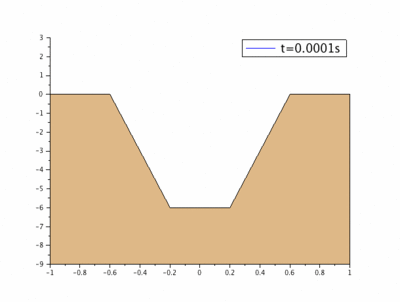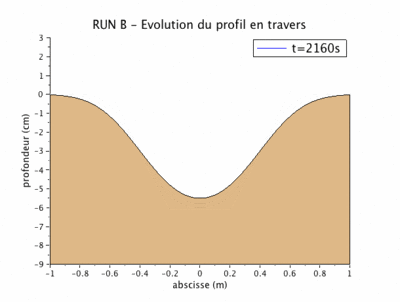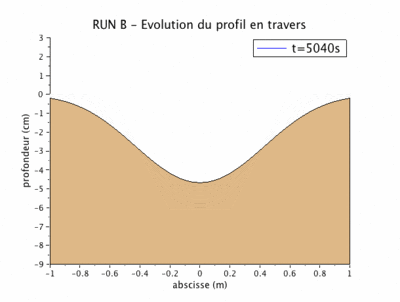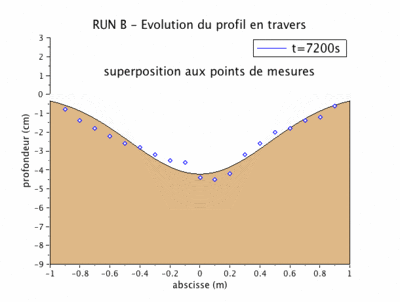
Run B après 120 mn
Les paramètres précédemment définis nous conduisent aux valeurs du débit solide $ q_b=3.2.10^{-6} m^2/s $ et du coefficient de "diffusion" $ \nu=11.4.10^{-6} m^2/s $.
La figure suivante superpose le profil obtenu par le modèle numérique et par le modèle physique au bout de 120 mn.
Par ailleurs, la déformation du fond peut être visualisée en consultant la page WIKHYDRO : ANSWER Saint-Brévin
Analyse des résultats
La comparaison des résultats du modèle avec les mesures sur modèle physique pour les run A et run B montre quelques différences expliquées par Fredsoe par les considérations suivantes:
- la tendance au méandrement de l'écoulement provoque la non symétrie obtenue sur le modèle physique;
- le modèle mathématique a été bâti en considérant un transport solide constant et uniforme sur l'ensemble du domaine. Or le gabarit trapézoïdal du chenal s'accompagne d'une profondeur variable le long de la section. Dans la configuration du run A par exemple, la profondeur passe de 0 à -8.5 cm (fond du chenal) pour une profondeur d'eau de +50 cm. Cette approximation est de nature à provoquer quelques non-symétries.
Nous pouvons également rajouter le point suivant :
- la perturbation hydrodynamique produite par la présente de rides dont les hauteurs atteignent 2,5 cm en fin d'expérience n'est pas prise en compte dans le modèle
Conclusion
La linéarisation de l'équation de transport, obtenue en considérant le transport solide comme uniforme dans la section du chenal permet d'obtenir un modèle mathématique du 2ème ordre (équation de diffusion ou équation de la chaleur).
La résolution de ce modèle permet d'obtenir une solution analytique qui, comparée aux 2 expérimentations (run A et run B) conduites par Fredsoe (1978), fournit une bonne représentativité du comportement du profil en travers du chenal au cours du temps.
Ceci valide l'hypothèse d'un transport longitudinal permanent et d'un transport dans le profil conservatif dû à la gravité.
Le modèle mathématique obtenu peut donc être tout à fait utilisé pour générer des solutions analytiques qui rentrent dans les cahiers de cas test d'un modèle d'évolution morphodynamique bidimensionnel.
En ce qui concerne les méthodes d'analyse numérique, nous avons tout particulièrement mis en œuvre:
- la transformée de Fourier
- le produit de convolution
Références
- Reinhard H., "Équations aux dérivées partielles - Introduction", Dunod, 2001, 291 p.
- Hamm L., Tanguy J.M., Zhang B.N., "Prise en compte des effets gravitaires dans la modélisation du transport solide par charriage", La Houille Blanche, N. 4/1994, pp 47-55.
- Van Rijn L.C., "Hansbook sediment transport by currents and waves"Delft Hydraulics report H461.
- Latteux B., Hamm L., "Inclusion of bottom slope effects in modelling bed-load tranport under steady flow". EuroMech 310, 13-17 sept. 1993, Le Havre France.
- Fredsoe, J., "Sedimentation of River Navigation Channels", Journal of the Hydraulics Division, ASCE, Vol. 104, N. HY2, February 1978, pp. 223 - 236.
- Engelund, F.,"Flow and Bed Topography in Channel Bends", Journal of the Hydraulics Division, ASCE, Vol. 100, Num. HY11, Proc. Paper 10963, Nov. 1974, pp 1631-1648.
- Engelung, F. and Hansen, E., "A Monograph on Sediment Transport in Alluvial Streams", Danish Technical Press, Copenhagen, Denmark, 1972
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS