ANSWER - Modèle de propagation des ondes longues
Eléments de contexte
Cette page fait partie de la démarche collaborative ANSWER , dont l'objectif est créer les conditions de collaboration entre scientifiques et grand public autour du domaine de l'eau.
Quatre sous-domaines ont été identifiées : hydraulique fluviale, hydraulique maritime, hydrogéologie et morphodynamique.
Cette page fait partie du sous-domaine hydraulique maritime.
La marée en haute mer
Comment se propage la marée
Observation en nature
Des photos ou des vidéos enregistrées en nature peuvent donner une vision dynamique et réaliste du phénomène de marée.
Essais en laboratoire
Des essais en laboratoire peuvent être envisagés pour reproduire partiellement ce phénomène.
Modélisation mathématique des phénomènes de transport - évolution des fonds
Hiérarchie des hypothèses simplificatrices
Navier-Stokes
- → fluide incompressible
- → intégration dans une section de calcul (canal rectangulaire) ==> Saint-Venant 1D
- → accélération négligeable
- → frottement négligeable
- → accélération négligeable
- → intégration dans une section de calcul (canal rectangulaire) ==> Saint-Venant 1D
Expression de l'équation simplifiée
A partir des hypothèses précédentes, considérons un canal infini de forme rectangulaire : largeur $ b $ et profondeur d'eau $ H $.
Soit $ h $ le niveau d'eau, $ u $ la vitesse moyenne de l'écoulement dans la section de surface $ A = bH $ et enfin $ Q=bHu $ le débit.
Les équations simplifiées prennent la forme suivante :
$ \begin{cases} \dfrac{ \partial h }{ \partial t }+H \dfrac{ \partial u }{ \partial x }=0 } \\ \\ \dfrac{ \partial u }{ \partial t }+g \dfrac{ \partial h }{ \partial x }=0 \end{cases} $
Si l'on dérive la première équation par rapport à $ t $ et la seconde par rapport à $ x $, et en éliminant le terme $ \dfrac{ \partial^2 u }{ \partial x \partial t } $, nous obtenons l'équation des ondes suivante: $ \dfrac{ \partial^2 h }{ \partial t^2 }-gH \dfrac{ \partial^2 h }{ \partial x^2 }=0 $
Solution analytique
Cette équation peut se mettre sous la forme:
$ (\dfrac{ \partial h }{ \partial t }-c \dfrac{ \partial h }{ \partial x }) ( \dfrac{ \partial h }{ \partial t }+c \dfrac{ \partial h }{ \partial x })=0 $
Une solution de cette équation pour l'évolution de la surface libre est la suivante:
$ h=acos(kx-\sigma t) $
qui correspond à la propagation de 2 ondes de vitesse $ c= \sqrt{gH} $ dans les deux sens (vers la gauche et vers la droite)
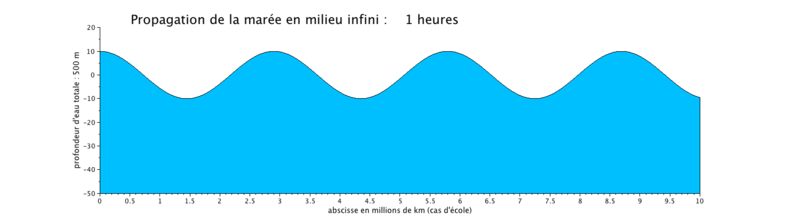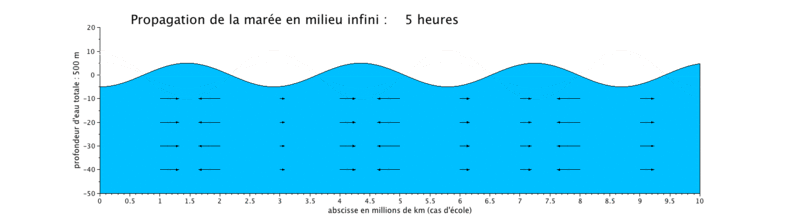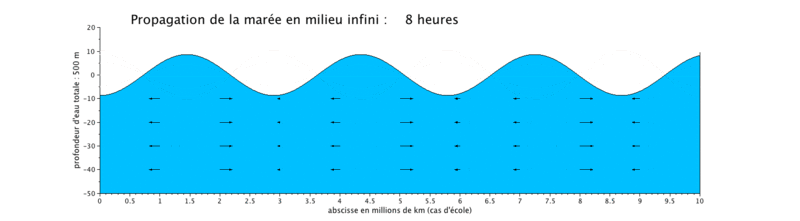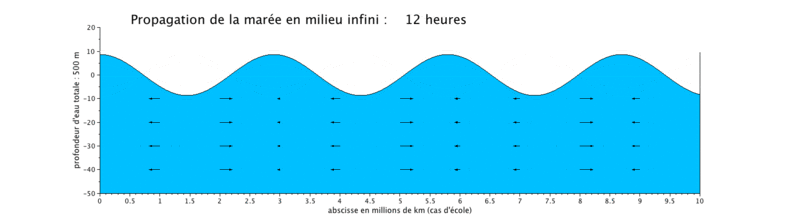
Cas d'application : translation d'une onde sinusoïdale
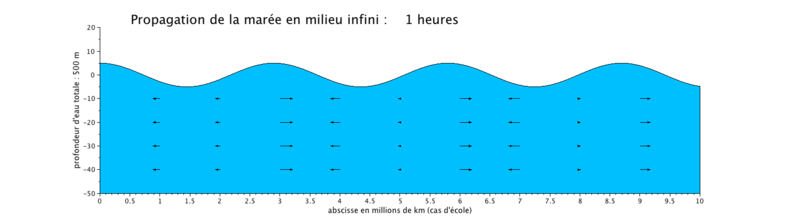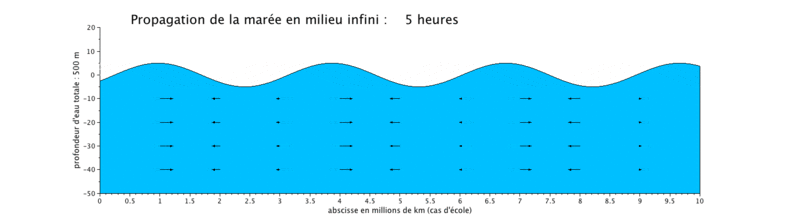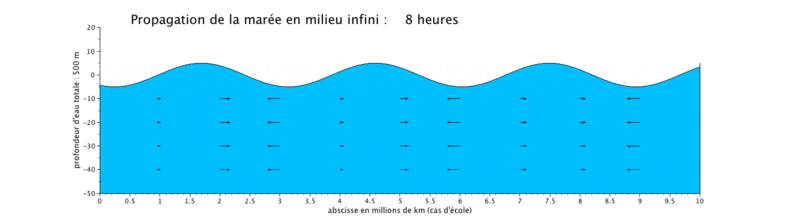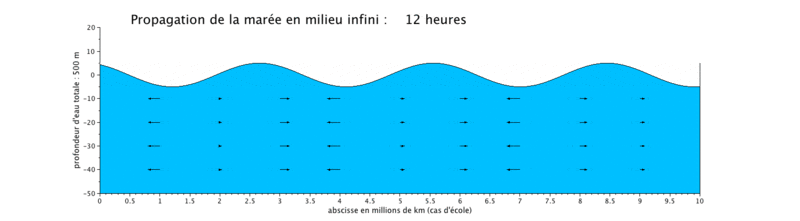
Onde de marée progressive
Le cas que nous présentons ici est un cas d'école, car il met en scène la propagation d'une onde de marée de période de 12 heures dans un canal infini (ici limité à $ 10^7 $ m, ceci pour illustrer plusieurs longueurs d'onde sur une même figure).
Les caractéristiques de cet exemple sont les suivants:
- période de la marée : 12 heures
- amplitude : 5m
- profondeur : 500 m (la profondeur sur les représentations graphiques a été limitée à 50 m pour des questions de lisibilité)
Les calculs conduisent à:
- longueur d'onde : 32 102 003 m
- célérité : 70 m/s
- nombre d'onde : 2,077E-006 m-1
Le champ de vitesse peut être obtenu en remplaçant l'expression de la surface libre $ h(x,t) $ dans l'équation de continuité. En dérivant l'expression de $ h(x,t) $ par rapport à $ t $ et en l'intégrant par rapport à $ x $, nous obtenons l'expression de la vitesse:
$ u=\dfrac{ a\sigma }{ k H} \cos(kx-\sigma t)=\dfrac{ a\sqrt g }{ \sqrt H} \cos(kx-\sigma t) $
Onde de marée stationnaire
Le cas de l'onde marée stationnaire correspond à la rencontre de deux ondes de même période mais de sens opposé. Ces deux ondes ont les caractéristiques précédentes.
Les expressions de la variation du niveau d'eau et de la vitesse sont les suivantes:
$ h=2a \cos kx \cos\sigma t $
$ u=2\dfrac{ agk}{ \sigma } \sin kx \sin\sigma t $
Remarquons que dans ce cas, niveau d'eau et vitesse sont en opposition de phase.
Essai en laboratoire
Des essais en laboratoires peuvent être envisagés en respectant la similitude de Froude.
Observation en nature
Des videos en nature ou des résultats de modèles numériques sur le propagation de la marée (marée en Manche par exemple) ou de résonance (Baie de Fundy au Canada) pourraient donner une vision dynamique et réaliste du phénomène.
Conclusions
D'après les exemples précédents, nous pouvons mettre en évidence les processus suivants:
- la propagation de l'onde progressive se fait avec une vitesse de courant en phase avec le niveau d'eau, ce qui signifie que lorsque le niveau d'eau est maximal, c'est-à-dire en haute mer (respectivement minimal en basse mer), la vitesse du courant est maximale (respectivement minimale). Les vitesses sont minimales à mi-montant et à mi-perdant. Ceci se produit donc en haute mer.
- par contre, et c'est vraiment ce qui se passe dans les estuaires, la situation est complètement opposée pour l'onde stationnaire. Dans ce cas, niveau d'eau et vitesse sont en opposition de phase. Ainsi, lorsque le niveau est maximal (pleine mer) ou minimal (basse mer), les vitesses sont nulles. Ces vitesses sont maximales à mi-montant et à mi-perdant.
- plusieurs auteurs (Le Méhauté, 1976) ont considéré que la théorie des ondes longues pouvait être considérée comme la limite de la théorie de la propagation des ondes en eaux profondes. Ceci était probablement justifié par l'équation de la surface libre qui est dans les deux cas de la forme $ h=acos(kx-\sigma t) $. La similitude s'arrête là, car le patron des vitesses est très différent : très rapidement dégressif pour les ondes de surface et constant dans toute la verticale et jusqu'au fond pour les ondes longues. Enfin, il n'y a pas de transfert de masse pour les ondes de surface alors qu'il y en a pour les ondes longues.
Bibliographie
- Le Méhauté B., "An Introduction to Hydrodynamics & Waterways" Springer-Verlag, 1976, 315 p.
- Thual O., "Hydrodynamique de l'environnement", Les éditions de l'Ecole Polytechnique, Oct. 2011, 314 p.
- Dinguemans M. W., "Water Wave Propagation Over Uneven Bottoms - Part 1 - Linear Wave Propagation", Advanced Series on Ocean Engineering - Volume 13, World Scientific, 471 p.
- Dinguemans M. W., "Water Wave Propagation Over Uneven Bottoms - Part 2 - Non-Linear Wave Propagation", Advanced Series on Ocean Engineering - Volume 13, World Scientific, 494 p.
- site du SHOM et plus particulièrement une page dédiée aux courants de marée
code Scilab
Les animations précédentes ont été réalisées à l'aide le l'application SCILAB.
Elles peuvent être utilisées pour reproduire le graphique. Il suffit de sélectionner l'ensemble du texte dans le fichier *.pdf et de le copier dans l'éditeur du logiciel puis d'exécuter le programme.
Le fichier est disponible ici : Fichier:Marée progressive et stationnaire.pdf
Nous sommes bien entendu preneurs de toute amélioration du code source.
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS