ANSWER - Tide propagation in a sloping bottom converging banks estuary
Context
Version française
This page is part of the collaborative approachANSWER , whose goal is to make scientists and general public collaborate in the field of water.
This sheet is a continuation of the "Propagation d'une onde dans un estuaire à pente du fond inclinée" but deals with the propagation of a wave in an estuary with a rectangular section whose section narrows linearly upstream and whose slope of the bottom is also linear.
Mathematical modeling of wave propagation phenomenon in an estuary
We will start from the one-dimensional Saint-Venant equations system, which will have been linearized to study the deformation of a wave during its propagation along a schematic estuary.
The linearization of this system will lead to an equation that will be solved directly, thus providing the temporal variation of the water level and the average celerity per section.
We will study 4 configurations:
- frictionless propagation with upstream boundary condition of open exit
- total reflection at the downstream boundary of the estuary and propagation without friction
- propagation with slight friction and upstream boundary condition of open exit
- propagation with strong friction and upstream boundary condition of open exit
We will take into account in this example a channel of rectangular section which narrows from downstream (the sea) to upstream (the river), a constant linear slope ascending towards the bottom and a convergence of the banks.
We will compare the results obtained by these analytical solutions with those obtained with TELEMAC2D two-dimensional finite element hydrodynamic computation code.
Hierarchy of simplifying hypotheses
The simplifications that follow allow us to develop a linear model of propagation of a wave within a simplified geometry domain, corresponding to a bottom slope canal, which can approach a schematic inside which spreads a surge wave.
'Navier-Stokes'
- → incompressible fluid
- → integration in a calculation section (rectangular channel) ==> Saint-Venant 1D
- → negligible acceleration
- → linearized friction
- → negligible acceleration
- → integration in a calculation section (rectangular channel) ==> Saint-Venant 1D
Expression of the simplified model
From the above assumptions, consider a rectangular cross-sectional channel with a constant bottom slope and a constant bank convergence rate.
Soit :
- $ h(x,t) $ water level
- $ u(x,t) $ flow mean velocity of the flow in the section $ S(x)=b(x)H(x) $
- $ Q(x,t)=S(x,t)u(x,t) $ discharge at section $ x $
- $ b(x)=b_0\dfrac{ x }{ x_0 } $ canal width which varies linearly with the abscisse, $ b_0 $ is the canal width at abscisse $ x_0 $ upstream of the estuary. $ p_b=b_0/x_0 $
- $ H(x)=H_0\dfrac{ x }{ x_0 } $ canal depth which varies linearly with the abscisse. $ p_f=H_0/x_0 $
- $ f $ linearized roughness coefficient
The equations governing the phenomenon are the linearized 1D Saint-Venant equations:
$ \begin{cases} b\dfrac{ \partial h }{ \partial t }+ \dfrac{ \partial Q }{ \partial x }=0 } \\ \\ \dfrac{ \partial Q }{ \partial t }+gS \dfrac{ \partial h }{ \partial x }+fQ=0 \end{cases} $
Deriving the first equation with respect to time and the second with respect to space and eliminating the common term, we obtain:
$ -b\dfrac{ \partial^2 h }{ \partial t^2 }+ g\dfrac { \partial }{ \partial x }\left[\Big S\dfrac{ \partial h }{ \partial x }\right]\Big +f\dfrac{ \partial Q }{ \partial x}=0 $
we are going to suppose that $ h $ is of the form $ h=A(x)e^{-i\sigma t} $. Deriving, we obtain :
$ \dfrac{ \partial h }{ \partial t}=(-i\sigma) A(x) e^{-i\sigma t} = -i\sigma h \qquad et \qquad \dfrac{ \partial^2 h }{ \partial t^2}=-\sigma^2 h $
By reporting these values in the equation above :
$ x^2\dfrac{ \partial^2 h }{ \partial x ^2}+2x\dfrac{ \partial h }{ \partial x} + \left[\Big \sigma (\sigma+fi) \right] \dfrac{ 1}{gp_f}} xh=0 $
Posons:
$ k^2=\dfrac{ \sigma^2}{ gH} \text{ wave number et }<br /> k_f^2=\sigma (\sigma+fi) \dfrac{ x_0}{ gH_0}\right] $
This term is a constant
Moreover, the friction can be expressed as follows :
$ f=\dfrac{8}{3\pi}\dfrac{g}{K^{2}{H_m^{4/3}}}\left| U_m \right| $ avec :
- $ K $ is the Strickler coefficient close to 0.002 - 0.003
- $ H_m $ the mean depth
- $ U_m $ the mean speed on a period
'Note' : this equation shows us that the distribution of the wave height is independent of the linear convergence rate of banks $ p_b $, but depends on the height of the water average $ H_0 $.
Analytical solution
We recognize a Bessel type equation:
$ x^2y''+(2p+1) x y'+(\alpha^2x^{2r}+\beta^2)y=0 $
The solution of this equation is given by:
$ y=x^{-p} \left[ c_{1} J_{P/r} (\alpha x^{r}/r) + c_{2} Y_{P/r} (\alpha x^{r}/r) \right] $
The fonctions $ J_{P/r} $ and $ Y_{P/r} $ are fonctions de Bessel first and second kind respectively.
In our case, we have : $ p=1/2, \beta=0, \alpha^2=k_f^2 , r=1/2 $ with $ P=\sqrt{p^2-\beta^2}=0 $
where:
$ h(x)=\dfrac{ 1 } { \sqrt x} \left[ c_{1} J_{1} (2k_f\sqrt x)+c_{2} Y_{1} (2k_f\sqrt x) \right]e^{-i\sigma t} $
The equation of momentum allows us to calculate the velocity $ u(x,t): $
$ b\dfrac{ \partial h } { \partial t}+\dfrac{ \partial }{ \partial x} (bHu)=0<br /> $
also:
$ bHu=i\sigma \dfrac{ b_0 } { x_0}e^{-i\sigma t} \int_{x} \sqrt x \left[ c_{1} J_{1} (2k_f \sqrt x)+c_{2} Y_{1} (2k_f \sqrt x) \right]\, \mathrm dx $
Given: $ z=2k_f \sqrt x $, il vient : $ dz=k_f \dfrac{1}{\sqrt x} dx $ et $ dx= \dfrac{z}{2k_f^2}dz $
By substituting these expressions in the previous equation, we obtain:
$ bHu= \dfrac{ b_0 } { x_0} \dfrac{ i\sigma} { 4k_f^3} e^{-i\sigma t} \int_{x} z^2 \left[ c_{1} J_{1} (z)+c_{2} Y_{1} (z) \right]\, \mathrm dz $
To calculate this integral, we use the following recurrence relation:
$ \dfrac{d}{dx} (x^n J_{n}(x))=x^n J_{n-1}(x) $, the same for $ Y_{n}(x) $
We obtain :
$ u=i\sigma \dfrac{ 1} { k_f} \dfrac{x_0} { H_0} \dfrac{1} { x} \left[ c_{1} J_{2} (2k_f \sqrt x )+c_{2} Y_{2} (2k_f \sqrt x ) \right] e^{-i\sigma t} $
Summary: expression of the final analytical solution
In summary, the analytical expression expressing the variation of the water level and the mean velocity in any section of the domain are given by the following equations:
$ h(x,t)=\Re \Bigl(\left \dfrac{ 1} { \sqrt x} [ c_{1} J_{1} (2k_f \sqrt x)+c_{2} Y_{1} (2k_f \sqrt x) \right] e^{-i\sigma t}\Bigr) $
$ u(x,t)=\Re \Bigl( i\sigma \dfrac{ 1} { k_f} \dfrac{x_0} { H_0} \dfrac{1} { x} \left[ c_{1} J_{2} (2k_f \sqrt x) + c_{2} Y_{2} (2k_f \sqrt x) \right] e^{-i\sigma t}}\Bigr) $
Starting from the general expressions of $ h(x,t) $ et de $ u(x,t) $, we can determine the solution by setting 2 boundary conditions. We will consider the following two cases:
- propagation of an incoming wave from downstream (right) to upstream of the domain with open boundary condition at the upstream end (left)
- reflection of the same incoming wave from downstream (right) to upstream with total reflection at the upstream end (left)
Configuration n°1 : estuary without roughness - radiation boundary condition
We impose 2 boundary conditions to determine the two integration constants.
- an entering boundary condition at the entrance from the right side $ h(x_1,t)=A(x_1,t) e^{-i\sigma t}=a(x_1,t)e^{i(kx_1 -\sigma t)}=a(x_1,t)e^{i\phi} \quad\forall t $
- an exit boundary condition of Sommerfeld radiation type :
$ h(x,t)=a(x_0) e^{i\phi } $
Deriving this expression, we get:
$ \dfrac{ dh }{ dx }=e^{i\phi}\dfrac{ da }{ dx }+iae^{i\phi}\dfrac{ d\phi }{ d x } $
Each term expresses a process:
- taking into account shoaling : $ \dfrac { d a }{ d x }=- \dfrac { 1 }{ 4 } \dfrac { p_0 }{ H } a $. The slope being zero, the shoaling term is canceled.
- eikonale equation : $ \dfrac{ d\phi }{ d x }=k $($ k $ is the wave number)
We get:
$ \dfrac{ d h }{ d x }= ae^{i\phi}(-\dfrac{1}{4}\dfrac{p_0}{H}+ik) $
or:
$ \dfrac{ d h }{ d x }= A(x,t)e^{-i\sigma t}(-\dfrac{1}{4}\dfrac{p_0}{H}+ik) $
sand:
$ (1) \qquad \dfrac{ d A }{ d x }= A(x,t)(-\dfrac{1}{4}\dfrac{p_0}{H}+ik) $
and
$ A=\dfrac{1}{\sqrt x}\Big( c_{1} J_{1} (2k_f \sqrt x )+c_{2} Y_{1} (2k_f \sqrt x ) \Big) $
Deriving this expression, we get.:
$ (2) \qquad \dfrac{dA}{dx}=-\dfrac{1}{2}\dfrac{1}{x\sqrt x }\Big[c_{1} J_{1} (2k_f \sqrt x )+c_{2} Y_{1} (2k_f \sqrt x ) \Big] - \dfrac{k_f}{x} \Big[ c_{1} J_{2} (2k_f \sqrt x )+c_{2} Y_{2} (2k_f \sqrt x ) \Big] $
knowing that :
$ \dfrac {d } {dz} J_{1}(z) =- J_{2} (z)\quad \text{et}\quad \dfrac {d } {dz} Y_{1}(z) =- Y_{2} (z) $
Applying relation (2) at $ x=x_0 $ and stating :
$ \gamma =-\dfrac{1}{2 }-ikx_0 \qquad\text {et} \qquad \delta=-k_f \sqrt x_0 $
We get the following system to solve to calculate the coefficients :$ c_{1} \text {et} c_{2} $
$ \begin{cases} c_{1} ( \gamma J_{1}^0 + \delta J_{2}^0 )+ c_{2}( \gamma Y_{1}^0 + \delta Y_{2}^0 )=0 \\ \\ c_{1}J_{1}^1 +c_{2}Y_{1}^1 =A_1 \sqrt x_1 \end{cases} $
This leads to the following solution :
$ \begin{cases} D=( \gamma J_{1}^0 + \delta J_{2}^0 ) Y_{1}^1 - ( \gamma Y_{1}^0 + \delta Y_{2}^0 )J_{1}^1 \\ D_{c_1}=-A_1\sqrt {x_1}( \gamma Y_{1}^0 + \delta Y_{2}^0 ) \\ D_{c_2}=A_1\sqrt {x_1} ( \gamma J_{1}^0 + \delta J_{2}^0 ) \\ c_1=D_{c_1}/D \qquad c_2=D_{c_2}/D \\ h(x,t)=\Re \Bigl(\left \dfrac{ 1} { \sqrt x} [ c_{1} J_{1} (2k_f \sqrt x)+c_{2} Y_{1} (2k_f \sqrt x) ] e^{-i\sigma t}\Bigr) \\ u(x,t)=\Re \Bigl( i\sigma \dfrac{ 1} { k_f} \dfrac{x_0} { H_0} \dfrac{1} { x} \left[ c_{1} J_{2} (2k_f \sqrt x) + c_{2} Y_{2} (2k_f \sqrt x) \right] e^{-i\sigma t}}\Bigr) \end{cases} $
'Application case: translation of a sinusoidal wave'
The characteristics of this example are as follows:
- length of the canal: 10,000 km
- tide period: 900s
- amplitude: 1 m upstream
- bottom slope: 0.0001 m / m
- depth at the entrance to the downstream channel: 100 m and at its outlet upstream: 20 m
The following animation represents the propagation of a 12-hour tidal wave in an estuary whose bottom rises linearly and the banks converge linearly.
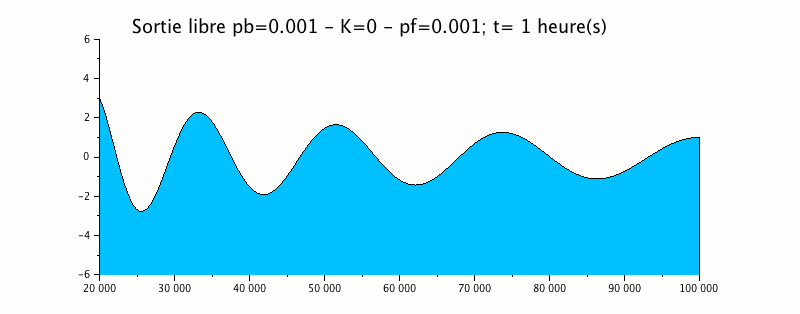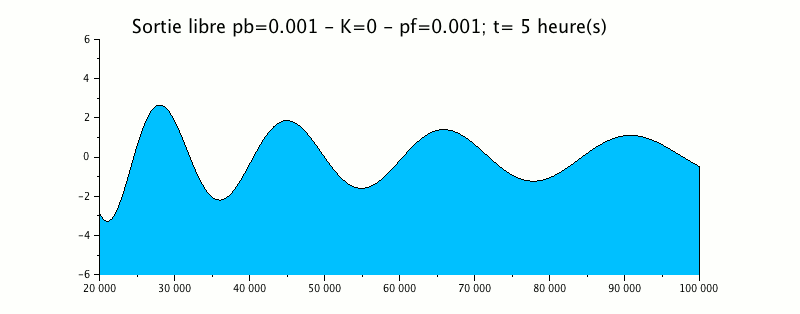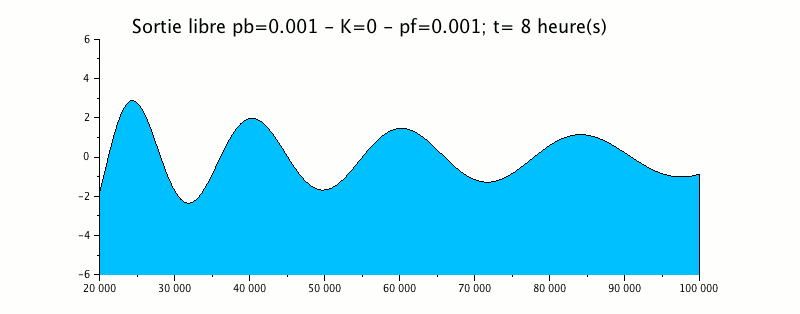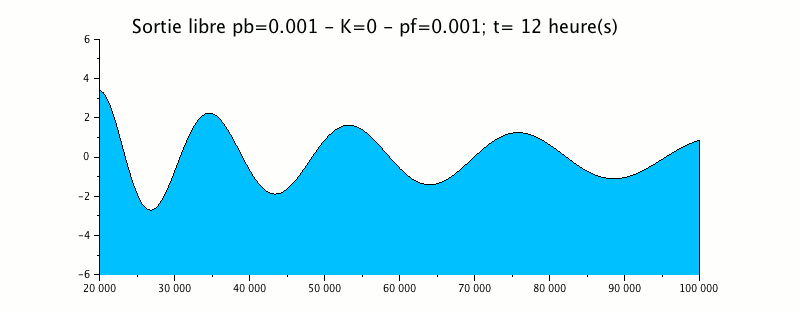
|

|
This example shows that the wave generated downstream (right on the diagram) with an amplitude of 1m propagates upstream (left) while deforming: decrease of the wavelength, increase of the amplitude.
At the left end, this wave leaves the domain without generating a reflection wave, which validates the free output condition used here.
The term shoaling introduced is of an order of magnitude less than the term eikonal and produces no significant change in the exit of the wave.
Moreover, the envelope curve clearly shows an amplification of the signal in the upstream direction.
Configuration n°2 : estuary without roughness - reflection of a wave inside the domain : linearly converging banks and sloping bottom
Let's introduce the following boundary conditions, which correspond to :
- a downstream boundary condition which generates an entering wave inside the domain from the right $ h(x_1,t)=A_1(x_1,t) e^{-i\sigma t}\quad\forall t $
- an upstream total reflective boundary condition $ u(x)=0 \quad\forall t $
We get the following system :
$ \begin{cases} c_1 J_{2}^0+c_2 Y_{2}^0 =0 \\ \\ c_1 J_{1}^1+c_2 Y_{1}^1 =A_1 \sqrt {x_1} \end{cases} $
Whose resolution leads to:
$ \begin{cases} D= J_{2}^0 Y_{1}^1 - J_{1}^1 Y_{2}^0 \\ D_{c_1}=-A_1\sqrt x_1 Y_{2}^0 \\ D_{c_2}=A_1\sqrt x_1 J_{2}^0 \\ c_1=D_{c_1}/D \qquad c_2=D_{c_2}/D \\ h(x,t)=\Re \Bigl(\left \dfrac{1} { \sqrt x} [ c_{1} J_{1} (2k_f \sqrt x)+c_{2} Y_{1} (2k_f \sqrt x) \right] e^{-i\sigma t}\Bigr) \\ u(x,t)=\Re \Bigl( i\sigma \dfrac{ 1} { k_f} \dfrac{x_0} { H_0} \dfrac{1} { x} \left[ c_{1} J_{2} (2k_f \sqrt x) + c_{2} Y_{2} (2k_f \sqrt x) \right] e^{-i\sigma t}}\Bigr) \end{cases} $
We verify that $ h(x_1,t) = A_1 e^{-i\sigma t} $
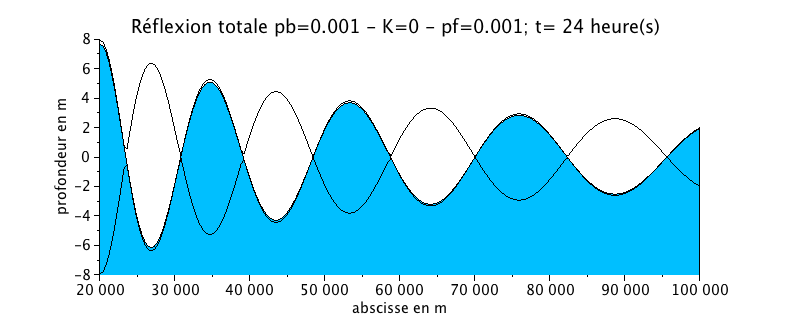
'Application case: reflection of a sinusoidal wave'
The same case as above is used, but imposing a total reflection boundary condition. In this case, a reflected wave of the same period, the same amplitude but opposite direction of propagation is superimposed on the incident wave. This is equivalent as to impose twice the amplitude of the incident wave at the "sea" boundary.
[[ ]] ]]
|
|
This animation shows the formation of regular crest and troughs which represents a total reflection.
The wavelength decreases progressively upstream as a function of the height of water. There is also an increase in the amplitude upstream.
Thus, in the absence of any friction, the wave propagates without loss of energy under the effect of the contraction of the banks and the slope of the bottom (to be compared with the similar case without slope where no deformation is observe).
Comparaison with numerical model TELEMAC2D
Propagation d'une onde dans un estuaire à pente... par Wikhydro
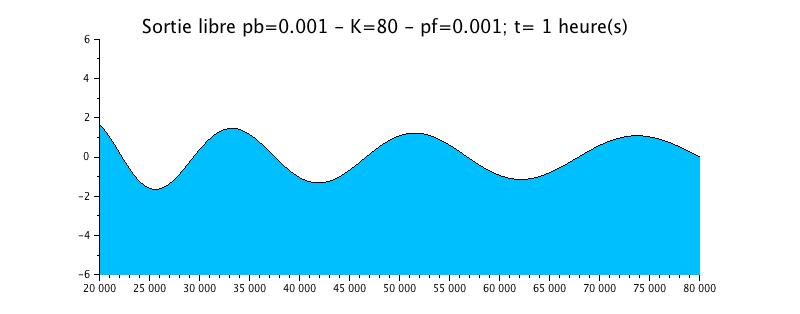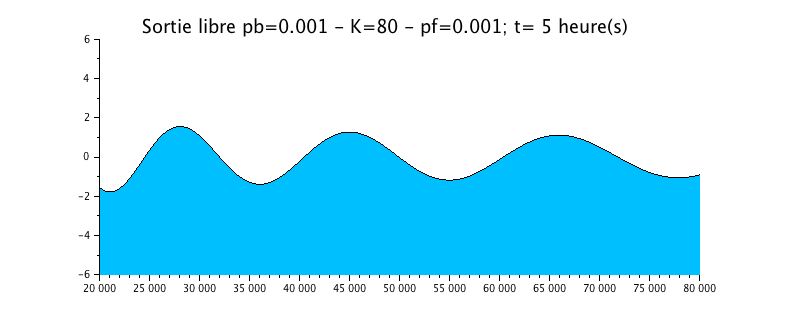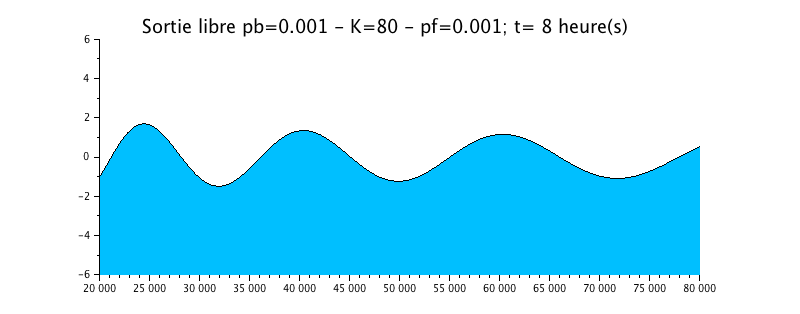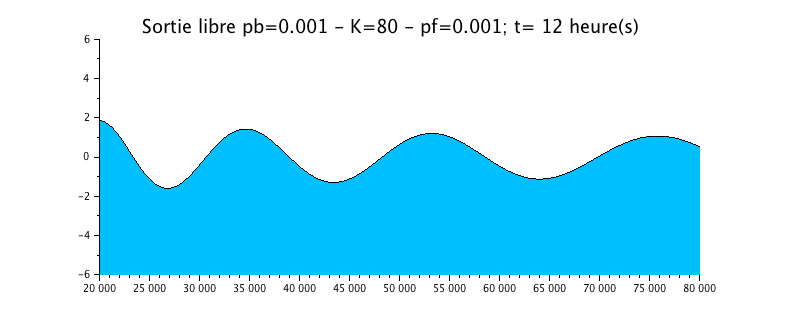
Configuration n°3 : HYPERSYNCHRONE ESTUARY with roughness / K=80
We take the previous case of the wave propagation with a radiation condition, but we add a little roughness in the form of a Strickler coefficient of 50.
|

|
The animation shows a effective but small effect on the evolution of the water level. This one is still slightly damped compared to the solution without friction (configuration n ° 1).
The envelope curve shows the signal amplification effect upstream (left)
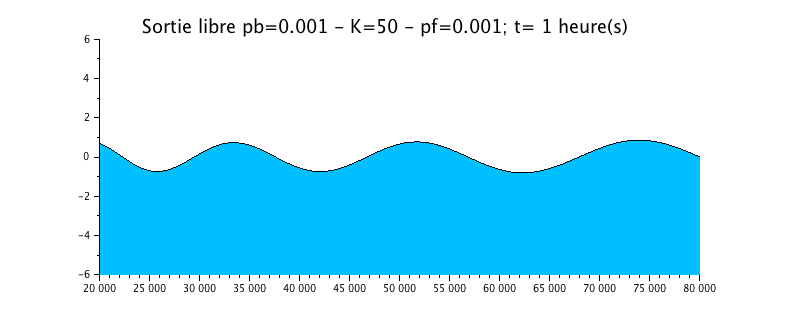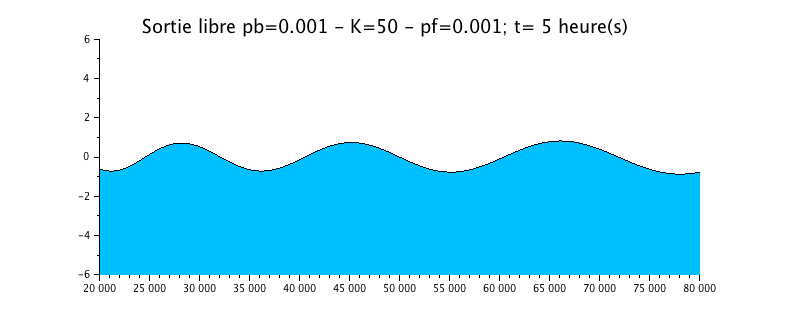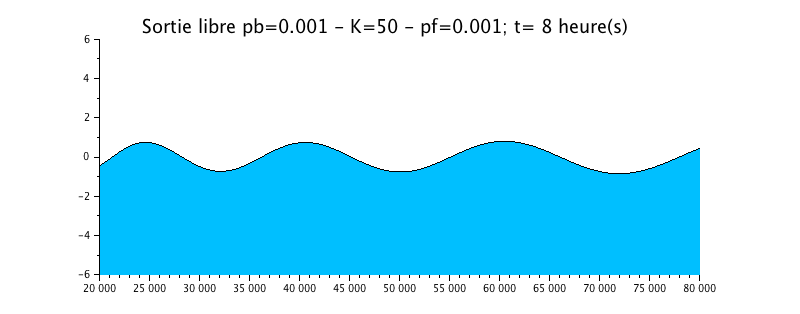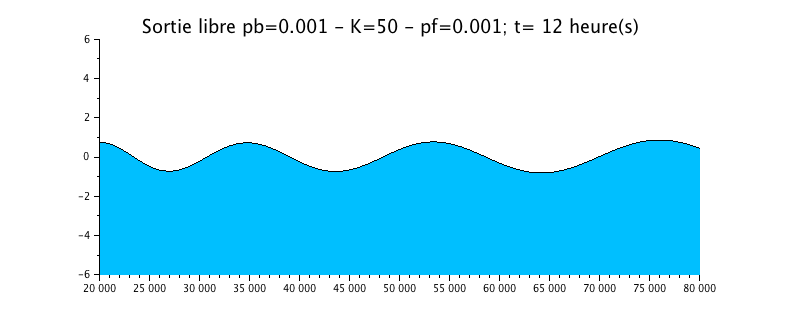
Configuration n°4 : HYPOSYNCHRONE ESTUARY with roughness / K=50
We have taken the previous case of the propagation of the wave with a radiation boundary condition exit, but we added a little more friction in the form of a Strickler coefficient of 50.
|
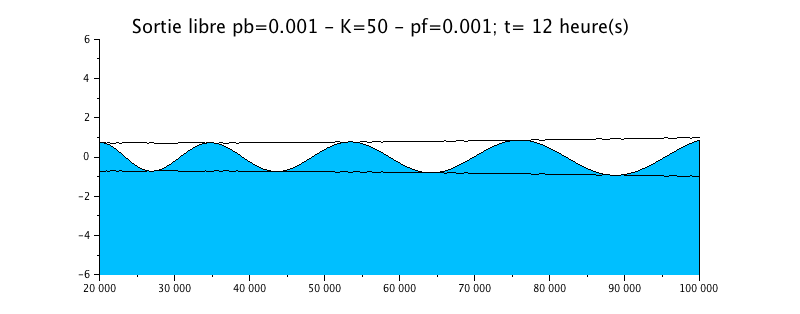
|
The animation shows a effective effect, more important than in the previous case on the evolution of the water level. This one is much more damped compared to the solution without friction (configuration n ° 1).
The envelope curve shows a clear attenuation of the signal upstream, which makes the estuary hyposynchronous.
General conclusion on the simulation of the propagation of a wave in an estuary with linearly sloping bottom and linearly decreasing section
The works consist in the derivation of the equations that represent the entry of a wave in an estuary characterized by a linearly sloping bottom and whose banks converge linearly in the upstream direction.
Several lessons can be drawn from these results:
- the boundary condition of radiation of Sommerfeld give all satisfactions: one quit the upstream boundary without generating reflection waves inside the domain
- the condition of total reflection imposed at the upstream entrance of the estuary (river side) is well represented by the analytical solution. On the other hand, the use of the numerical code also generates a reflection wave inside the domain which is superimposed on the upstream boundary condition and harms to the correct restitution, even going as far as exploding the model. A remark is necessary here on what exactly is represented with the boundary condition. If one wants to represent the superposition of the incident wave and the reflected wave, it is necessary to double the wave amplitude at the boundary condition. Thus, we see here that the enrichment of the two methods is reciprocal.
- taking into account the friction term, even linearized, is also very instructive. First of all, it must be remembered that without friction, the estuary is HYPERSYNCHRONE, because of its upward slope and its converging banks. If we add a little friction (K = 80), the wave decreases, which is in line with the theory. On the other hand, if the friction increases, the wave train is much more damped in amplitude, causing even the estuary to become HYPOSYNCHRONE.
Bibliographie
- Le Méhauté B., "An Introduction to Hydrodynamics & Waterways" Springer-Verlag, 1976, 315 p.
- Thual O., "Hydrodynamique de l'environnement", Les éditions de l'Ecole Polytechnique, Oct. 2011, 314 p.
- Dinguemans M. W., "Water Wave Propagation Over Uneven Bottoms - Part 1 - Linear Wave Propagation", Advanced Series on Ocean Engineering - Volume 13, World Scientific, 471 p.
- Dinguemans M. W., "Water Wave Propagation Over Uneven Bottoms - Part 2 - Non-Linear Wave Propagation", Advanced Series on Ocean Engineering - Volume 13, World Scientific, 494 p.
- Tanguy J.M. "Traité d'hydraulique environnementale", vol.2, "processus maritimes", reps. publi. JM Tanguy, Ed. Hermès - Lavoisier, 2010.
- site du SHOM et plus particulièrement une page dédiée aux courants de marée
- D. Prandle and M. Rahman, "Tidal Respo,se in Estuaries" Journal of the Physical Oceanography, Vol. 10, pp 1552 - 1573, 1980
Code Scilab
The previous animations were made using the SCILAB application.
They can be used to reproduce the graph. Just select all the text in the * .pdf file and copy it to the software editor and run the program.
The file is available here : Fichier:Estuaire avec correction.pdf provides the SCILAB code of the program of the previous animations.
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS
