ANSWER - flume experiment - wave propagation in estuary
Context
French Version
This page is part of the collaborative initiative ANSWER relative to the elaboration and dissemination of scientific knowledge in water resources
It concerns the following topics:
- MARITIME HYDRAULICS
- WAVE PROPAGATION IN ESTUARY
It is closely related to 2 others pages:
- Propagation d'une_onde dans un estuaire à pente du fond inclinée
- Propagation de la marée dans un estuaire à fond pentu et aux berges convergentes linéaires
To validate these theoretical approaches, a series of flume experiments were conducted at Southern Institute of Water Resources Research (SIWRR) in Saigon - Vietnam.
Experimental set-ups
Nomenclature of tests
The physical model tests were conducted from April to August 2016 at SIWRR by Hazeme Mohamed as part of her 2nd year internship at ENTPE, proposed by Jean-Michel Tanguy (SHF) and supervised by Professor San Dinh Director of SIWRR.
The SIWRR is home to several experimental facilities for studying the behavior of waves near the coast.
We used the 40 m long, 1.2 m wide and 1.5 m maximum depth canal. It includes a wave maker that can generate regular and irregular waves, with a maximum amplitude of 0.42m, period between 0.5s and 5s. At its upstream end, the beach may be absorbent or reflective.
In order to build a database necessary for the validation of the theoretical developments, 3 types of tests were carried out:
- SmAbUn : runs in a rectangular uniform smooth bottom flume with an absorbing upstream beach
- RoAbUn : runs in a rectangular uniform partially rocky covered bottom flume with an absorbing upstream beach
- SmAbCo : runs in a rectangular flume with convergent banks and absorbing upstream beach
By varying the parameters below, it is more than 68 different tests that have been instrumented:
- Regular waves
- Constant slope along 10 m upstream of the channel: 1/25.
- Different geometries: rectangular canal or canal with linearly bank reduction.
- Variation of the bottom roughness of the channel (smooth bottom with sand and bottom covered with rocks)
- Varying conditions at the upstream boundaries: absorption or reflection.
- Variation of different wave parameters: water level, amplitude and period
In order to simplify the identification of the runs, we have established the following nomenclature:
- Upstream depth at the wave maker: D65 or D70 corresponding to depths of 65cm and 70cm
- Amplitude of the wave: A4 = 4cm (half-amplitude: the real amplitude is 8 cm counted from head to trough)
- Wave period: T4 = 4s
- Bottom surface: Sm (Smooth) or Ro (Rocks)
- Upstream boundary conditions: Re (reflection) or Ab (Absorption)
- Geometry of the section: Un (rectangular channel of constant section) or Co (rectangular channel with linear convergent section)
For example, the file D70A2T7_RoAbCo corresponds to a regular canal. Waves are generated upstream with a water height of 70cm, an amplitude of 2cm, a period of 7s on a bottom constituted in its sloping part of rocks with an absorbing beach in a convergent canal. The _D and _E suffixes are added to the file names corresponding to Data and Exploitation.
The combinations of parameters are as follows (not all combinations have been tested):
| D (cm) | A (cm) | T (s) |
|---|---|---|
| 65 | 2 | 2 |
| 70 | 4 | 4 |
| 5 | 5 | |
| 6 | ||
| 7 |
The following photos and videos illustrate the configurations:
Here are also some videos records at SIWRR of the channel in conditions close to our tests, but with boundary conditions not corresponding to our scenarios.
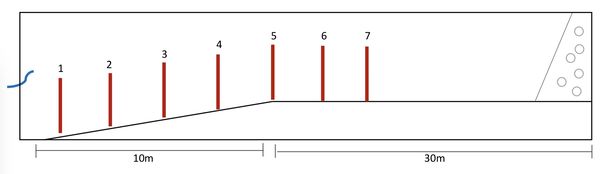
Locations of the measuring sections
The channel consists of two parts: a first part of 10 m long characterized by a slope of 1/25 which continues with an horizontal part until the boundary condition represented either by an absorbing beach (diagram below) or by a reflective wall.
The measurement sections were positioned every 2.5 m from the beginning of the slope to the section x = 10m. Sections 6 and 7 are respectively at X = 12m and X = 14m
Exploitation of measurements
We present below 4 runs which seem to us representative of the typologies of the configurations. Then we compare several similar runs by varying one parameter at a time (the period, the amplitude, the roughness, the convergence effect).
Presentation of 4 standard tests
SmAbUn
We choose test D70A4T4_SmAbUn which corresponds to the following parameters:
'Depth: 70cm, half Amplitude 4cm, Period 4s, Smooth bottom, Absorption upstream, Uniform cross sections'
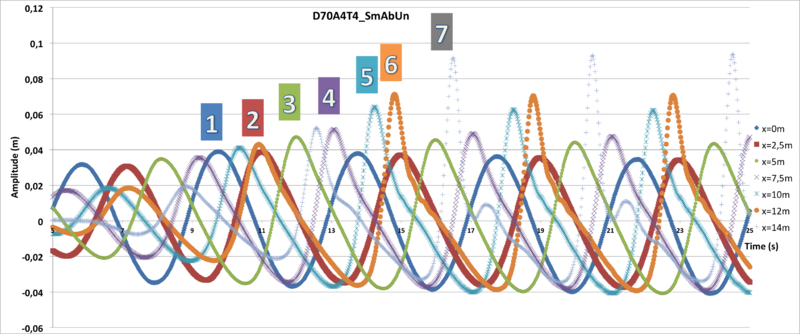
Figure 1 represents the time records of the 7 measurement devices along the channel. They are indicated with different colors. We have selected a time window that corresponds to a series of well-formed waves between the following limits: the first waves are unusable because of the movement of the wave maker and the last ones are disturbed corresponding to parasitic phenomena: transverse wave appearance and/or wave return from the not fully absorbent beach.
Thus, thanks to this diagram, we can illustrate several parameters whose longitudinal variations can be highlighted on the following graphs, but also the appearance of local disturbances.
Diagrams interpretations
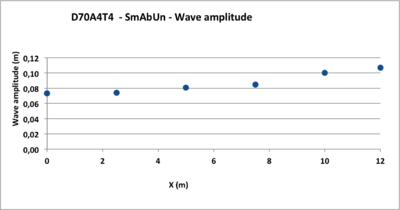
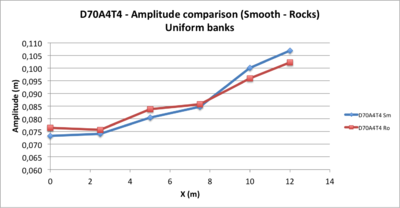
- Figure 2: In accordance with the theory, the wave amplitude increases upstream along the bottom slope
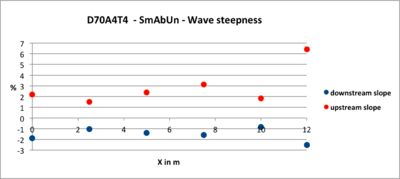
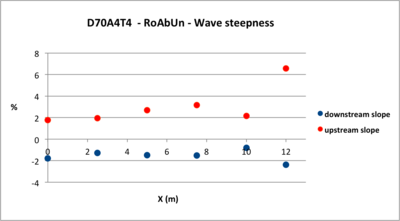
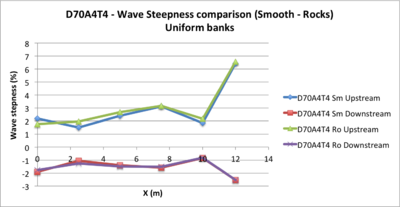
- Figure 3: Variation of the upstream and downstream slopes of the propagation waves (see Annex to see how the two slopes are calculated). The graph shows very well the stiffening of the upstream slope of the wave (in red) and the decrease of the downstream slope: this illustrates the importance of non-linear processes. We will see that they decrease with the amplitude and the period of the wave. In absolute values, the slope of the upstream stiffening is greater than that of the downstream decreasing.
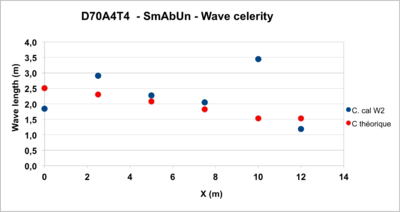
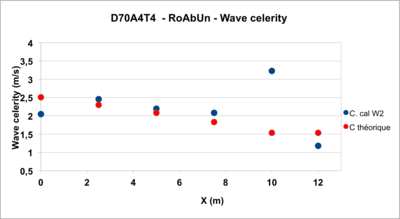
- Figure 4: the celerity of the waves decreases and remains very close to the theoretical values given by the theory of long waves. There is however a particular point located at the upstream limit of the slope (X = 10m)
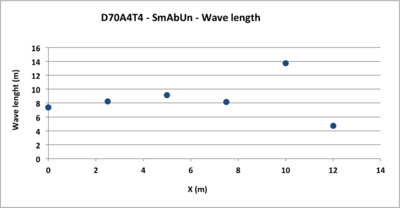
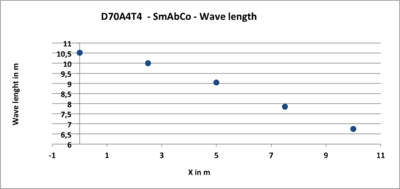
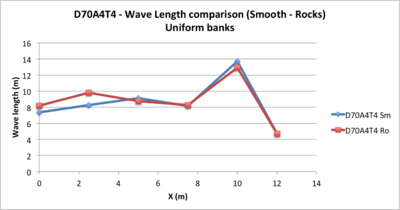
- Figure 5: The wavelength decreases along the slope. The break point of slope is also apparent.
Note : At section X = 10m, the speed is close to 1.5 m/s. Thus for a return trip of 2x20m = 40 m to return to the profile X = 14m, the wave takes 27 s. Thus the graph of Figure 1 is before the reflected wave (if any) from the absorbing range does disturb the sensors.
RoAbUn
We choose run D70A4T4_RoAbUn which corresponds to the following parameters:
'Depth: 70cm, 1/2 Amplitude 4cm, Period 4s, Rocky bottom, Absorption upstream, Uniform canal'
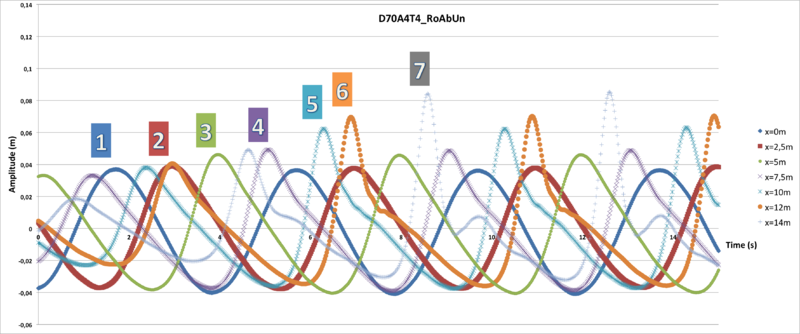
In a similar way to the other tests described above, we can illustrate several parameters whose longitudinal variations can be highlighted on the following graphs.
| - | - |
Interpretations:
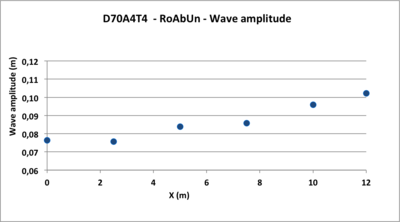
- Figure 7: According to the theory, the wave amplitude increases longitudinally along the bottom slope
- Figure 8: Variation of the upstream and downstream slopes of the propagation waves. The graph shows very well the stiffening of the upstream slope of the wave (in red) and the decrease of the downstream slope: this illustrates the importance of non-linear processes. We will see that they decrease with the amplitude and the period of the wave. In absolute values, the slope of the upstream stiffening is greater than that of the downstream decreasing.
- Figure 9: the celerity of the waves decreases and remains very close to the theoretical values given by the theory of the long waves. The same singular point is found at the upstream limit of the slope as in the previous test (X = 10m)
- Figure 10: The wavelength decreases along the slope. The upstream point of slope change is also apparent.
Note: At the right of section X = 12 m, the speed is close to 1.5 m / s. Thus for a round trip of 2x20m = 40 m to return to the profile X = 14m, the wave will put a time close to 27 s. Thus the graph of FIG. 6 is located before the reflected wave (if any) from the absorbing pad returns to disturb the sensors.
SmAbCo
We choose run D70A4T4_SmAbCo which corresponds to the following parameters :
'Depth: 70cm, 1/2 Amplitude 4cm, Period 4s, Smooth Bottom, Absorption upstream, Convergent banks'
In a similar way to the other tests described above, we can illustrate several parameters whose longitudinal variations can be illustrate on the following graphs:
Interpretations:
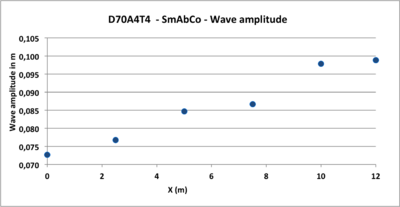
- Figure 12: According to the theory, the wave amplitude increases longitudinally along the slope of the bottom
- Figure 13: Variation of the upstream and downstream slopes of the propagation waves. The graph shows very well the stiffening of the upstream slope of the wave (in red) and the decrease of the downstream slope: this illustrates the importance of non-linear processes. We will see that they decrease with the amplitude and the period of the wave. In absolute values, the slope of the upstream stiffening is greater than that of the downstream decreasing.
- Figure 14: the celerity of the waves decreases and remains very close to the theoretical values given by the theory of the long waves. The same singular point is found at the upstream limit of the slope as in the previous test (X = 10m)
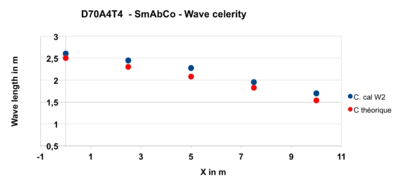
- Figure 15: The wavelength decreases along the slope. The upstream point of slope change is also apparent.
Note: At section X = 12 m, the speed is close to 1.5 m / s Thus for a return trip of 2x20m = 40 m to return to the profile X = 14m, the wave takes 27 s. Thus, the graph of Figure. 11 is located before the (eventual) reflected wave coming from the absorbing upstream boundary, which can disturb the sensors.
Comparative analysis of records
We have exploited some of the tests in a transversal manner, to identify particular behaviors of the surface waves:
- impact of the variation of the amplitude for several tests characterized by the same parameters but with roughnesses, or geometries either uniform, or linear
- impact of the change in the period
- impact of the variation of the initial amplitude
- comparison for the same test carried out in uniform or converging section
- impact of roughness variation
Impact of the variation of the amplitude for several tests with the same parameters
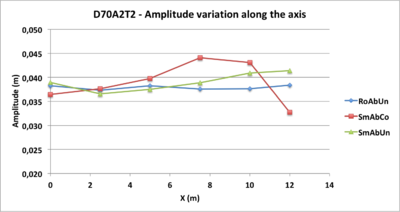
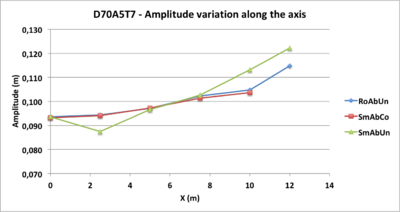
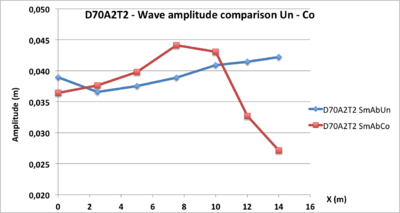
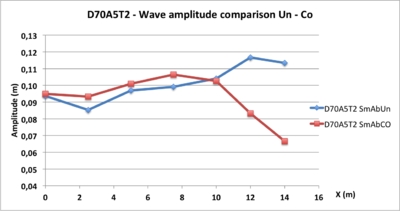
We have compared several tests characterized by D70, by Ab absorbing boundary conditions and for the same period T5. These are tests D70A5T5, D70A2T2 and D70A5T7 in RoAbUn, SmAbCo and SmAbUn conditions
- Figure 16: amplitudes variations for the 3 runs are increasing according to the slope, which is in accordance with the theory.
- Figure 17: the initial amplitudes of the waves generated by the wave maker are not always well respected: all the curves of the same diagram should start from the same point to X = 0
- Figure 18: there is a sharp change in amplitude at the arrival at the top of the slope.
Impact of period variation on wave propagation conditions
We chose the configuration of rectangular channel D70A4 with convergent banks (SmAbCo) and compare tests realized with different periods (T2, T4, T5 and T6)
Comments
- Figure 19: the amplitude increases along the slope, except for the lowest period (T2) which decreases at the top of the slope. The curves T4 and T5 are quite similar. The curve T6 is lower because it does not start from the same origin
- Figure 20: The slopes of low frequency waves are very close in absolute value and evolve little, which shows the quasi-linear nature of the propagation. For larger frequencies, upstream stiffening are larger in absolute value than downstream decreasing, which is maintained at a value close to 1% while the stiffening increases gradually along the slope
- Figure 21: all waves of the same amplitude propagate upstream with a decreasing speed close to -0.1 m / s / ml, which can be written as: $ dC / dX = -0.1 $ . After the point-break of slope, the celerity tends to take a constant value close to 1.6 m / s
- Figure 22: the wavelength decreases upstream with intensity varying with amplitude.
From previous figures, we can deduce the following empirical relationships: knowing that L = CT, the law of variation of the wavelength dL / dX = dC / dx * T = -0.1 * T, which can be checked on the figure 22
Impact of amplitude variation on wave propagation
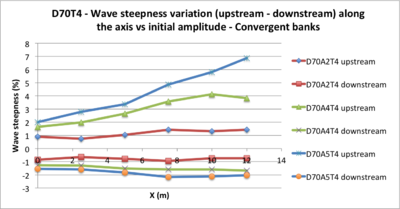
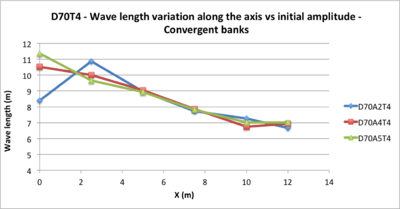
In order to highlight the impact of the amplitude variation on the wave propagation conditions, we chose to compare several tests corresponding to D70T4 but with different amplitudes: A2, A4 and A5 in the SmAbCo configuration ( smooth bottom, absorbent upstream boundary and convergent banks)
Comments
- Figure 23: The amplitude increases along the axis proportionally to the value of the initial amplitude. For the lowest initial amplitude, the wave does not "increase": the amplitude remains constant along the slope, which confirms the quasi-linear nature of the test
- Figure 24: the slopes of the upstream curves of stiffening are more important than the downstream curves of subsidence
- Figure 25: The wave speed tends to decrease uniformly regardless of the initial amplitude
- Figure 26: the wavelength tends to decrease uniformly regardless of the initial amplitude with a slope close to 30%
From previous schemes, we can deduce the following 2 empirical relationships: L=-0,3*X+10,5 et C=-1/12*X+2,6
Demonstration of the convergence effect of the banks with respect to the uniform canal
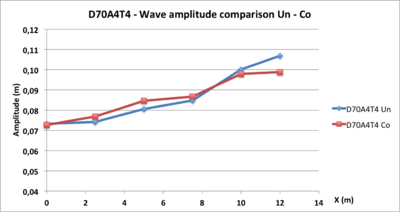
We chose to compare 2 runs D70A4T4: SmAbUn and SmAbCo
Comments
- the differences between the curves Un and Co appear on each graph from the top of the slope (X = 10m)
- for low periods (Figures 26, 27, 28 and 31) there is a sharp drop in amplitude below the starting amplitude at the wave maker (X = 0m)
- the smaller the period is (Figures 28, 29, 30), the lower the curve Co decreases
Impact of bottom roughness on wave propagation conditions
We chose 2 D70A4T4 runs and compare the SmAbUn and RoAbUn configurations
Comments
- Figure 32: the change of amplitudes is not very important in intensity. However, a greater roughness causes a damping of the wave amplitude
- Figure 33: There are few modifications concerning the stiffening and the decreasing of the waves
- Figure 34: few differences in celerity decreasing along the slope, with however the presence in both cases of a peak celerity at the high point of the slope failure
- Figure 35: few differences for the wavelength that decreases along the slope, with however the presence in both cases of a long wave peak at the high point of the slope failure
Appearance of a particular point in X = 10m
In the curves above, there is a discontinuity at the upstream point of slope failure. Several hypotheses can be advanced: either the sensor did not work well, or it was implanted in the wrong place or there is a particular phenomenon at this point.
Note that all the runs carried out in uniform channel (SmAbUn and RoSmUn) present this point whereas the tests carried out in convergent channel (SmAbCo) do not show it.
Annex
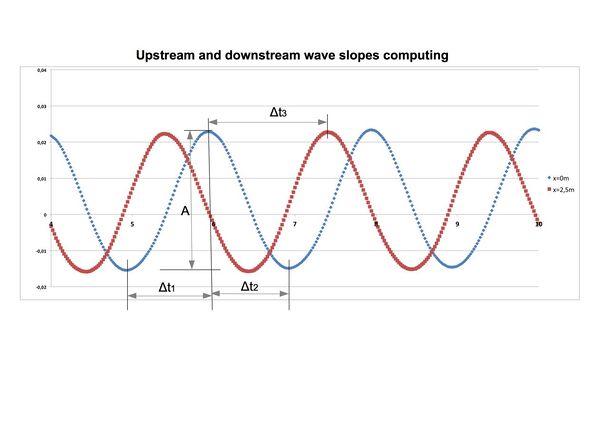 |
|
Conclusion
Test results
The tests conducted at SIWRR are interesting in several ways:
- They make possible to highlight the behavior of long waves as they progress in an estuary of rectangular shape, whose bottom is characterized by a regular slope ascending upstream (example: estuary of the Gironde). Two geometries of variation of sections were studied: uniform on the whole channel on the one hand and convergent upstream on the other hand.
- they made it possible to build a database freely available on the internet
- Compared to theories, they allowed to verify the following points:
- * the wave amplitude increases upstream because of the slope of the rising bottom and also increased by the restriction of sections with convergent banks in these cases
- * the curve of the waves remains fairly homogeneous in the case of small amplitudes and weak periods, which shows that the progression is quasi-linear. But the greater the amplitudes or the period is large, the waves stiffen on their upstream face and collapse on their downstream face.
- * wavelengths decrease upstream
- * the particular behavior of the wave deformations at the point of upstream slope failure (X = 10 m) is not explicable.
Recommendations to modellers
Given the choice of parameters in all of these tests, modelers are recommended to test several types of models:
- the most interesting configurations in the sense of the richness of the data produced are D70AiTj (i = 2,4,5 and j = 2,4,5,6)
- it is likely that the steep slope makes the Saint-Venant models difficult to use, but it is worthwhile to test them
- linearized models can be used for low amplitudes and low periods
- non-linearities must be characterized by disconnecting each non-linear term: celerity or friction, to highlight their respective impacts
- It is recommended to reproduce amplitude and period sensitivity curves (tests D70AiTj)
- It is also necessary to finely analyze what happens at the point of upstream slope failure (between the slope and the horizontal at the abscissa X = 10m). Some tests have shown particularities of wave propagation at this point, that must be examined
- the comparison of numerical modeling model results with the linear analytical solution in the case of uniform canal and convergent banks canal is quite relevant in quasi linear configurations (weak period, weak amplitude)
Authors and acknowledgments
- Hazeme Mohamed: tests conducted at SIWRR in Saigon, Vietnam
- Jean-Michel Tanguy: exploitation of the essays and writing of this page
We thank Prof. San Dinh, director of the Southern Institute of Water Resources Research in Saigon, Vietnam, for allowing the completion of these trials, the mentoring of the trainee. These tests were made possible thanks to the financing of ENTPE as part of the FORM @ HYDRO project. We would like to thank in particular Bernard Clément, Director of the City & Environment Department, HDR Teacher-Researcher at LEHNA-IPE, ENTPE
 S'abonner à un flux RSS
S'abonner à un flux RSS