C.07 - Apprentissage : analyse a posteriori des erreurs de prévision

Principe

La comparaison d'un ensemble de sorties passés d'un système de prévision (déterministe) aux observations correspondantes peut apporter beaucoup d'information sur l'incertitude de prévision. En se basant sur un ensemble de prévisions passées considéré comme représentatif (par exemple une chronique de prévision), il est en effet possible de décrire statistiquement les erreurs de prévision faites (également appelées résidus), voire de chercher à modéliser ces erreurs à travers une corrélation avec un facteur explicatif.

Approches descriptives pures

L'approche la plus simple : construire une statistique sur les prévisions passées

La première approche possible consiste à simplement calculer des statistiques sur l'ensemble des erreurs disponibles :

• moments statistiques : moyenne, écart-type...
• quantiles statistiques (fiche A.09).

En supposant le système modélisé (bassin versant, réseau hydrographique...) et l'outil de prévision stationnaires, on peut estimer l'incertitude des prévisions à venir en se basant sur ces statistiques calculées.

Exemple 1. Le SPC Orge – Yvette a mis en service un modèle de prévision hydraulique en 2010. Depuis, le modèle a été employé trente-huit fois pour effectuer des prévisions sur des crues d'amplitude moyenne à la station d'Athis-Mons. Le SPC a enregistré l'ensemble de ses prévisions et dispose donc d'une quarantaine de résidus. Il peut donc estimer les quantiles statistiques q10(ε) et q90(ε) de ces résidus : q10(ε) = -1,0 m3/s et q90(ε) = +2,3 m3/s. Pour ses prochaines prévisions, le SPC Orge – Yvette accompagnera la valeur fournie par le modèle, Q , d'un intervalle de prévision à 80 % : .

Construire une statistique par classe d'une variable explicative

Si on suppose que l'incertitude de prévision est (plus ou moins) corrélée avec une ou plusieurs variables considérées comme explicatives, il est possible d'étendre la démarche précédente en définissant des sous-groupes au sein de l'ensemble des données possibles, correspondants à des classes de la (ou des) variables explicative(s). Les statistiques sont ensuite calculées pour chaque classe.

Pour que cette approche soit utilisable en temps réel, il est nécessaire que la ou les variables explicatives soient disponibles lors de l'élaboration de la prévision (ne dépendant donc pas d'observations à venir). Il suffit alors de choisir la statistique à prendre en compte en fonction de la classe à laquelle appartiennent la ou les variables explicatives. Ainsi, la hauteur Ht ou le débit Qt observé à l'instant de prévision sont utilisables dans ce but, de même que la prévision de hauteur ou de débit à venir mais pas la hauteur ou le débit à venir !

Le nombre de classes doit être choisi en fonction du nombre de prévisions passées disponibles pour que chaque classe en comporte un nombre suffisant, permettant d'établir une estimation significative des statistiques. Aussi, l'échantillon doit être d'autant plus fourni que le nombre de variables explicatives sélectionnées est élevé.

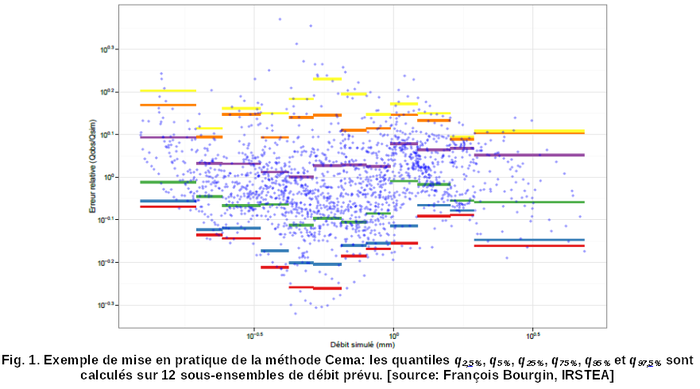
Exemple 2. La méthode CEMA, développée par l'IRSTEA, consiste à estimer, sur une série d'erreurs passées, un petit nombre de quantiles empiriques de l'erreur de prévision d'un modèle déterministe pour différentes gammes du débit prévu. Cette connaissance permet ensuite de fournir une estimation des intervalles de prévision en fonction du débit prévu par le modèle déterministe. En pratique, la série des erreurs passées disponibles est scindée en 12 sous-ensembles correspondant à des gammes croissantes du débit prévu. Les quantiles des erreurs de prévision correspondant aux intervalles de prévision recherchés (par exemple q5 % et q95 % pour l'intervalle de prévision à 90 %) sont calculés pour chaque sous-ensemble (Fig. 1). En mode prévision, l'intervalle prédictif est alors calculé en prenant les valeurs des quantiles du sous-ensemble correspondant à la valeur du débit prévu par le modèle.

Limites de l'approche descriptive pure

Ces approches supposent que le système de prévision et l'outil de prévision sont stationnaires, de façon à ce que les informations calculées sur des prévisions passées s'appliquent aux prévisions futures.

Par ailleurs, ces descriptions statistiques sont valables sur la gamme d'erreur qui a pu être analysée, c'est-à-dire qui est représentée dans l'échantillon étudié. De même, l'analyse par classes d'une ou plusieurs variables explicatives n'est utilisable que si la valeur de cette (ces) variable(s) explicative(s) pour la prévision à venir appartient à la gamme des valeurs sur l'échantillon initial. Au-delà, il s'agit d'une extrapolation sur laquelle nous n'avons pas de contrôle.

Pour tester la robustesse de ces approches, il peut être pertinent d'adopter une approche en calage / contrôle, c'est-à-dire de scinder l'échantillon en deux sous-ensembles, de réaliser les calculs sur chaque sous-ensemble séparément et de comparer les résultats sur l'autre sous-ensemble.

Introduire des hypothèses supplémentaires : apporter un modèle d'erreur

Choisir un modèle d'erreur

Les échantillons de prévisions passées peuvent être assez restreints et n'apporter qu'une information très limitée. Il est possible de l'enrichir en ajoutant une ou plusieurs hypothèses supplémentaires, c'est-à-dire en construisant un modèle de l'erreur.

Ces modèles peuvent être ou non fonction de variables explicatives (exemples 3 et 4).

Ces modèles peuvent être ou non paramétrés. Les paramètres des modèles d'erreur sont parfois appelés hyper-paramètres pour les distinguer de ceux du modèle hydrologique ou hydraulique. Il est nécessaire d'estimer ces paramètres, soit par calage (séparé de ou simultané avec le calage des paramètres du modèle hydraulique ou hydrologique), soit par analyse statistique de l'échantillon des erreurs de prévision passées.

Exemple 3. Dans la section 2.1, nous avons proposé d'analyser un ensemble de prévisions passées pour déterminer les statistiques basiques des erreurs de prévision sur cet échantillon : la moyenne, l'écart-type et les quantiles d'erreur. Cependant, il n'est pas possible d'estimer tous les quantiles rares : il est, par exemple, impossible d'estimer ainsi le quantile q5 % si l'échantillon ne compte que 10 prévisions. Si en revanche on suppose un modèle de l'erreur, il est possible d'aller chercher ces quantiles rares. Ainsi, en supposant que les erreurs sont issues d'une distribution gaussienne dont la moyenne et l'écart-type sont égaux à la moyenne et à l'écart-type statistiques calculés sur l'échantillon (analyse statistique pour déterminer les paramètres du modèle d'erreur), n'importe quel quantile est théoriquement calculable. Toutefois, il faut se poser la question de la signification de ces quantiles rares calculés sur très peu de données : leur validité repose fortement sur celle du modèle d'erreur (i. e., des hypothèses introduites).

Un des intérêts d'ajouter des hypothèses sur la distribution des erreurs est de rendre (formellement) possible une extrapolation (exemple 4). Cependant, ces hypothèses ne peuvent être validées que sur l'échantillon de données disponibles et deviennent d'autant moins vérifiées qu'on s'éloigne de la gamme de valeurs explorée dans cet échantillon : les extrapolations sur des valeurs éloignées de cette gamme sont donc hasardeuses ; là encore, on s'appuie fortement sur le modèle d'erreur.

Ici encore, une approche en calage / contrôle permet de contrôler la pertinence du modèle d'erreur choisi.

Recherche d'une relation entre l'erreur et la variable explicative

La section 2.2 proposait de décrire les erreurs passées en calculant leurs statistiques pour des classes d'une variable explicative. On peut étendre la démarche en construisant un modèle d'erreur qui prenne explicitement en compte cette (ou ces) variable(s) explicative(s).

Ces modèles prennent souvent la forme de régressions donnant les descripteurs de l'erreur (typiquement la moyenne et l'écart-type) en fonction de la ou des variable(s) explicative(s).

Un intérêt de cette approche est de faciliter l'extrapolation tant que l'information apportée par le modèle reste valable.

Exemple 4. L'incertitude de prévision de certains modèles hydrauliques est parfois donnée « par dires d'expert » : l'incertitude est par exemple de ± 20 cm. Cependant, on sait que l'incertitude est beaucoup plus important lors des très fortes crues, quand le modèle fonctionne en extrapolation. Il peut donc être pertinent de construire un modèle d'erreur de l'incertitude en fonction du débit estimé. Ce modèle pourra être une loi normale de moyenne nulle (absence de biais) et d'écart-type, fonction du débit estimé.

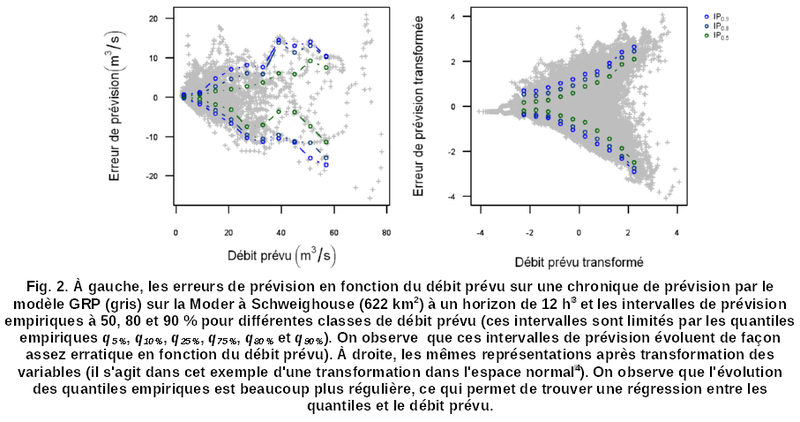
La méthode de la régression de quantiles

La régression de quantiles est une extension des approches précédentes dont le but est de fournir une relation empirique entre un quantile qy de l'incertitude (pour différentes valeurs de y) et la variable prévue X (de façon déterministe par l'outil de prévision). X sera pour nous le débit ou la hauteur.

Une fois la fonction fy et la régression spécifiées pour différentes valeurs de y (par exemple les paramètres ay et by), on peut directement estimer les intervalles de prévision en fonction de la prévision déterministe de l'outil de prévision .

En effet, la régression permet de déterminer les valeurs transformées des différents quantiles recherchés à partir de la valeur prévue x et les valeurs des quantiles sont déterminées en appliquant une transformation inverse .

Cette méthode, décrite par Weerts et al. (2011) a été testée sur de nombreux bassins et s'est révélée raisonnablement fiable sur un grand nombre. Par ailleurs, comme une relation a été définie entre les quantiles prévus (et donc les intervalles de prévision) et la variable prévue, la méthode peut être facilement utilisée en extrapolation, sur des crues d'une intensité non explorée au calage en utilisant la relation précédente). L'emploi en extrapolation est cependant hasardeux dès qu'on s'éloigne significativement de l'intervalle d'intensité des crues exploré au calage.

Points sensibles

Quand un modèle d'erreur est introduit, il est important que sa validité soit questionnée. En particulier, il est nécessaire que soit spécifiée la gamme (minimale) de validité des hypothèses (par exemple, pour une prévision de hauteur comprise entre Hmin et Hmax, ou pour une valeur de variable explicative X comprise entre Xmin et Xmax)

La robustesse de ces méthodes dépend fortement de la richesse (informative) de l'échantillon de données (couples d'observations et de prévisions correspondantes). Rejouer des prévisions sur des séries temporelles ou des crues passées peut fournir suffisamment de données pour caler ce type de méthodes. La robustesse doit par ailleurs être contrôlée ; une approche en calage / contrôle (en scindant l'ensemble des données en deux sous-groupes qui servent alternativement à caler puis à contrôler la méthode) est appropriée. Ce contrôle indépendant permet notamment de tester le fonctionnement en extrapolation.

Ces méthodes se fondent sur une hypothèse importante de stationnarité : les données doivent avoir été collectées sur une période suffisamment courte et proche du présent pour que les conditions d'écoulement et de prévisions puissent être estimées stationnaires.

Voir également

Fiche A.09 – Quantiles et médiane

Pour aller plus loin

Weerts et al. (2011). Estimation of predictive hydrological uncertainty using quantile regression: Examples from the National Flood Forecasting System (England and Wales). Hydrol. Earth Syst. Sci., 15, 255–265, doi:10.5194/hess-15-255-2011. [disponible sur http://www.hydrol-earth-syst-sci.net/15/255/2011/hess-15-255-2011.pdf]

---