Green et Ampt (modèle de) (HU) : Différence entre versions
(→Formulation mathématique) |
|||
| Ligne 18 : | Ligne 18 : | ||
Le modèle de Green et Ampt s'écrit de la façon suivante par unité de surface infiltrante : | Le modèle de Green et Ampt s'écrit de la façon suivante par unité de surface infiltrante : | ||
| − | <center><math>f(t) = K.\left[\frac{Ψ.(θ_s-θ_i}{F(t)}+1\right] \qquad(1)</math></center> | + | <center><math>f(t) = K.\left[\frac{Ψ.(θ_s-θ_i)}{F(t)}+1\right] \qquad(1)</math></center> |
Avec : | Avec : | ||
| Ligne 26 : | Ligne 26 : | ||
* <math>θ_s</math> : taux d'humidité du sol saturé (m/m) ; | * <math>θ_s</math> : taux d'humidité du sol saturé (m/m) ; | ||
* <math>θ_i</math> : taux initial d'humidité (m/m) ; | * <math>θ_i</math> : taux initial d'humidité (m/m) ; | ||
| − | * <math>F(t)</math> : | + | * <math>F(t)</math> : hauteur d'eau infiltrée (m). |
<center><math>F(t) = \int_0^t f(τ).dτ \qquad(2)</math></center> | <center><math>F(t) = \int_0^t f(τ).dτ \qquad(2)</math></center> | ||
| + | ==Intérêt et limite du modèle== | ||
| + | |||
| + | Ce modèle de type [[Horton (modèle de) (HU)|hortonien]] correspond à une saturation progressive du sol. Il est simple et fournit des résultats corrects pour des sols relativement grossiers (sableux ou argilo-sableux). Il peut être utilisé pour représenter les pertes continues mais également pour représenter l'infiltration dans les ouvrages d'infiltration. | ||
<u>Bibliographie</u> | <u>Bibliographie</u> | ||
* Green, W.H., Ampt, G. (1911) : Studies of soil physics, part I – the flow of air and water through soils. J. Ag. Sci. 4 ; p.1-24 | * Green, W.H., Ampt, G. (1911) : Studies of soil physics, part I – the flow of air and water through soils. J. Ag. Sci. 4 ; p.1-24 | ||
Version du 29 avril 2022 à 15:19
Traduction anglaise : Green et Ampt model
Dernière mise à jour : 29/04/2022
Modèle de représentation de l'infiltration dans les sols (Green et Ampt, 1911).
Principes du modèle
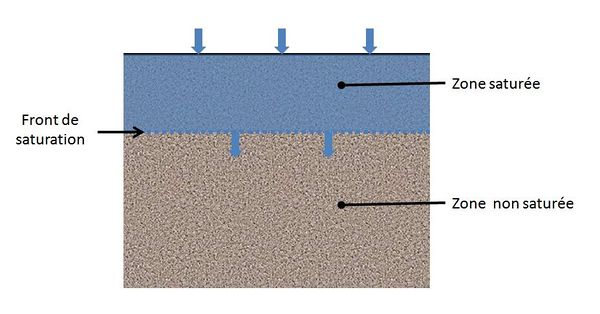
Le principe de base du modèle est la progression d'un front de saturation homogène dans le sol (figure 1).
L'eau qui s'infiltre progresse vers le bas sous le double effet des forces de pesanteur et des forces de succion ; le front de saturation est supposée horizontal. L'équation de conservation permet de déterminer à chaque instant l'équilibre entre le volume d'eau stocké dans la zone saturée en fonction de l'extension de cette zone et le débit infiltré. Le sol est supposé homogène (porosité et perméabilité intrinsèque constante). Le modèle nécessite également que le phénomène s'arrête avant que l'eau d'infiltration n'est atteint une zone non saturée plus profonde.
Formulation mathématique
Le modèle de Green et Ampt s'écrit de la façon suivante par unité de surface infiltrante :
Avec :
- $ f(t) $ : taux d'infiltration à l'instant t (m/s) ;
- $ K $ : conductivité hydraulique du sol (supposée constante) (m/s) ;
- $ Ψ $ : succion (supposée constante) (m) ;
- $ θ_s $ : taux d'humidité du sol saturé (m/m) ;
- $ θ_i $ : taux initial d'humidité (m/m) ;
- $ F(t) $ : hauteur d'eau infiltrée (m).
Intérêt et limite du modèle
Ce modèle de type hortonien correspond à une saturation progressive du sol. Il est simple et fournit des résultats corrects pour des sols relativement grossiers (sableux ou argilo-sableux). Il peut être utilisé pour représenter les pertes continues mais également pour représenter l'infiltration dans les ouvrages d'infiltration.
Bibliographie
- Green, W.H., Ampt, G. (1911) : Studies of soil physics, part I – the flow of air and water through soils. J. Ag. Sci. 4 ; p.1-24
 S'abonner à un flux RSS
S'abonner à un flux RSS