Pluie de projet simple triangle (HU) : Différence entre versions
(→Mode de construction et domaine d'utilisation) |
|||
| (Une révision intermédiaire par un utilisateur est masquée) | |||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : simpletriangle design storm'' | ''<u>Traduction anglaise</u> : simpletriangle design storm'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 27/09/2022 |
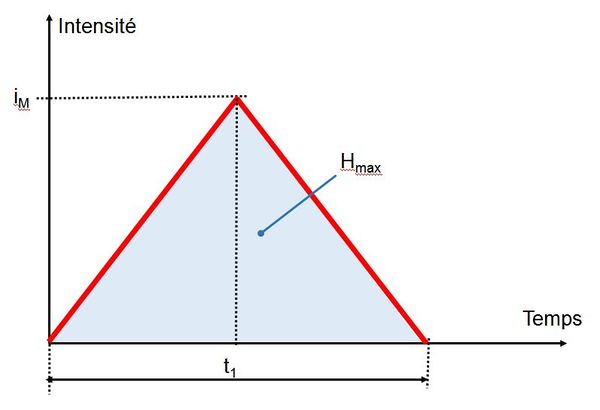
| − | + | Forme simplifiée de [[Pluie de projet (HU)|pluie de projet]] dérivée des [[Pluie de projet double triangle (HU)|pluies de projet double triangle]] ; le plus simple consiste à prendre une forme triangulaire symétrique (triangle isocèle, voir ''figure 1''). | |
| − | Forme simplifiée de [[Pluie de projet (HU)|pluie de projet]] dérivée des [[Pluie de projet double triangle (HU)|pluies de projet double triangle]] (''figure 1''). | + | |
==Mode de construction et domaine d'utilisation== | ==Mode de construction et domaine d'utilisation== | ||
| − | [[File: | + | [[File:pluie_projet_simple_triangle1.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Pluie de projet simple triangle.''</center>]] |
| − | La durée de la pluie <math>t_1</math> peut être prise égale à <math>2.K</math> (Chocat ''et al.'', 1981), K étant le [[Lag time (HU)|lag time]] du bassin versant étudié. | + | La durée de la pluie <math>t_1</math> peut être prise égale à <math>2.K</math> (Chocat ''et al.'', 1981), <math>K</math> étant le [[Lag time (HU)|lag time]] du bassin versant étudié. |
La hauteur totale de pluie, <math>H_{max}</math>, précipitée peut se calculer en utilisant les coefficients <math>a</math> et <math>b</math> d'un [[Montana (formule type) (HU)|ajustement de type Montana]] de la pluviométrie locale : | La hauteur totale de pluie, <math>H_{max}</math>, précipitée peut se calculer en utilisant les coefficients <math>a</math> et <math>b</math> d'un [[Montana (formule type) (HU)|ajustement de type Montana]] de la pluviométrie locale : | ||
| Ligne 19 : | Ligne 18 : | ||
| − | Il est alors possible de calculer simplement <math> | + | Il est alors possible de calculer simplement <math>i_M</math> : |
| − | + | ||
| − | |||
| + | <center><math>i_M=\frac{2.H_{max}}{t_1}</math></center> | ||
| + | Ce modèle est bien adapté pour des bassins versants de petite taille (lag time inférieur à 10 minutes). Pour des bassins versants plus grands il est préférable d'utiliser des [[Pluie de projet double triangle (HU)|pluies de projet double triangle]]. | ||
<u>Bibliographie</u> | <u>Bibliographie</u> | ||
* Chocat, B., Thibault, S., Bouyat, M. (1981) : Étude comparative des résultats fournis par la méthode de Caquot et le modèle du réservoir linéaire ; TSM l'eau ; n°7 ; pp 417-424. | * Chocat, B., Thibault, S., Bouyat, M. (1981) : Étude comparative des résultats fournis par la méthode de Caquot et le modèle du réservoir linéaire ; TSM l'eau ; n°7 ; pp 417-424. | ||
Version actuelle en date du 27 septembre 2022 à 12:04
Traduction anglaise : simpletriangle design storm
Dernière mise à jour : 27/09/2022
Forme simplifiée de pluie de projet dérivée des pluies de projet double triangle ; le plus simple consiste à prendre une forme triangulaire symétrique (triangle isocèle, voir figure 1).
[modifier] Mode de construction et domaine d'utilisation
La durée de la pluie $ t_1 $ peut être prise égale à $ 2.K $ (Chocat et al., 1981), $ K $ étant le lag time du bassin versant étudié.
La hauteur totale de pluie, $ H_{max} $, précipitée peut se calculer en utilisant les coefficients $ a $ et $ b $ d'un ajustement de type Montana de la pluviométrie locale :
Il est alors possible de calculer simplement $ i_M $ :
Ce modèle est bien adapté pour des bassins versants de petite taille (lag time inférieur à 10 minutes). Pour des bassins versants plus grands il est préférable d'utiliser des pluies de projet double triangle.
Bibliographie
- Chocat, B., Thibault, S., Bouyat, M. (1981) : Étude comparative des résultats fournis par la méthode de Caquot et le modèle du réservoir linéaire ; TSM l'eau ; n°7 ; pp 417-424.
 S'abonner à un flux RSS
S'abonner à un flux RSS