SCS (modèle) (HU) : Différence entre versions
| (11 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : SCS model'' | ''<u>Traduction anglaise</u> : SCS model'' | ||
| − | Modèle empirique non linéaire de transformation pluie-débit applicable sur les bassins versants ruraux ou peu urbanisés. L'acronyme SCS vient de ''Soil conservation service'', organisme américain qui a initialement conçu ce modèle. | + | <u>Dernière mise à jour</u> : 17/11/2022 |
| + | |||
| + | Modèle empirique non linéaire de transformation pluie-débit applicable sur les bassins versants ruraux ou peu urbanisés ; ce modèle a été adapté en France sous le nom de méthode [[Socose (méthode) (HU)|SOCOSE]]. | ||
| + | |||
| + | <u>Nota</u> : L'acronyme SCS vient de ''Soil conservation service'', organisme américain qui a initialement conçu ce modèle. | ||
== Formulation du modèle == | == Formulation du modèle == | ||
On note : | On note : | ||
| + | * <math>R</math> : volume ruisselé (correspond au cumul de [[Pluie nette (HU)|pluie nette]]) (mm) ; | ||
| + | * <math>P</math> : hauteur de précipitation (correspond au cumul de [[Pluie brute (HU)|pluie brute]]) (mm) ; | ||
| + | * <math>S</math> : [[Capacité d’infiltration (HU)|capacité d'infiltration potentielle maximale]] du sol (mm) ; | ||
| + | * <math>I_a</math> : [[Perte initiale (HU)|pertes initiales]] (correspondent dans ce cas à l'interception par la végétation et au stockage dans les dépressions du sol, mais également à la saturation du sol de surface) (mm) ; | ||
| + | * <math>CN</math> : [[Coefficient d’aptitude au ruissellement / CN (HU)|coefficient d'aptitude au ruissellement]] (paramètre adimensionnel compris entre 30 et 100). | ||
| − | + | On écrit : | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | <center><math>R = \frac{(P- | + | <center><math>R = \frac{(P-I_a)^2}{P-I_a + S} \quad (1)</math></center> |
| + | |||
<u>Remarques</u> : | <u>Remarques</u> : | ||
| − | + | * <math>R</math> est nul tant que <math>P < I_a</math> ; | |
| − | * <math>R</math> est nul tant que <math>P < | + | * La relation entre <math>R</math> et <math>P</math> tend asymptotiquement vers la droite d'équation <math>R = P – I_a – S</math> lorsque <math>P</math> devient grand. |
| − | * La relation entre <math>R</math> et <math>P</math> tend asymptotiquement vers la droite d'équation <math>R = P – | + | |
On écrit également : | On écrit également : | ||
| − | <center><math>S = 25.4\frac{ | + | |
| + | <center><math>S = 25.4\frac{1000}{CN-10} \quad (2)</math></center> | ||
| + | |||
et | et | ||
| − | <center><math> | + | |
| + | <center><math>I_a = 0,2.S \quad (3)</math></center> | ||
| + | |||
Finalement, la fonction de production se formule ainsi : | Finalement, la fonction de production se formule ainsi : | ||
| − | |||
| − | <center><math>S = 25.4\frac{ | + | <center><math>R = \frac{(P - 0,2.S)^2}{P + 0,8.S} \quad (4)</math></center> |
| + | |||
| + | |||
| + | et: | ||
| + | |||
| + | |||
| + | <center><math>S = 25.4\frac{1000}{CN-10} \quad (5)</math></center> | ||
| + | |||
| − | |||
| − | |||
| − | |||
== Choix des paramètres == | == Choix des paramètres == | ||
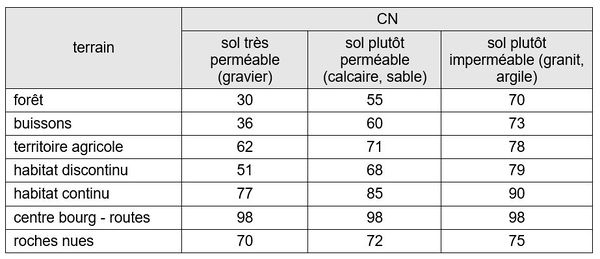
| − | En l’absence de mesures locales, les valeurs de <math>CN</math> peuvent être choisies dans le tableau | + | En l’absence de mesures locales, les valeurs de <math>CN</math> peuvent être choisies dans le tableau de la ''figure 1'' : |
| + | |||
| + | |||
| + | [[File:valeurs CN.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Ordre de grandeur de <math>CN</math> en fonction de la perméabilité du sol et de son occupation.''</center>]] | ||
| − | + | ==Intérêt du modèle== | |
| + | Ce modèle est difficile à utiliser d'une part à cause de son caractère non linéaire, d'autre part parce qu'il est très sensible au choix de <math>CN</math>, lequel dépend de multiples paramètres : nature du sol, type de culture, pluviométrie, saison, etc. | ||
| − | + | En l'absence de mesures, il est prudent de tester différentes valeurs de <math>CN</math> pour évaluer l'incertitude sur le résultat. | |
[[Catégorie:Dictionnaire_DEHUA]] | [[Catégorie:Dictionnaire_DEHUA]] | ||
| + | [[Catégorie:Modélisation_de_la_transformation_pluie-débit_(HU)]] | ||
Version actuelle en date du 17 novembre 2022 à 18:11
Traduction anglaise : SCS model
Dernière mise à jour : 17/11/2022
Modèle empirique non linéaire de transformation pluie-débit applicable sur les bassins versants ruraux ou peu urbanisés ; ce modèle a été adapté en France sous le nom de méthode SOCOSE.
Nota : L'acronyme SCS vient de Soil conservation service, organisme américain qui a initialement conçu ce modèle.
[modifier] Formulation du modèle
On note :
- $ R $ : volume ruisselé (correspond au cumul de pluie nette) (mm) ;
- $ P $ : hauteur de précipitation (correspond au cumul de pluie brute) (mm) ;
- $ S $ : capacité d'infiltration potentielle maximale du sol (mm) ;
- $ I_a $ : pertes initiales (correspondent dans ce cas à l'interception par la végétation et au stockage dans les dépressions du sol, mais également à la saturation du sol de surface) (mm) ;
- $ CN $ : coefficient d'aptitude au ruissellement (paramètre adimensionnel compris entre 30 et 100).
On écrit :
Remarques :
- $ R $ est nul tant que $ P < I_a $ ;
- La relation entre $ R $ et $ P $ tend asymptotiquement vers la droite d'équation $ R = P – I_a – S $ lorsque $ P $ devient grand.
On écrit également :
et
Finalement, la fonction de production se formule ainsi :
et:
[modifier] Choix des paramètres
En l’absence de mesures locales, les valeurs de $ CN $ peuvent être choisies dans le tableau de la figure 1 :
[modifier] Intérêt du modèle
Ce modèle est difficile à utiliser d'une part à cause de son caractère non linéaire, d'autre part parce qu'il est très sensible au choix de $ CN $, lequel dépend de multiples paramètres : nature du sol, type de culture, pluviométrie, saison, etc.
En l'absence de mesures, il est prudent de tester différentes valeurs de $ CN $ pour évaluer l'incertitude sur le résultat.
 S'abonner à un flux RSS
S'abonner à un flux RSS