Normand (modèle de) (HU) : Différence entre versions
(discuter) |
|||
| (11 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Normand's model'' | ''<u>Traduction anglaise</u> : Normand's model'' | ||
| − | + | <u>Dernière mise à jour</u> : 03/03/2025 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | Mode de construction de [[Pluie de projet (HU)|pluies de projet]], dérivé du [[Chicago (pluie de projet type) (HU)|modèle de Chicago]], tenant compte du fait que la [[Période de retour (HU)|période de retour]] d'une pluie n'est pas la même pour toutes les durées d'analyse. | ||
| + | ==Principes du modèle== | ||
| − | + | Le modèle de Normand a été établi à partir d'une analyse des [[Intensité moyenne maximale (HU)|intensités moyennes maximales]] calculées sur des pluies observées (Normand & Veyrat, 1976). Cette analyse a permis de déterminer les périodes de retour (inférieures à 10 ans) qu'il fallait prendre en compte pour des durées, <math>t_2</math>, inférieures ou supérieures à la durée, <math>t_1</math>, pour laquelle on avait choisi une période de retour décennale. Les conclusions sont synthétisées dans l'abaque de la ''figure 1''. | |
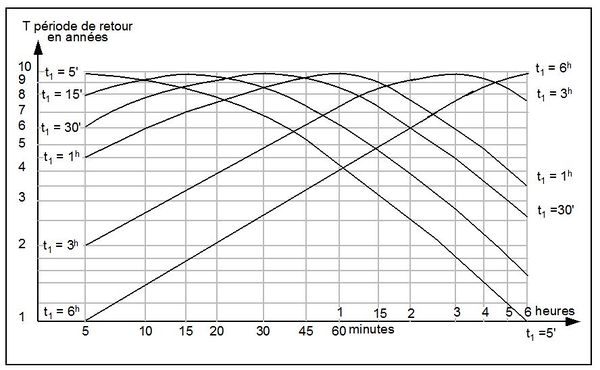
| + | [[File:Normand.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Période de retour des intensités <math>I(t_2)</math> associées à une intensité décennale <math>I(t_1)</math> dans un hyétogramme décennal centré sur I(t1). Valeurs moyennes françaises d'après Normand ; <u>Source</u> : Deutsch ''et al.'', 1989].''</center>]] | ||
| − | + | ==Intérêt et limite du modèle== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | Le modèle de Normand | + | Le modèle de Normand pose des problèmes concernant sa validité statistique. Il repose en effet sur la recherche de relations statistiques entre des variables aléatoires qui sont dépendantes les unes des autres (l'intensité maximum en 15 minutes et corrélée avec l'intensité maximum en 30 minutes). L'approche correcte consisterait justement à travailler sur la façon dont la corrélation diminue entre les variables lorsque la différence de durée d'analyse augmente. |
| − | sa validité statistique. Il repose en effet sur la recherche de relations entre | + | |
| − | + | ||
| − | et | + | |
| − | [[Catégorie: | + | De plus les données utilisées au moment du développement du modèle (fin des années 1970) était encore peu nombreuses. |
| + | |||
| + | Malgré tout il présente l'intérêt empirique de montrer clairement que les pluies observées n'ont effectivement pas la même période de retour pour toutes les durées d'analyse. Par exemple une pluie dont la période de retour est de 10 ans en 15 minutes, aura généralement une période de retour inférieure à 5 ans en 1 heure. | ||
| + | |||
| + | <u>Bibliographie</u> : | ||
| + | * Deutsch, J.-C. (coordonnateur) (1989) : Mémento sur l'évacuation des eaux pluviales ; La documentation française ; Paris ; 349 p. | ||
| + | * Normand, D., Veyrat, P (1976) : Étude statistique des hyétogrammes types ; rapport SOGREAH R10943 ; Service central hydrologique ; Paris. | ||
| + | |||
| + | [[Catégorie:Dictionnaire_DEHUA]] | ||
| + | [[Catégorie:Modélisation_de_la_pluie_(HU)]] | ||
Version actuelle en date du 3 mars 2025 à 13:32
Traduction anglaise : Normand's model
Dernière mise à jour : 03/03/2025
Mode de construction de pluies de projet, dérivé du modèle de Chicago, tenant compte du fait que la période de retour d'une pluie n'est pas la même pour toutes les durées d'analyse.
[modifier] Principes du modèle
Le modèle de Normand a été établi à partir d'une analyse des intensités moyennes maximales calculées sur des pluies observées (Normand & Veyrat, 1976). Cette analyse a permis de déterminer les périodes de retour (inférieures à 10 ans) qu'il fallait prendre en compte pour des durées, $ t_2 $, inférieures ou supérieures à la durée, $ t_1 $, pour laquelle on avait choisi une période de retour décennale. Les conclusions sont synthétisées dans l'abaque de la figure 1.
[modifier] Intérêt et limite du modèle
Le modèle de Normand pose des problèmes concernant sa validité statistique. Il repose en effet sur la recherche de relations statistiques entre des variables aléatoires qui sont dépendantes les unes des autres (l'intensité maximum en 15 minutes et corrélée avec l'intensité maximum en 30 minutes). L'approche correcte consisterait justement à travailler sur la façon dont la corrélation diminue entre les variables lorsque la différence de durée d'analyse augmente.
De plus les données utilisées au moment du développement du modèle (fin des années 1970) était encore peu nombreuses.
Malgré tout il présente l'intérêt empirique de montrer clairement que les pluies observées n'ont effectivement pas la même période de retour pour toutes les durées d'analyse. Par exemple une pluie dont la période de retour est de 10 ans en 15 minutes, aura généralement une période de retour inférieure à 5 ans en 1 heure.
Bibliographie :
- Deutsch, J.-C. (coordonnateur) (1989) : Mémento sur l'évacuation des eaux pluviales ; La documentation française ; Paris ; 349 p.
- Normand, D., Veyrat, P (1976) : Étude statistique des hyétogrammes types ; rapport SOGREAH R10943 ; Service central hydrologique ; Paris.
 S'abonner à un flux RSS
S'abonner à un flux RSS