Keifer (pluie de projet de) (HU) : Différence entre versions
(→Intérêt et limites) |
|||
| Ligne 1 : | Ligne 1 : | ||
| − | ''<u>Traduction anglaise</u> | + | ''<u>Traduction anglaise</u> : Keifer's design storm'' |
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 24/04/2022 |
[[Hyétogramme (HU)|Hyétogramme]] synthétique, construit à partir des courbes [[Intensité-durée-fréquence / IDF (HU)|Intensité-durée-fréquence]] (IDF), et tel que l'intensité moyenne maximum de pluie ait la même [[Période de retour (HU)|période de retour]] quelle que soit la durée d'analyse (Keifer & Chu, 1957). | [[Hyétogramme (HU)|Hyétogramme]] synthétique, construit à partir des courbes [[Intensité-durée-fréquence / IDF (HU)|Intensité-durée-fréquence]] (IDF), et tel que l'intensité moyenne maximum de pluie ait la même [[Période de retour (HU)|période de retour]] quelle que soit la durée d'analyse (Keifer & Chu, 1957). | ||
| − | == Principes de | + | == Principes de construction : cas d'un hyétogramme toujours décroissant == |
| − | Considérons un hyétogramme synthétique tel que le maximum d'intensité soit situé à l'origine des temps (averse de type complètement avancée). Quel que soit le temps considéré, inférieur ou égal à la durée de l'averse, on peut | + | Considérons un hyétogramme synthétique tel que le maximum d'intensité soit situé à l'origine des temps (averse de type complètement avancée). Quel que soit le temps considéré, inférieur ou égal à la durée de l'averse, on peut écrire : |
| Ligne 15 : | Ligne 15 : | ||
avec : | avec : | ||
| − | |||
* <math>i(τ)</math> intensité instantanée ; | * <math>i(τ)</math> intensité instantanée ; | ||
* <math>i_{moy}</math>, intensité moyenne sur la durée <math>t</math> ; | * <math>i_{moy}</math>, intensité moyenne sur la durée <math>t</math> ; | ||
| − | A partir des courbes IDF, et connaissant la période de retour <math>T</math>, on peut évaluer <math>i_{moy}</math> en fonction de <math>T</math>. Par exemple si l'on utilise un ajustement de type [[Montana (formule type) (HU)|Montana]] | + | A partir des courbes IDF, et connaissant la période de retour <math>T</math>, on peut évaluer <math>i_{moy}</math> en fonction de <math>T</math>. Par exemple si l'on utilise un ajustement de type [[Montana (formule type) (HU)|Montana]] : |
| Ligne 25 : | Ligne 24 : | ||
| − | En dérivant les deux termes de l'équation (1) on | + | En dérivant les deux termes de l'équation (1) on obtient : |
| − | <center><math>\frac{d}{dt}\left(\int_0^t{i(τ)}.dτ | + | <center><math>\frac{d}{dt}\left(\int_0^t{i(τ)}.dτ\right)=\frac{d}{dt}\left(i_{moy}.t\right)=\frac{d}{dt}\left(a(T).t^{b(T+1)}\right) \quad (2)</math></center> |
| − | + | soit : | |
| Ligne 48 : | Ligne 47 : | ||
== Généralisation à une position quelconque du maximum == | == Généralisation à une position quelconque du maximum == | ||
| − | En réalité, pour une pluie réelle, on peut considérer deux | + | En réalité, pour une pluie réelle, on peut considérer deux périodes : |
| − | * l'une précédant la pointe d'intensité, de durée <math> | + | * l'une précédant la pointe d'intensité, de durée <math>t_a = r.t_d</math> (si <math>t_d</math> est la durée totale de la pluie), |
| − | * l'autre suivant la pointe d'intensité, de durée <math> | + | * l'autre suivant la pointe d'intensité, de durée <math>t_p = (1 - r).t_d</math>. |
| − | Le coefficient <math>r</math>, compris entre 0 et 1 caractérise la forme du | + | Le coefficient <math>r</math>, compris entre 0 et 1 caractérise la forme du hyétogramme ; il peut se déduire d'une analyse statistique de la forme d'un échantillon représentatif de pluies réelles. A partir de l'analyse d'averses orageuses enregistrées sur la ville de Chicago, Keifer a ainsi proposé de donner la valeur 0,5 à <math>r</math>. Les calculs se mènent comme précédemment, les intégrales étant calculées entre <math>- r.t</math> et (<math>1 - r).t</math> : |
| Ligne 65 : | Ligne 64 : | ||
== Intérêt et limites == | == Intérêt et limites == | ||
| − | Cette méthode est intéressante par sa simplicité et son caractère | + | Cette méthode est intéressante par sa simplicité et son caractère pédagogique ; elle présente cependant plusieurs inconvénients : |
| − | * elle repose sur l'hypothèse que toutes les pluies, quelle que soit leur durée, ont la même forme ce qui est | + | * elle repose sur l'hypothèse que toutes les pluies, quelle que soit leur durée, ont la même forme ce qui est faux ; |
| − | * la valeur retenue pour <math>r</math> est généralement la valeur moyenne | + | * la valeur retenue pour <math>r</math> est généralement la valeur moyenne observée ; or il semblerait que la position du maximum soit régie par une loi sensiblement uniforme sur l'intervalle <math>[0{,}1] </math>; les valeurs voisines de <math>0{,}5</math>, généralement retenues, ne seraient donc pas plus probables que les valeurs 0 ou 1 ; |
| − | * enfin et surtout, la période de retour que l'on doit attacher à un tel événement pluviométrique est supérieure à la période de retour de la courbe IDF à partir duquel il a été construit. En effet, du fait du mode de construction, la pluie a la même période de retour quelle que soit la durée d'analyse, ce qui n'est pas le cas d'une pluie réelle. La période de retour réelle des débits générés par un tel événement pluvieux est donc également supérieure à celle | + | * enfin et surtout, la période de retour que l'on doit attacher à un tel événement pluviométrique est supérieure à la période de retour de la courbe IDF à partir duquel il a été construit. En effet, du fait du mode de construction, la pluie a la même période de retour quelle que soit la durée d'analyse, ce qui n'est pas le cas d'une pluie réelle. La période de retour réelle des débits générés par un tel événement pluvieux est donc également supérieure à celle escomptée ; elle est de plus difficile à déterminer. |
| − | <u>Bibliographie</u> | + | <u>Bibliographie</u> : |
| − | * | + | * Keifer, D.J., Chu, H.H. (1957) : ‘’Synthetic Storm Pattern for Drainage Design’’ ; ASCE Journal of the Hydraulics Division, Vol. 83 (HY4), pp 1332.1-1332.25. |
[[Catégorie:Dictionnaire_DEHUA]] | [[Catégorie:Dictionnaire_DEHUA]] | ||
[[Catégorie:Modélisation_de_la_pluie_(HU)]] | [[Catégorie:Modélisation_de_la_pluie_(HU)]] | ||
Version du 24 avril 2022 à 09:30
Traduction anglaise : Keifer's design storm
Dernière mise à jour : 24/04/2022
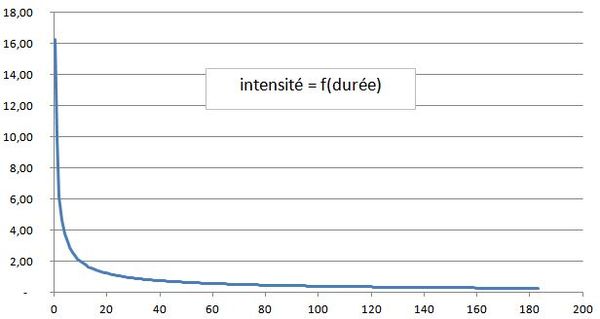
Hyétogramme synthétique, construit à partir des courbes Intensité-durée-fréquence (IDF), et tel que l'intensité moyenne maximum de pluie ait la même période de retour quelle que soit la durée d'analyse (Keifer & Chu, 1957).
Principes de construction : cas d'un hyétogramme toujours décroissant
Considérons un hyétogramme synthétique tel que le maximum d'intensité soit situé à l'origine des temps (averse de type complètement avancée). Quel que soit le temps considéré, inférieur ou égal à la durée de l'averse, on peut écrire :
avec :
- $ i(τ) $ intensité instantanée ;
- $ i_{moy} $, intensité moyenne sur la durée $ t $ ;
A partir des courbes IDF, et connaissant la période de retour $ T $, on peut évaluer $ i_{moy} $ en fonction de $ T $. Par exemple si l'on utilise un ajustement de type Montana :
En dérivant les deux termes de l'équation (1) on obtient :
soit :
Nota : un calcul identique peut être fait avec d'autres expressions littérales de $ i_{moy} $ en fonction de $ t $ et $ T $.
Ces relations donnent la forme d'un hyétogramme correspondant à une pluie de type complètement avancé (monotone décroissante).
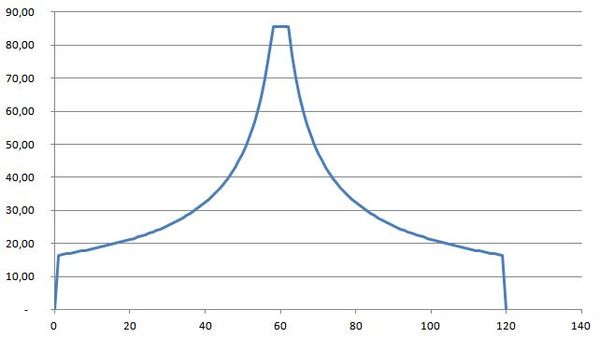
Généralisation à une position quelconque du maximum
En réalité, pour une pluie réelle, on peut considérer deux périodes :
- l'une précédant la pointe d'intensité, de durée $ t_a = r.t_d $ (si $ t_d $ est la durée totale de la pluie),
- l'autre suivant la pointe d'intensité, de durée $ t_p = (1 - r).t_d $.
Le coefficient $ r $, compris entre 0 et 1 caractérise la forme du hyétogramme ; il peut se déduire d'une analyse statistique de la forme d'un échantillon représentatif de pluies réelles. A partir de l'analyse d'averses orageuses enregistrées sur la ville de Chicago, Keifer a ainsi proposé de donner la valeur 0,5 à $ r $. Les calculs se mènent comme précédemment, les intégrales étant calculées entre $ - r.t $ et ($ 1 - r).t $ :
Il est également nécessaire de faire un traitement spécifique au voisinage de la pointe d'intensité pour éviter des intensités tendant vers l'infini. En général on considère un plateau de durée égal au plus petit pas de temps pour lequel l'ajustement est valable (souvent 6 minutes en hydrologie urbaine).
Intérêt et limites
Cette méthode est intéressante par sa simplicité et son caractère pédagogique ; elle présente cependant plusieurs inconvénients :
- elle repose sur l'hypothèse que toutes les pluies, quelle que soit leur durée, ont la même forme ce qui est faux ;
- la valeur retenue pour $ r $ est généralement la valeur moyenne observée ; or il semblerait que la position du maximum soit régie par une loi sensiblement uniforme sur l'intervalle $ [0{,}1] $; les valeurs voisines de $ 0{,}5 $, généralement retenues, ne seraient donc pas plus probables que les valeurs 0 ou 1 ;
- enfin et surtout, la période de retour que l'on doit attacher à un tel événement pluviométrique est supérieure à la période de retour de la courbe IDF à partir duquel il a été construit. En effet, du fait du mode de construction, la pluie a la même période de retour quelle que soit la durée d'analyse, ce qui n'est pas le cas d'une pluie réelle. La période de retour réelle des débits générés par un tel événement pluvieux est donc également supérieure à celle escomptée ; elle est de plus difficile à déterminer.
Bibliographie :
- Keifer, D.J., Chu, H.H. (1957) : ‘’Synthetic Storm Pattern for Drainage Design’’ ; ASCE Journal of the Hydraulics Division, Vol. 83 (HY4), pp 1332.1-1332.25.
 S'abonner à un flux RSS
S'abonner à un flux RSS