ANSWER - Modèle de propagation des ondes longues

Eléments de contexte

Le Groupement d'Intérêt Scientifique "Hydraulique pour l'Ecologie et le Développement durable" (GIS HED2) initie une action collaborative de recensement de solutions analytiques dans le domaine de la mécanique des fluides à surface libre. L'objectif de ce recensement est multiple :

• il permet de disposer d'une base de référence de cas très simples, qui constituent des simplifications des équations de base et qui permettent de caler des codes de calcul
• il peut servir d'accompagnement de programmes de formation pour des techniciens, ingénieurs et chercheurs qui souhaitent disposer d'une information très accessible et concentrée en un site

Pour atteindre cet objectif, chaque fiche comprend un rappel des simplifications réalisées, l'expression des modèles simplifiés, la solution analytique correspondante, la résolution d'un problème simple, une proposition de montage en laboratoire et une proposition de réalisation d'images ou de films en nature pour illustrer ce processus. Pour cela, un ensemble de 2 fiches types sont réalisées : l'une théorique (fiche à venir) explicite la méthode d'obtention de la solution analytique, la seconde, plus pratique concerne le traitement de la solution analytique (qui constitue la présente page).

Hiérarchie des hypothèses simplificatrices

Navier-Stokes

→ fluide incompressible

→ intégration dans une section de calcul (canal rectangulaire) ==> Saint-Venant 1D

→ accélération négligeable

→ frottement négligeable

Expression de l'équation simplifiée

A partir des hypothèses précédentes, considérons un canal infini de forme rectangulaire : largeur $ b $ et profondeur d'eau $ H $.
Soit $ h $ le niveau d'eau, $ u $ la vitesse moyenne de l'écoulement dans la section de surface $ A = bH $ et enfin $ Q=bHu $ le débit, les équations simplifiées prennent la forme suivante :

$ \begin{cases} \dfrac{ \partial h }{ \partial t }+H \dfrac{ \partial u }{ \partial x }=0 } \\ \\ \dfrac{ \partial u }{ \partial t }+g \dfrac{ \partial h }{ \partial x }=0 \end{cases} $ Si l'on dérive la première équation par rapport à $ t $ et la seconde par rapport à $ x $, et en éliminant le terme $ \dfrac{ \partial^2 u }{ \partial t \partial t } $

Nous obtenons l'équation des ondes suivante: $ \dfrac{ \partial^2 h }{ \partial t^2 }-gH \dfrac{ \partial^2 h }{ \partial x^2 } $

Expression de la solution analytique

Cette équation peut se mettre sous la forme: $ (\dfrac{ \partial h }{ \partial t }-c \dfrac{ \partial h }{ \partial x }) ( \dfrac{ \partial h }{ \partial t }+c \dfrac{ \partial h }{ \partial x })=0 $ Une solution de cette équation pour l'évolution de la surface libre est la suivante:
$ h=acos(kx-\sigma t) $ qui correspond à la propagation de 2 ondes de vitesse $ c= \sqrt{gH} $ dans les deux sens (vers la gauche et vers la droite)

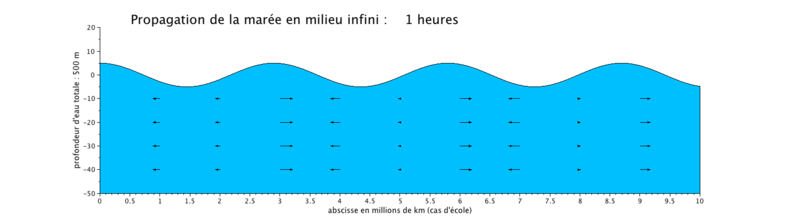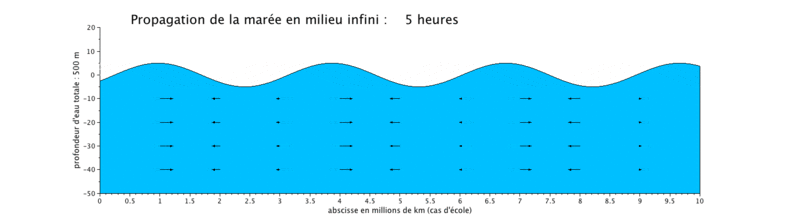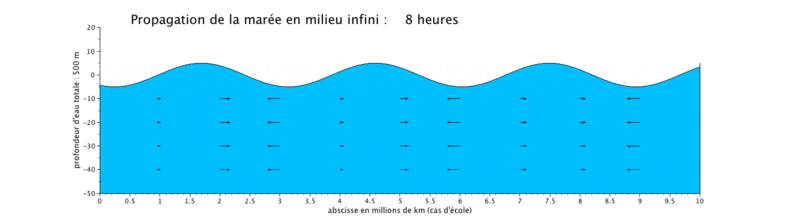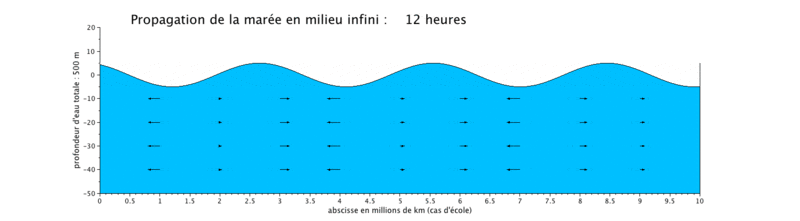
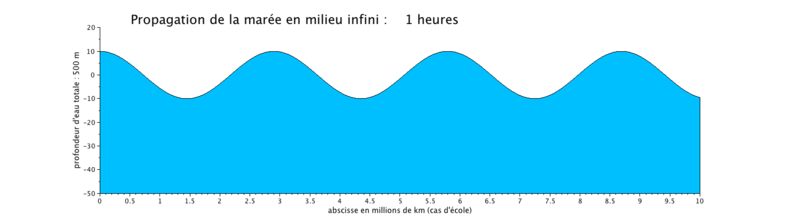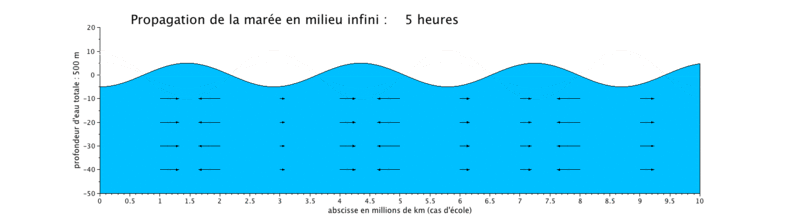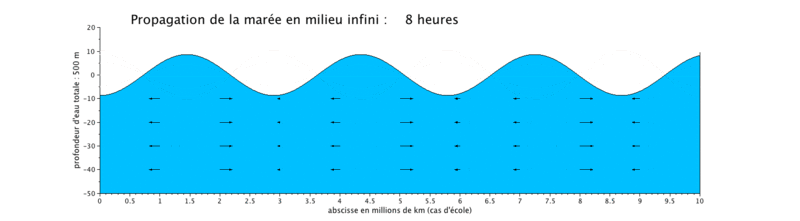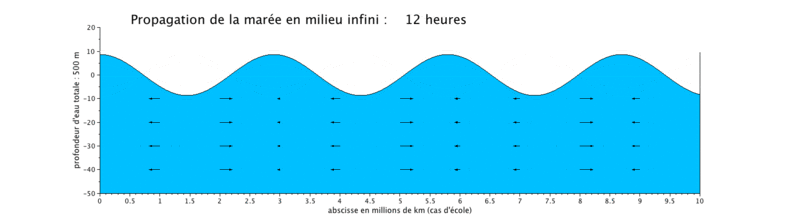
Cas d'application : translation d'une onde sinusoïdale

Onde de marée progressive

Le cas que nous présentons ici est un cas d'école, car il met en scène la propagation d'une onde de marée de période de 12 heures dans un canal long de $ 10^7) $ ceci pour illustrer plusieurs longueurs d'onde sur une même figure.
Les caractéristiques de cet exemple sont les suivants:

• période de la marée : 12 heures
• amplitude : 5m
• profondeur : 500 m

Les calculs conduisent à:

• longueur d'onde : 2897 m
• célérité : 67 m/s
• nombre d'onde : 0.0000022 m-1

Le champ de vitesse peut être obtenu en remplaçant l'expression de la surface libre $ h(x,t) $ dans l'équation de continuité. En dérivant l'expression de $ h(x,t) $ par rapport à $ t $ et en l'intégrant par rapport à $ x $, nous obtenons l'expression de la vitesse:
$ h=\dfrac{ a\sigma }{ dk } \cos(kx-\sigma t) $

Onde de marée stationnaire

Le cas de l'onde marée stationnaire correspond à la rencontre de deux ondes de même période mais de sens opposé. Ces deux ondes ont les caractéristiques précédentes. Les expressions de la variation du niveau d'eau et de la vitesse sont les suivants:

$ h=2a \cos kx \cos\sigma t $ et $ h=2\dfrac{ agk}{ \sigma } \sin kx \sin\sigma t $

Remarquons que dans ce cas, niveau d'eau et vitesse sont en opposition de phase.

Conclusions

D'après les exemples précédents, nous pouvons mettre ne évidence les processus suivant:

• la propagation de l'onde progressive se fait avec une vitesse de courant en phase avec le niveau d'eau, ce qui signifie que lorsque le niveau d'eau est maximal, c'est-à-dire en haute mer (respectivement minimal en basse mer), la vitesse du courant est maximale (respectivement minimale). Les vitesses sont minimales à mi-montant et à mi-perdant. Ceci se produit donc en haute mer.
• par contre, et c'est vraiment ce qui se passe dans les estuaires, la situation est complètement opposée pour l'onde stationnaire. Dans ce cas, niveau d'eau et vitesse sont en opposition de phase. Ainsi, lorsque le niveau est maximal (pleine mer) ou minimal (basse mer), les vitesses sont nulles. Ces vitesses sont maximales à mi-montant et à mi-perdant.

Bibliographie

A compléter