ANSWER - Modèle de propagation des ondes longues

Eléments de contexte

Le graphe PEARLTREES ci-dessous illustre les solutions analytiques envisageables (perles blanches) et celles qui sont déjà disponibles (perles avec motif).
Pour visualiser une page rédigée, cliquer sur l'une des perles actives.
Pour visualiser le contexte général des 4 branches:

• hydraulique fluviale
• hydraulique maritime
• hydrogéologie
• morphodynamique

cliquer ici

Le Groupement d'Intérêt Scientifique "Hydraulique pour l'Ecologie et le Développement durable" (GIS HED2) initie une action collaborative de recensement de solutions analytiques dans le domaine de la mécanique des fluides à surface libre. L'objectif de ce recensement est multiple :

• il permet de disposer d'une base de référence de cas très simples, qui constituent des simplifications des équations de base et qui permettent de caler des codes de calcul
• il peut servir d'accompagnement de programmes de formation pour des techniciens, ingénieurs et chercheurs qui souhaitent disposer d'une information très accessible et concentrée en un site

Pour atteindre cet objectif, chaque fiche comprend un rappel des simplifications réalisées, l'expression des modèles simplifiés, la solution analytique correspondante, la résolution d'un problème simple, une proposition de montage en laboratoire et une proposition de réalisation d'images ou de films en nature pour illustrer ce processus. Pour cela, un ensemble de 2 fiches types sont réalisées : l'une théorique (fiche à venir) explicite la méthode d'obtention de la solution analytique, la seconde, plus pratique concerne le traitement de la solution analytique (qui constitue la présente page).

Hiérarchie des hypothèses simplificatrices

Navier-Stokes

→ fluide incompressible

→ intégration dans une section de calcul (canal rectangulaire) ==> Saint-Venant 1D

→ accélération négligeable

→ frottement négligeable

Expression de l'équation simplifiée

A partir des hypothèses précédentes, considérons un canal infini de forme rectangulaire : largeur $ b $ et profondeur d'eau $ H $.
Soit $ h $ le niveau d'eau, $ u $ la vitesse moyenne de l'écoulement dans la section de surface $ A = bH $ et enfin $ Q=bHu $ le débit, les équations simplifiées prennent la forme suivante :

$ \begin{cases} \dfrac{ \partial h }{ \partial t }+H \dfrac{ \partial u }{ \partial x }=0 } \\ \\ \dfrac{ \partial u }{ \partial t }+g \dfrac{ \partial h }{ \partial x }=0 \end{cases} $

Si l'on dérive la première équation par rapport à $ t $ et la seconde par rapport à $ x $, et en éliminant le terme $ \dfrac{ \partial^2 u }{ \partial x \partial t } $, nous obtenons l'équation des ondes suivante: $ \dfrac{ \partial^2 h }{ \partial t^2 }-gH \dfrac{ \partial^2 h }{ \partial x^2 }=0 $

Expression de la solution analytique

Cette équation peut se mettre sous la forme: $ (\dfrac{ \partial h }{ \partial t }-c \dfrac{ \partial h }{ \partial x }) ( \dfrac{ \partial h }{ \partial t }+c \dfrac{ \partial h }{ \partial x })=0 $ Une solution de cette équation pour l'évolution de la surface libre est la suivante:
$ h=acos(kx-\sigma t) $ qui correspond à la propagation de 2 ondes de vitesse $ c= \sqrt{gH} $ dans les deux sens (vers la gauche et vers la droite)

Cas d'application : translation d'une onde sinusoïdale

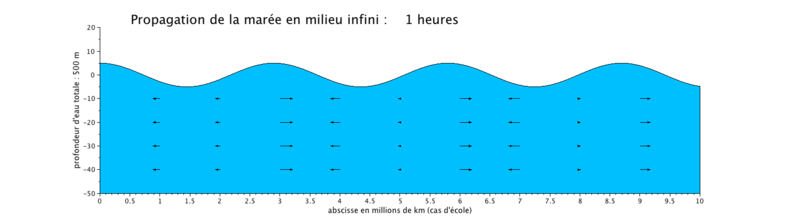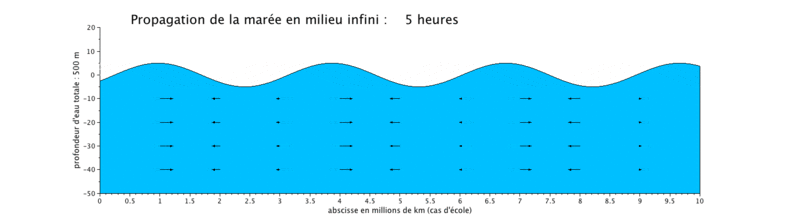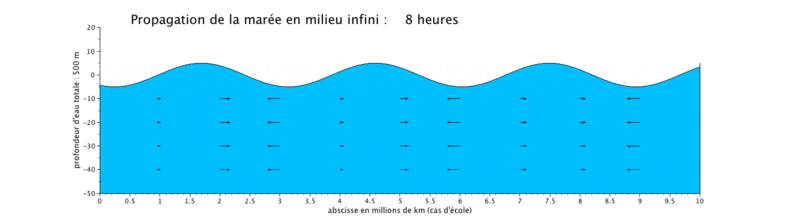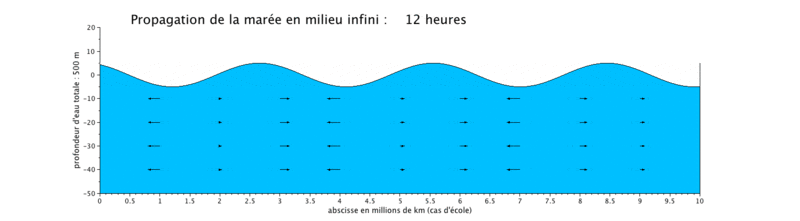
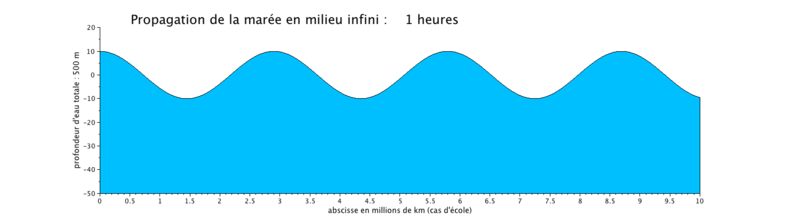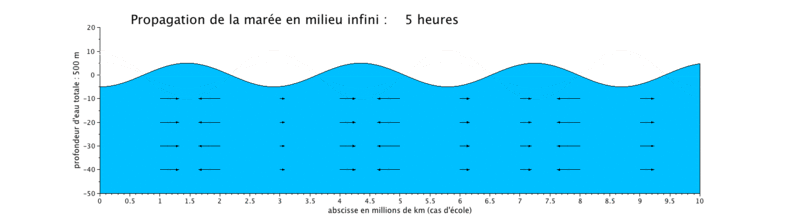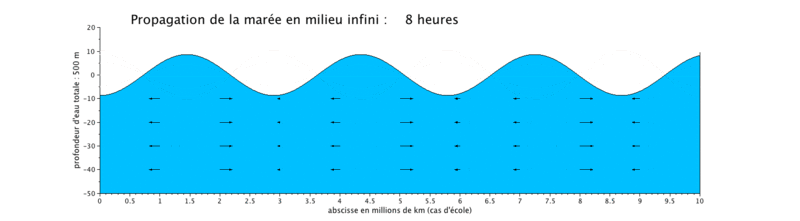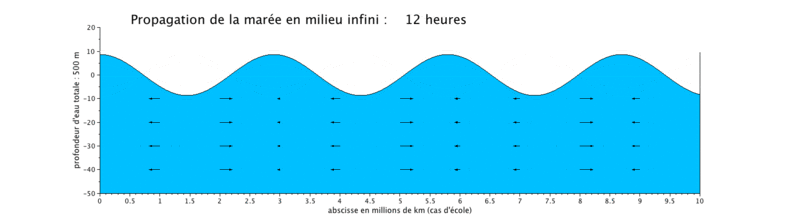
Onde de marée progressive

Le cas que nous présentons ici est un cas d'école, car il met en scène la propagation d'une onde de marée de période de 12 heures dans un canal infini (ici limité à $ 10^7 $ m, ceci pour illustrer plusieurs longueurs d'onde sur une même figure).
Les caractéristiques de cet exemple sont les suivants:

• période de la marée : 12 heures
• amplitude : 5m
• profondeur : 500 m (la profondeur sur les représentations graphiques a été limitée à 50 m pour des questions de lisibilité)

Les calculs conduisent à:

• longueur d'onde : 2897 m
• célérité : 67 m/s
• nombre d'onde : 0.0000022 m-1

Le champ de vitesse peut être obtenu en remplaçant l'expression de la surface libre $ h(x,t) $ dans l'équation de continuité. En dérivant l'expression de $ h(x,t) $ par rapport à $ t $ et en l'intégrant par rapport à $ x $, nous obtenons l'expression de la vitesse:
$ u=\dfrac{ a\sigma }{ dk } \cos(kx-\sigma t) $

Onde de marée stationnaire

Le cas de l'onde marée stationnaire correspond à la rencontre de deux ondes de même période mais de sens opposé. Ces deux ondes ont les caractéristiques précédentes. Les expressions de la variation du niveau d'eau et de la vitesse sont les suivantes:

$ h=2a \cos kx \cos\sigma t $

$ u=2\dfrac{ agk}{ \sigma } \sin kx \sin\sigma t $

Remarquons que dans ce cas, niveau d'eau et vitesse sont en opposition de phase.

Essai en laboratoire

Des essais en laboratoires peuvent être envisagés en respectant la similitude de Froude.

Observation en nature

Des videos en nature ou des résultats de modèles numériques sur le propagation de la marée (marée en Manche par exemple) ou de résonance (Baie de Fundy au Canada) pourraient donner une vision dynamique et réaliste du phénomène.

Conclusions

D'après les exemples précédents, nous pouvons mettre en évidence les processus suivants:

• la propagation de l'onde progressive se fait avec une vitesse de courant en phase avec le niveau d'eau, ce qui signifie que lorsque le niveau d'eau est maximal, c'est-à-dire en haute mer (respectivement minimal en basse mer), la vitesse du courant est maximale (respectivement minimale). Les vitesses sont minimales à mi-montant et à mi-perdant. Ceci se produit donc en haute mer.
• par contre, et c'est vraiment ce qui se passe dans les estuaires, la situation est complètement opposée pour l'onde stationnaire. Dans ce cas, niveau d'eau et vitesse sont en opposition de phase. Ainsi, lorsque le niveau est maximal (pleine mer) ou minimal (basse mer), les vitesses sont nulles. Ces vitesses sont maximales à mi-montant et à mi-perdant.
• plusieurs auteurs (Le Méhauté, 1976) ont considéré que la théorie des ondes longues pouvait être considérée comme la limite de la théorie de la propagation des ondes en eaux profondes. Ceci était probablement justifié par l'équation de la surface libre qui est dans les deux cas de la forme $ h=acos(kx-\sigma t) $. La similitude s'arrête là, car le patron des vitesses est très différent : très rapidement dégressif pour les ondes de surface et constant dans toute la verticale et jusqu'au fond pour les ondes longues. Enfin, il n'y a pas de transfert de masse pour les ondes de surface alors qu'il y en a pour les ondes longues.

Bibliographie

• Le Méhauté B., "An Introduction to Hydrodynamics & Waterways" Springer-Verlag, 1976, 315 p.
• Thual O., "Hydrodynamique de l'environnement", Les éditions de l'Ecole Polytechnique, Oct. 2011, 314 p.
• Dinguemans M. W., "Water Wave Propagation Over Uneven Bottoms - Part 1 - Linear Wave Propagation", Advanced Series on Ocean Engineering - Volume 13, World Scientific, 471 p.
• Dinguemans M. W., "Water Wave Propagation Over Uneven Bottoms - Part 2 - Non-Linear Wave Propagation", Advanced Series on Ocean Engineering - Volume 13, World Scientific, 494 p.
• site du SHOM et plus particulièrement une page dédiée aux courants de marée

code Scilab

// propagation d'onde en eaux peu profondes
// Canal ouvert à droite (istat=0) ou stationnaire (istat=1)
clf()
LONG=10000000; // longueur du canal
fact=1000000 // facteur d'échelle pour représentation des vecsteurs vitesse
istat=0 // onde stationnaire (0) ou non (1)
a=5;// amplitude de l'onde
yminaffich=-50 //affiche la profondeur jusqu'à une profondeur de 50 m
b=get("current_axes");
b.data_bounds=[0,yminaffich;LONG/fact,6];
c=b.children
d=gca() //définition des axes
d.data_bounds=[0,-50;10,20];
d.axes_visible = 'on';
d.labels_font_size=2;
d.x_label.font_size = 3;d.y_label.font_size = 3;
d.x_label.text="abscisse en millions de km (cas d''école)"
d.y_label.text="profondeur d''eau totale : 500 m"
// fixer la couleur du champ de vecteur à "blanc"
f=gcf()
f.color_map=wintercolormap(32)
// définit les dimensions de la figure
f.figure_position
f.figure_size=[1500,500]
c=b.children
title('Propagation de la marée en milieu infini','position',[0.5 20],'fontsize',5)
// données
g=9;81 // gravite
T=12*3600; // période de l'onde
d=500; //profondeur d'eau 
C=sqrt(g*d);// célérité de l'onde
L=T*C;//longueur d'onde
k=2*%pi/L ;// nombre d'onde
x=0:LONG/1000:LONG //discrétisation suivant x
sigma=2*%pi/T // fréquence
coefu=a*g*k/sigma // utilisé pou la vitesse
//couleurs des aires des courbes
id1=color('white')
id2=color(0,191,255) 
 
//==============================================================================
i=0
for t=0:3600:12*3600
 
    // fixer la couleur du champ de vecteur à "blanc"
    i=i+1
    if i<>1 then yprec=y; end
    y=a*cos(k*x-sigma*t)
    if istat==1 then y=y+a*cos(k*x+sigma*t)
    end
    if i==1 then yprec=y; end
    xfpolys([x'/fact;LONG/fact;0],[yprec';yminaffich;yminaffich],[id1])
    plot(x'/fact,yprec',"w")
    xfpolys([x'/fact;LONG/fact;0],[y';yminaffich;yminaffich],[id2]) 
    deltay=max(y,yprec)
    num=string(i)
    xpause(100000);
    title('Propagation de la marée en milieu infini :...
    '+num+ ' heures','position',[0.5 20],'fontsize',5)
 
    // dessin des vecteurs vitesse
    xvect=[1 2 3 4 5 6 7 8 9 20];yvect=[-40:10:-10]
    fvarx=coefu*cos(k*xvect*fact-sigma*t);
    if istat==1 then fvarx=fvarx-coefu*cos(k*xvect*fact+sigma*t); end
    fvarx(10)=3;  
    fx=fvarx'*ones(1,4);fy=zeros(10,4);
    // tracé des vecteurs vitesse
    champ(xvect',yvect',fx,fy,arfact=1,rect=[0,-50,10,20])
 
    //GIF export
    xs2gif(0,'Marée_'+string(i)+'.gif');
 
end

Le créateur de cet article est Jean-Michel Tanguy Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. Pour d'autres articles de cet auteur, voir ici. Pour un aperçu des contributions de cet auteur, voir ici.