A.10 - Intervalles de prévision

Définition

Au lieu de donner une valeur unique à la grandeur à prévoir, ou de fournir quelques valeurs en indiquant la probabilité associée à chaque valeur, il peut être intéressant de donner un intervalle en indiquant la probabilité que la valeur de la grandeur à prévoir soit comprise dans cet intervalle.

Si on cherche à prévoir à l'instant t la valeur qu'aura la grandeur X à t + H (qu'on peut noter ) alors l'intervalle [a,b] est un intervalle de prévision de à y % si ;

En notant la densité de probabilité associée à la valeur x (fiche A.08).

Par convention, on définit l'intervalle de prévision centré à y % par la probabilité que la grandeur à prévoir se situe au-dessous de la borne inférieure a et celle qu'elle se situe au-dessus de la borne supérieure b :

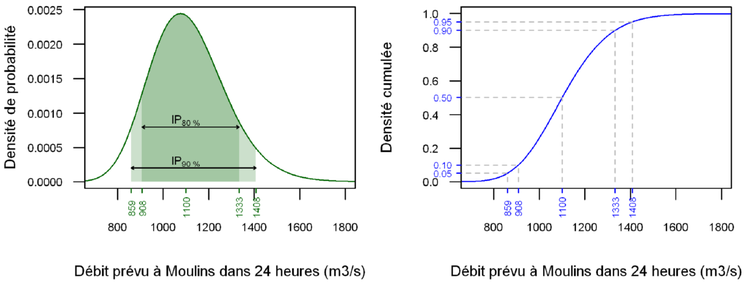
Exemple 1. Le débit à Moulins dans 24 h n'est pas connu avec certitude (sinon les prévisionnistes seraient au chômage). Donner comme intervalle de prévision à 90 %, l'intervalle 860 – 1 410 m3/s revient à affirmer qu'il y a 9 chances sur 10 que le débit à venir dans 24 h sera compris entre 859 et 1 408 m3/s. La figure ci-dessous représente les intervalles de prévision à 80 % et 90 % pour le débit prévu à Moulins dans 24 heures. La probabilité que le débit soit compris entre 910 et 1 330 m3/s est de 80 % : l'intervalle de prévision à 80 % est plus petit que l'intervalle de prévision à 90 %.

Quelle utilité pour l'affichage des prévisions sur Vigicrues ?

Les tendances « basses » et « hautes » que nous avons à représenter pour « encadrer » la prévision déterministe sur les hydrogrammes et limnigrammes communiqués sur Vigicrues peuvent être définies comme étant les bornes (a et b) d'un intervalle de prévision à x % (avec x de l'ordre de 0,9 par exemple). Cette approche permet de fournir une information compréhensible de façon précise (unique) par les utilisateurs de Vigicrues (et donc d'éviter des confusions, potentiellement néfastes dans la prise de décisions basées sur cette information).

Intervalles de prévision, intervalles de confiance : quelle différence ?

L'expression « intervalle de confiance » est souvent employée à la place d' « intervalle de prévision ». Même si la confusion n'est pas gênante dans la majorité des cas, les statisticiens donnent des sens bien différents à ces expressions : L'intervalle de prévision est utilisé pour décrire notre connaissance pour un événement unique à venir (notre prévision). Cette prévision est formalisée comme étant une réalisation d'une variable aléatoire (ainsi, dans l'exemple 1, on ne s'intéresse qu'à une seule valeur : celle du débit à Moulins dans 24 h). L'intervalle de confiance à y % est l'intervalle dans lequel un paramètre (une caractéristique) d'une distribution de probabilité ou d'une population inconnue a une probabilité y/100 de se trouver.

Exemple 2. Un statisticien s'intéresse à la taille des Français majeurs. Pour cela, il réalise un sondage de 2 000 individus (pris au hasard) et collecte ainsi un échantillon de leurs tailles. La moyenne calculée sur cet échantillon donne une information sur la taille moyenne de l'ensemble des Français entre 1960 et 2000, mais n'est vraisemblablement pas exactement la moyenne de la taille des Français majeurs. En effet, cet échantillon est très limité par rapport à l'ensemble des Français adultes (plus de 50 millions de personnes). Aussi, en considérant la taille comme une variable aléatoire, la taille moyenne des Français adultes (l'espérance de la variable aléatoire) est approchée par la moyenne statistique calculée sur l'échantillon de 2 000 individus, encadrée par un intervalle de confiance à y %.

Voir également

Fiche A.08 – Probabilités