S'abonner à un flux RSS
A.12 - Mode et distribution multimodale
Mode d'une distribution de probabilité
Considérons une distribution de probabilité d'une variable X de densité 
. Son mode est la valeur Xm de la variable X telle que la densité de probabilité y atteigne sa valeur maximale :
pour toute valeur x de la variable X.
Certaines densités de probabilité classiques sont symétriques et leurs modes sont égaux à leurs médianes (fiche A.09) et à leurs moyennes. C'est par exemple, le cas des densités normales. Mais dans de très nombreux cas, ces trois valeurs caractérisant « l'épicentre » de la distribution ne sont pas égales (exemple 1).
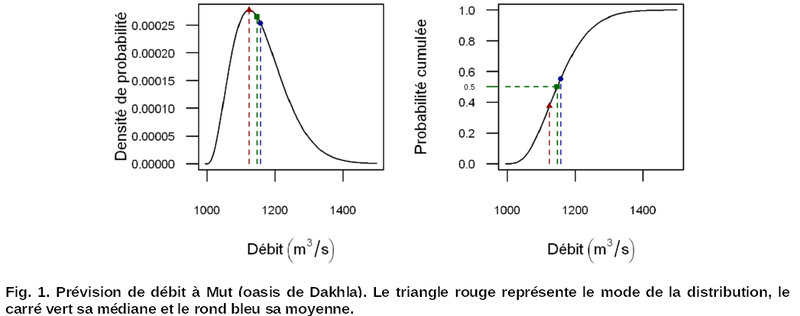
Exemple 1. La figure 1 représente la prévision probabiliste de débit à Mut (oasis de Dakhla) par le SPC Sahara oriental. La distribution prévue est asymétrique et la valeur la plus vraisemblable (le mode, égal à 1 124 m3/s) est sensiblement différent de la médiane (1 chance sur 2 d'être au-dessus de cette valeur, 1 148 m3/s) et de la moyenne (espérance de la prévision, 1 158 m3/s). Selon que le but de la prévision est d'optimiser une production hydroélectrique ou de gérer les conséquences d'un dépassement de seuil, on ne s'intéressera pas à la même caractérisation de l'épicentre de la distribution.
Distribution multimodale
Une distribution est dite multimodale si sa densité présente plusieurs maxima locaux.
La plupart des distributions que nous rencontrons ne sont pas multimodales, à l'image de la distribution de l'exemple 1. Cependant, des distributions multimodales peuvent apparaître en prévision dans certaines circonstances, comme des cours d'eau aménagés (exemple 2), ou encore si la prévision météorologique est complexe et présente une situation « binaire » (exemple 3).
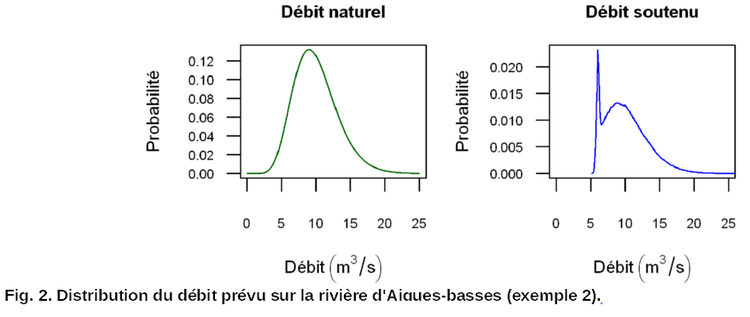
Exemple 2. La rivière d'Aigues-basses est aménagée : un barrage a été élevé à l'amont pour assurer un soutien d'étiage. La consigne du barrage impose de maintenir un débit minimal de 6 m3/s à la station de Puits-Tari. Une prévision d'étiage est organisée sur ce cours d'eau. La figure 2 présente le débit prévu à Puits-Tari si l'écoulement était naturel (sans influence du barrage, à gauche) puis le débit prévu avec soutien d'étiage (à droite). On peut imaginer une situation analogue pour une prévision de crue à l'aval d'un barrage écrêteur en retournant la distribution (mais l'action du barrage serait sans doute moins simple à représenter).
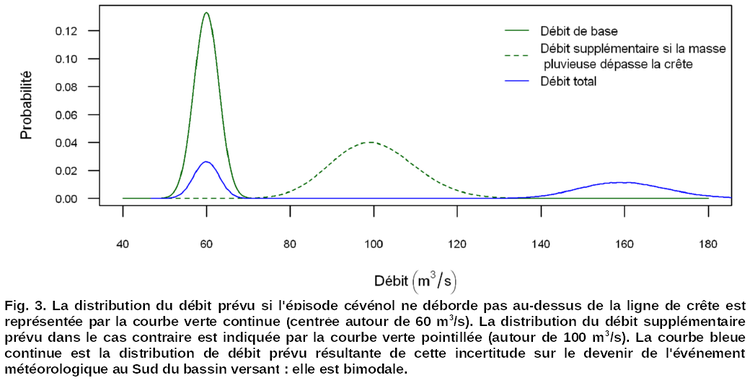
Exemple 3. Le SPC Cévennes-Nord s'intéresse à la prévision de débit d'un cours d'eau prenant sa source dans les contreforts Nord du plateau ardéchois. Le débit de base est de l'ordre de 60 m3/s au niveau de la station. Mais si la cellule orageuse venant de la Méditerranée dépasse la crête ardéchoise et atteint le haut du bassin versant (le cours d'eau coule du Sud vers le Nord), alors des pluies intenses alimenteront la rivière et les prévisionnistes estiment que le débit augmentera de 100 m3/s environ. Lors d'une conférence avec le CMIR, les prévisionnistes apprennent qu'il y a 6 chances sur 10 que la cellule pluvieuse déborde sur le bassin versant. La figure 3 représente les densités de probabilité de prévision correspondantes.
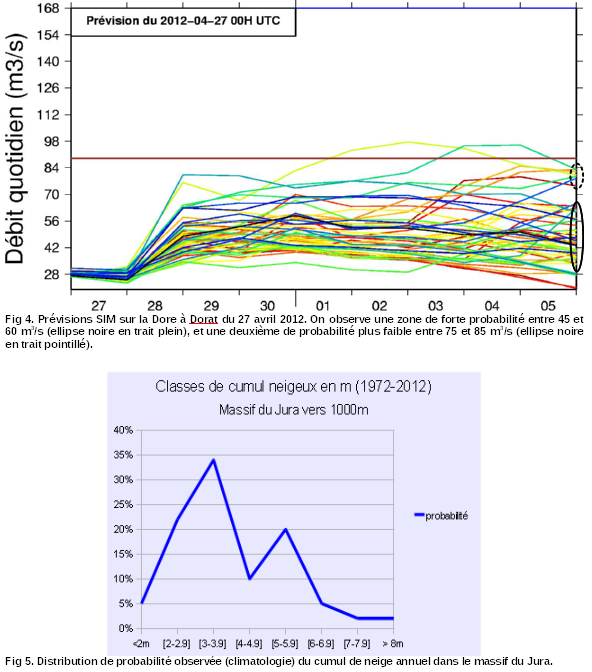
Exemple 4. Les prévisions d'ensemble de pluie peuvent conduire à des distributions de probabilité bimodales. La figure 4 montre une prévision hydrologique par la chaîne de modèles SIM alimentée par les prévisions d'ensemble de précipitation du CEPMMT.
Exemple 5. La distribution de probabilité du cumul de neige annuel dans le Jura, prévu en se basant sur la climatologie est également bimodale (Fig. 5).
Voir également
