ANSWER - Propagation non-linéaire d'un signal de marée dans un estuaire
Sommaire |
Éléments de contexte
Cette page fait partie de la démarche collaborative ANSWER , dont l'objectif est créer les conditions de collaboration entre scientifiques et grand public autour du domaine de l'eau.
Le domaine estuarien présente est un domaine intéressant pour les modélisateurs et plusieurs fiches ont été établies:
- propagation d'une onde longue dans un estuaire à gabarit constant et à fond plat
- propagation dans un estuaire à gabarit constant et à pente du fond inclinée
- propagation d'une onde dans un estuaire à berges convergentes linéaires
Ces zones de transition entre la pleine mer et le fleuve sont des domaines écologiquement riches. Ils sont le lieu de transformation de la marée du fait de 3 principaux paramètres : la pente et la rugosité des fonds et la restriction de gabarit souvent considérée comme exponentielle. Les principaux effets qu'ils produisent sont la diminution de la longueur d'onde, l'augmentation ou la diminution de son amplitude.
Nous nous limitons ici à la propagation de la marée dans un estuaire schématique.
Pour simuler ce phénomène de propagation, nous aurons recours au modèle de Saint-Venant qui permet de simuler l'évolution de la ligne d'eau et des vitesses au cours du temps.
Dans les fiches précédentes (voir ci-dessus), nous avons testé sa résolution en nous limitant aux termes linéaires et avons mis en évidence leur pertinence pour représenter ce qui se passe assez loin de la côte. L'intérêt des résolutions linéaires est de conserver des termes de géométrie qui permettent de prendre en compte l'influence de la pente du fond et celle de la restriction de gabarit qui produisent des gonflements du niveau d'eau et des diminutions de la longueur d'onde.
Cependant, nous pouvons observer dans les estuaires français plusieurs évolutions du signal sinusoïdal à peu près pur en haute mer qui se déforme par raidissement de la face aval de l'hydrogramme en plus des transformations observées ci-dessus.
Nous reprendrons ici le système de résolution du système d'équation de Saint-Venant 1D, mais en conservant le terme non-linéaire d'accélération convective. Cela nous permettra de mettre en évidence son effet sur la déformation du signal.
Nous nous inspirerons de l'article de Le Provost (1) qui présente une résolution des équations de Saint-Venant en comparant solution analytique obtenue par la méthode des caractéristiques et solutions numériques obtenues par divers schémas numériques aux différences finies.
Résolution de l'équation de Saint-Venant 1D par la méthode des caractéristiques
Nous allons donc étudier la propagation d'une onde de marée dans un estuaire à fond plat. Nous supposons ici que l'estuaire est suffisamment large pour ne pas considérer l'influence des parois.
Le système d'équations à résoudre est le système d'équations de Saint-Venant 1D suivant:
$ \dfrac{ \partial h }{ \partial t }+ \dfrac{ \partial }{ \partial x }(H+h)u=0 $
$ \dfrac{ \partial u }{ \partial t }+u \dfrac{ \partial u }{ \partial x }+g \dfrac{ \partial h }{ \partial x }=0 $
Dans lequel, $ u $ est la vitesse, $ H $ la profondeur d'eau moyenne dans le canal, $ h $ le niveau du sommet de l'onde comptée à partir du niveau moyen, $ g $ l'accélération de la gravité, $ S $ la pente du fond.
Nous allons transformer ce système exprimé avec les variables $ (u,h) $ en le système $ (u,c) $ où $ c=\sqrt{g(H+h)} $ est la célérité de propagation de l'onde.
Nous négligerons les variations des fonds au cours du temps. Il vient :
$ \begin{cases} \dfrac{ \partial c^2/g }{ \partial t }+ u\dfrac{ \partial c^2/g }{ \partial x }+ c^2/g\dfrac{ \partial u }{ \partial x }=0 \\ \\ \dfrac{ \partial u }{ \partial t }+u \dfrac{ \partial u }{ \partial x }+g \dfrac{ \partial h }{ \partial x }=-gS \end{cases} $
En réarrangeant le système précédent, nous obtenons:
$ \dfrac{ \partial } { \partial t } (u\pm 2c)+ u\dfrac{ \partial }{ \partial x }(u\pm2c)+ c\dfrac{ \partial }{ \partial x }(u\pm 2c) =-gS $
Soit:
$ \left [\dfrac{ \partial}{ \partial t }+ (u\pm c)\dfrac{ \partial }{ \partial x }\right ](u\pm2c)=-gS $
Si nous considérons la pente du fond comme négligeable, nous obtenons le système suivant:
$ \begin{cases} \dfrac{ d}{ dt }(u\pm 2c) = 0 ==>u\pm2c = Cste \\ \\ \dfrac{ dx}{ dt }=(u\pm c) \end{cases} $
Ainsi, le système peut être représenté par 2 courbes caractéristiques (Cunge (2)) de pentes locales $ C^{ +} : \dfrac{ dx}{ dt }=(u+c) $ et $ C^- : \dfrac{ dx}{ dt }=(u-c) $ le long desquelles les quantités $ u+2c $ et $ u-2c $ se conservent respectivement.
Ainsi, un point $ M $ du plan $ (t,x) $ se trouve à l'intersection de 2 caractéristiques.
Propagation d'une onde dans un canal
Nous nous proposons de résoudre le problème de la propagation d'une onde de marée entrant dans le canal par sa frontière gauche $ x=0 $. Nous imposerons une vitesse $ u $ sinusoïdale à l'entrée du canal.
Les courbes caractéristiques qui correspondent à notre problème sont représentées sur le graphique suivant:
- Remarquons en premier lieu que la caractéristique $ C^{ +} $ (en rouge) qui passe par l'origine correspond à la condition initiale qui est celle du plan d'eau au repos, c'est-à-dire :$ u_0(0,0)=0 $ pas de vitesse imposée à l'instant $ t=0 $. Le long de cette courbe, la quantité $ u+2c =2c_0=\sqrt {gH} $ se conserve, en particulier au point C.
- Exploitons le fait que le point $ M $ se trouve également sur la caractéristique $ C^{ -} $ (courbe verte). A ce titre nous avons la conservation de la quantité : $ u-2c = cste $ en particulier au point C. Ceci nous permet d'écrire:
$ u-2c =-2c_0 $ ou encore $ u=2c-2c_0 $
Nous allons imposer comme condition limite la vitesse $ u_0(t,x=0) $.
Le point $ M $ est à l'intersection des 2 courbes caractéristiques, ce qui nous permet d'écrire:
$ \begin{cases} u+2\sqrt{g(H+h)} = u_0+2\sqrt{gH} \\ u-2\sqrt{g(H+h)} =-2\sqrt{gH} \end{cases} $
En effet, la courbe $ C^- $ rencontre la caractéristique $ C_0^+ $qui provient de 0 et qui représente le niveau du plan d'eau avant l'arrivée de l'onde de marée. Au point $ A $, la vitesse de l'eau est nulle et la célérité est proportionnelle à la profondeur d'eau H.
En additionnant et soustrayant les 2 relations précédentes, nous obtenons le système :
$ (1) \begin{cases} \qquad u=u_0/2 \\ \sqrt{g(H+h)} =u_0/4 +\sqrt{gH} \end{cases} $
Enfin, la pente de la caractéristique $ C^{+} $ (courbe bleue) est donnée par : $ \dfrac{ dx}{ dt }=u+c= 3c-2c_0 $
Olivier Thual (3) a montré que les caractéristiques $ C^{+} $ étaient des droites, ce qui nous permet d'écrire :
$ x=x_0 + (t-t_0)(3c-2c_0) $
En rapprochant l'expression précédente de $ x=x_0 + (t-t_0)(3c-2c_0) $ , nous obtenons:
$ (2) \qquad x=x_0 + (t-t_0)(\dfrac{ 3}{ 4}u_0+\sqrt{gH}) $
Enfin, élevons l'expression reliant les 2 célérités ci-dessus au carré, il vient:
$ (3) \qquad h=\dfrac{1}{ 2}u_0\Big[\dfrac{1}{ 8g} u_0+\sqrt{\dfrac{H}{ g}} \Big] $
Algorithme de résolution
Nous souhaitons connaitre le niveau d'eau en un point quelconque $ M(t,x) $. Utilisons l'expression paramétrique précédente qui relie l'abscisse au temps en utilisant le paramètre $ t=t_0 $.
Connaissant $ x $ et $ t $, résolvons cette équation implicite. Ceci équivaut à aller chercher le pied de la caractéristique en $ x=0 $ qui va être à l'origine de ce qui se passe au point $ M $ à l'instant $ t $ .
Le graphique suivant illustre le comportement de cette fonction implicite.
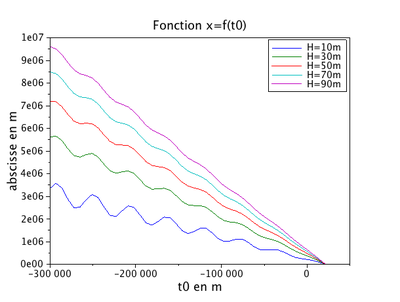
Il apparait que pour les faibles profondeurs, il existe plusieurs valeurs de $ t_0 $ correspondant à une même valeur de $ x $, ce qui empêche de calculer une valeur unique de $ t_0 $. Dans ce cas, nous nous limiterons à prendre des valeurs assez grandes de la profondeur, soit à partir de 70 m dans l'exemple ci-dessus pour laquelle l'oscillation est de moindre intensité.
Exemple numérique
Nous allons choisir comme exemple la propagation d'une onde de marée de période 12h dans un estuaire dont les caractéristiques sont les suivantes:
- longueur : $ 10^7 m $. Cette valeur nous permet de visualiser plusieurs longueurs d'onde dans le même graphique
- pente du fond nulle
- profondeur d'eau au repos : 50 m
ce qui correspond à une longueur d'onde de 1283,629 km
L'animation suivante illustre la propagation d'une telle onde dans notre estuaire fictif
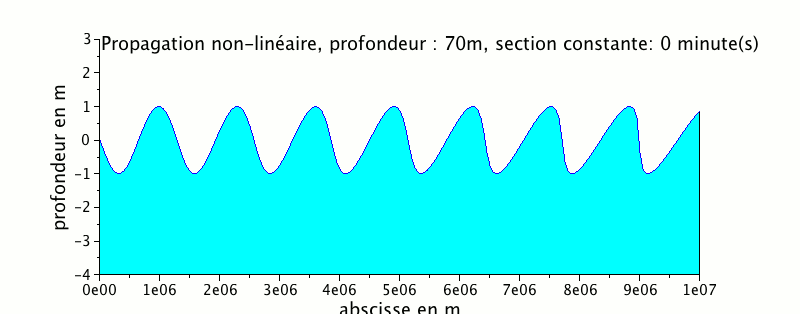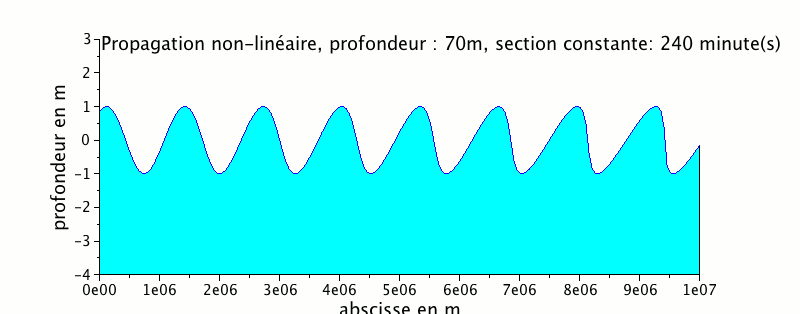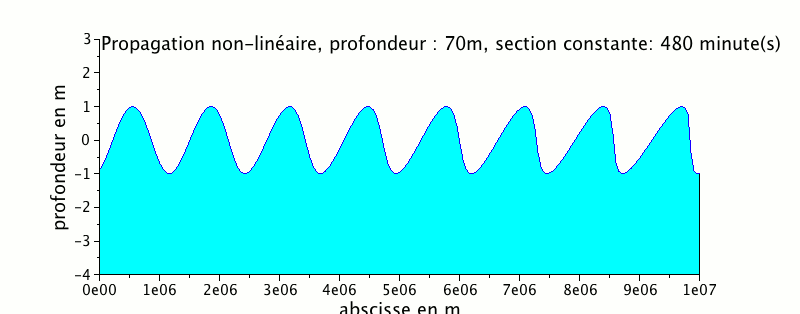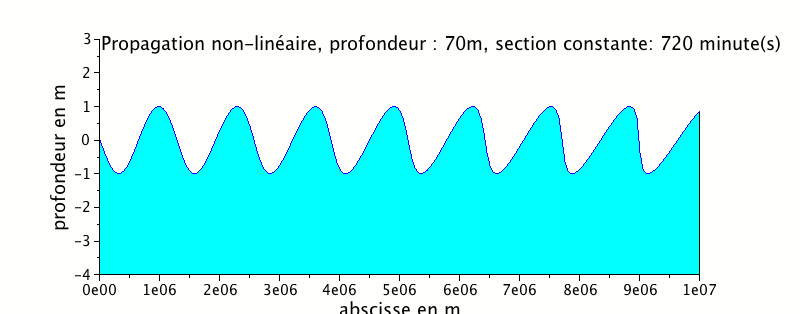
L'animation ci-dessous représente la propagation d'une onde de marée dans un canal de profondeur égale à 70 m
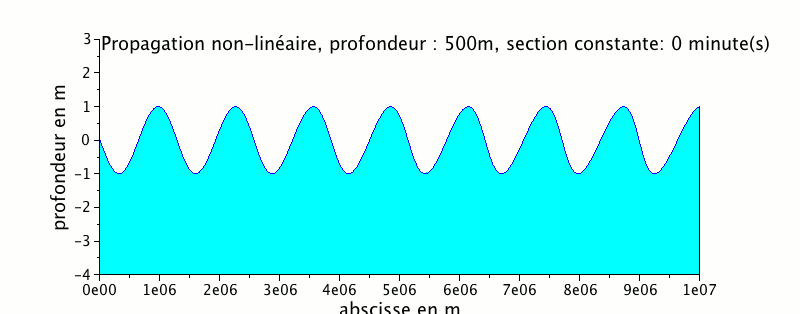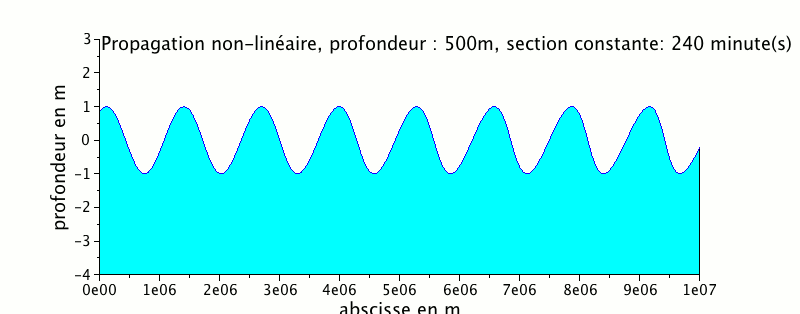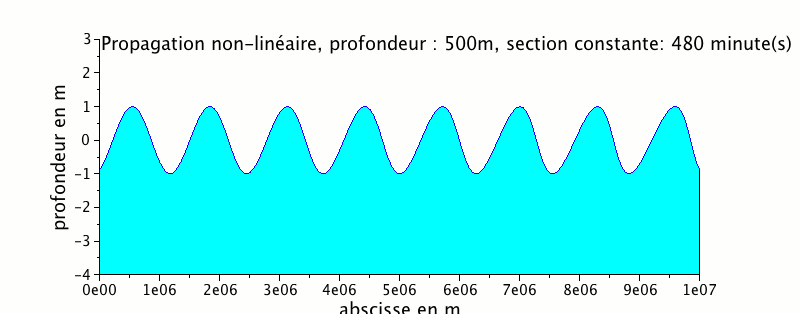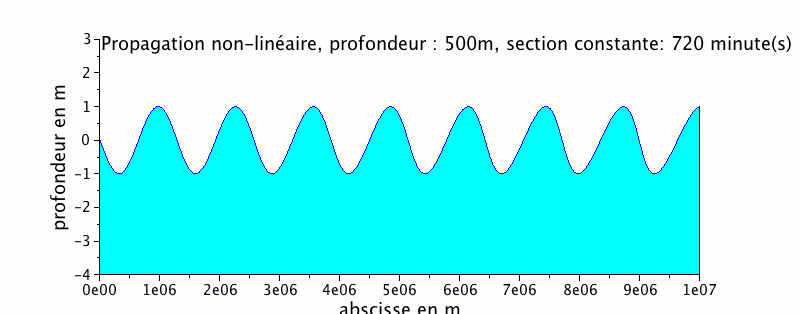
L'animation ci-dessous représente la propagation d'une onde de marée dans un canal de profondeur égale à 500 m
Conclusion
De l'étude ci-dessus, nous pouvons mettre en évidence le rôle très important du terme de convection non-linéaire dans le système d'équations de Saint-Venant. Il produit un raidissement de l'onde de marée sur sa face amont. Ce phénomène n'est pas reproductible par le modèle linéarisé.
On peut remarquer que le signal de marée se cambre beaucoup plus avec une profondeur plus faible.
Bibliographie
- CHristian Le Provost, Océanographie n°9, pp 95 - 113, 1978
- J.A. Cunge, F.M. Holly jr, A. Verwey, "Practical Aspects of Computational River Hydraulics", Pitman Advanced Publishing Program, 420 p, 1980
- 0. Thual, "Hydrodynamique de l'environnement", Les éditions de l'Ecole Polytechnique, Oct. 2011, 314 p.
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS