Calage d'un modèle (HU)

Traduction anglaise : Model Calibration

Dernière mise à jour : 10/04/2024

mot en chantier

Ajustement des valeurs numériques attribuées aux paramètres d'un modèle afin que les valeurs calculées d’une variable ou d’une grandeur soient aussi proches que possible des valeurs observées de cette variable ou de cette grandeur ; on utilise parfois calibration, sans doute en lien avec le mot anglais. Nous traiterons ici exclusivement des modèles hydrologiques et hydrauliques.

Concepts de base

D’une manière générale un modèle $ M $ peut être représenté par une relation fonctionnelle de la forme :

$ M ≡ f [S_j (x, y,t), E_j (x,y,t), {a, b, …. n(x,y,t)}] $

Avec :

$ S_j $ : variables calculées (ou expliquées) par le modèle (par exemple le débit ou le volume dans le cas d'un modèle hydrologique) ;
$ E_j $ : variables de calcul (ou explicantes) ayant un sens physique et mesurables (par exemple la surface du bassin versant ou la hauteur de pluie) ;
$ a, b, … n $ : paramètres d'ajustement.

Il est à noter que, du fait de la complexité des phénomènes en cause, la distinction entre variables de calcul et paramètres est relativement arbitraire. Une même grandeur peut être considéré comme une variable de calcul par un modèle et comme un paramètre par un autre modèle représentant le même phénomène. De plus, suivant la structure du modèle, les valeurs des paramètres peuvent être déduites théoriquement ou empiriquement ou être ajustées numériquement. Par exemple le temps de concentration peut être déduit d'informations mesurables (surface, pente, plus long parcours de l'eau, etc.) ou calé numériquement.

Nous ne traiterons ici que les paramètres de calage dont la valeur est choisie en utilisant une procédure visant à faire correspondre les prévisions du modèle à des observations.

Dans ce sens, le calage est donc une opération de détermination des valeurs numériques des paramètres d’un modèle permettant à ce dernier de « reproduire » un jeu d’événements ou de données observées. Il doit impérativement être suivi d'une autre procédure visant à s'assurer de sa qualité du calage réalisé : l'étape de validation du modèle.

Critères de qualité d'un calage

La qualité du calage peut être appréciée par une fonction d’écart (ou fonction « objectif »), $ E_c $, entre les variables calculées $ S_{jc} $ et observées $ S_{job} $ dont l’expression générale est :

$ E_c = g [S_{jc} (a, b… n) – S_{job}] $

Le choix « optimisé » des paramètres revient à minimiser la fonction d’écart.

Il n’existe pas de fonction d’écart unique pour juger de l’ajustement d’un modèle, en particulier lorsqu’il s’agit d’évaluer sa faculté à reproduire une série chronologique $ S(t) $ (hydrogramme par exemple). Les hydrologues utilisent souvent le critère de Nash-Sutcliffe qui s’écrit ;

$ E_c = 1 – \frac{[ ∑(S_{ob}(i.Δt) – S_c(i.Δt))²]}{[ ∑ (S_{ob} (i.Δt) – S_{mob})² ]} $

Avec :

$ S_{ob} $ et $ S_c $ : Valeurs observées et calculées au i^eme pas de temps ;
$ Δt $ : pas de temps de la série chronologique discrétisée ;
$ S_{mob} $ : moyenne arithmétique des observations.

Ce critère donne beaucoup de poids aux plus fortes valeurs et il est parfois utilisé sur des variables transformées (logarithmes par exemple). D’autres fonctions d’écart peuvent être utilisées ou être appliquées à une fraction seulement des valeurs $ S_{ob} (i.Δt) $ (valeurs maximales ou minimales, valeurs au-dessus d’un seuil, etc.).

Méthode de recherche du calage optimum

Si la fonction objectif est dérivable et que son minimum est unique (fonction convexe), on peut calculer simplement les valeurs optimum des paramètres en résolvant le système d'équations :

$ \frac{∂Ec}{∂a} = \frac{∂Ec}{∂b} = … = \frac{∂Ec}{∂n} = 0 $

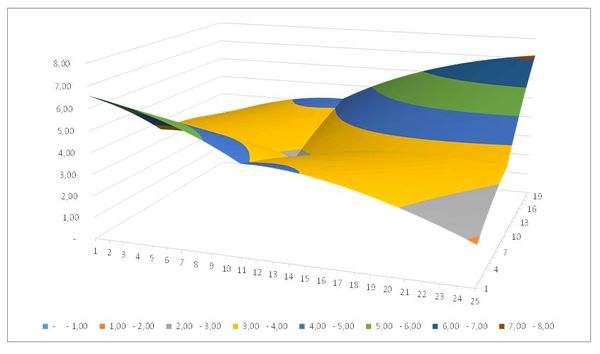
Si ce n'est pas le cas, ce qui est le plus fréquent, le minimum de $ E_c $ peut être également estimé par des techniques de recherche opérationnelle d’exploration numérique de l’hypersurface $ E_c(a, b, …..n) $. Ces méthodes, très variées, sont plus ou moins difficiles à mettre en œuvre en fonction du nombre de paramètres de calage (donc de dimensions de l'espace des solutions), et du caractère plus ou moins explicite de la fonction objectif.

Figure 1 : Exemple de représentation d'une fonction objectif dans un espace à 2 dimensions (2 paramètres de calage) avec plusieurs minimum.

Il arrive d'ailleurs souvent qu'il ne soit pas possible de construire une fonction objectif explicite en fonction des paramètres. La seule possibilité consiste alors à tester différents jeux de paramètres et à retenir celui qui minimise la fonction objectif. Les méthodes d'assimilation des données permettent de trouver des stratégies plus ou moins optimales pour faire varier le jeu de paramètres et converger dans un temps raisonnable vers une "bonne solution" (dont on n'est d'ailleurs jamais vraiment certain qu'elle soit réellement optimale).

Les études de sensibilité sont très utiles pour identifier les paramètres les plus pertinents ainsi que les relations éventuelles (pas toujours simples à détecter) qui existent entre eux.

Les logiciels de simulation incluent de plus en plus souvent des outils de calage semi-automatiques qui facilitent cette étape.

Prise en compte des incertitudes

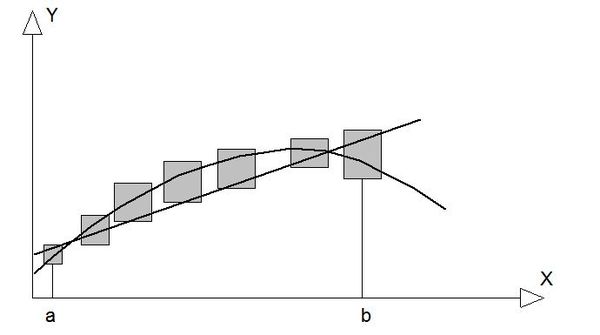
En toute rigueur la fonction d’écart devrait prendre en compte les erreurs et incertitudes des variables $ S_{ob} $ de contrôle mais également celles des variables « explicantes » $ E-j (x,y,t) $ du modèle. Dès lors, on peut aisément concevoir que « l’optimisation » classique des paramètres d’un modèle, sans référence aux erreurs et incertitudes, n’a que peu de chance d’améliorer la connaissance des phénomènes et, notamment, de dégager des valeurs de paramètres applicables à des situations non observées. Certains chercheurs, notamment en hydrologie, ont ainsi développé le concept d’ « équifinalité » des paramètres, dégageant des plages de l’hypersurface $ E_c (a,b,…n) $ de variation des valeurs numériques des paramètres pour lesquelles les performances d’un modèle peuvent être considérées comme équivalentes (Beven, 1996) (figure 2).

Figure 2 : Dans ce cas, si on prend en compte les erreurs et les incertitudes, aucun des deux ajustements ne peut être préféré à l'autre ($ x $ : variable explicante, $ y $ : variable expliquée).

Pour en savoir plus :

Beven, K.J. (1996) : Equifinality and uncertainty in geomorphological modelling ; The scientific nature of Geomorphology (pp. 289-313) ; ed. Wiley ; Chichester ; GB