Classement fréquentiel (HU)
Traduction anglaise : Frequency analysis
Dernière mise à jour : 19/04/2024
Technique d'analyse statistique permettant par exemple de calculer la fréquence d'apparition d'un événement ou celle de dépassement d'un seuil pour une variable aléatoire.
Sommaire |
Méthode de base
Considérons une série de $ P $ valeurs correspondant à des réalisations d'une variable aléatoire $ x $ obtenues sur un échantillon représentatif. Il peut par exemple s'agir des tailles d'un échantillon de $ P $ personnes ou, dans le domaine de l'hydrologie, des débits maximum observés sur un échantillon de $ P $ crues.
L'objectif est de déterminer la fréquence avec laquelle la valeur de la variable dépasse une valeur donnée pour pouvoir en déduire une probabilité de réalisation. On commence donc par affecter à chaque valeur une fréquence empirique de dépassement
Pour ceci, on classe les $ P $ valeurs par ordre décroissant : depuis $ x_1 $ la plus grande, jusqu'à $ x_p $ la plus petite. Considérons la plus grande valeur $ x_1 $. Comme le nombre total de valeurs dans l'échantillon est $ P $, on peut considérer que cette valeur $ x_1 $ est atteinte ou dépassée $ 1 $ fois pour $ P $ réalisations. Sa fréquence empirique de dépassement est donc de $ 1/P $. La valeur classée au deuxième rang, $ x_2 $, est pour sa part atteinte ou dépassée $ 2 $ fois sur le même échantillon. Sa fréquence empirique de dépassement est donc de $ 2/P $. En généralisant ce raisonnement, on pourrait considérer que la valeur $ x_i $, classée au ième rang possède une fréquence empirique de dépassement égale à :
Raffinement de la méthode
Nécessité de compliquer le modèle
En fait, la relation (1) implique que la plus petite valeur de la série (celle ayant le rang $ P $) possède une probabilité d’être dépassée égale à 1
De la même façon, si l’on réalise un classement par ordre croissant la fréquence empirique (de non dépassement cette fois) pour le rang $ i $ devient :
et donc pour la valeur de rang la plus grande (celle de rang $ P $), $ FF_n = 1 $ et donc $ F_n = 0 $, ce qui signifie que cette valeur ne pourrait jamais être dépassée.
Ces deux déductions sont bien évidemment fausses.
Autres formulations possibles
Pour contourner les difficultés résultant de l’emploi des équations (2) et (3), diverses formules de calcul des fréquences empiriques ont pu être proposées, comme, par exemple :
De même, le recours à la théorie de l’échantillonnage, permet de déterminer l’estimation des fréquences empiriques d’échantillons tirés d’une population mère dont la fonction de distribution serait connue :
Ou, encore plus généralement :
Dans ces relations $ α $ et $ β $ dépendent de la nature de la fonction de distribution de la variable que, dans la pratique, on ne connaît pas.
On utilise souvent la relation (5) avec $ α = 0,5 $, (ou, ce qui revient au même, la relation (6) avec $ α = 0,5 $ et $ β = 0 $), qui correspond à une fonction de répartition exponentielle de la variable (modèle de Hazen).
Cas des séries temporelles et passage aux périodes de retour
En hydrologie, ce type de traitement est surtout utilisé pour évaluer les fréquences temporelles d'apparition ou de dépassement d'une valeur caractéristique d'un événement hydrologique. On cherche ainsi à répondre à des questions de la forme : "Combien de crues ont atteint ou dépassé la valeur de débit Qmax au cours du siècle passé ?", ou de façon prédictive : "Combien de fois la valeur de débit Qmax risque-t-elle d'être dépassée au cours du siècle futur ?".
Nota : En pratique on raisonne souvent sur l'inverse de la fréquence temporelle que l'on appelle Période de retour :
Pour ceci il suffit d'associer à l'échantillon une durée d'observation et de calculer les fréquences, non pas par rapport au nombre $ P $ de réalisations dans l'échantillon, mais par rapport à la durée d'observation $ D $.
Précautions d’emplois
Sensibilité au choix de α
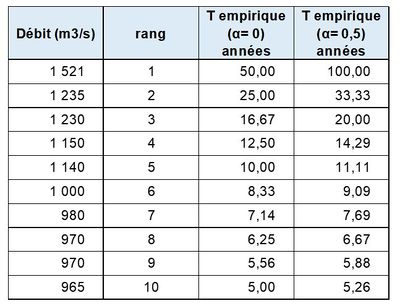
Le calcul de la période de retour empirique est très sensible au choix de $ α $, en particulier pour les rangs les plus faibles. Le tableau de la figure 1 compare par exemple les périodes de retour empiriques obtenues pour différents rangs, pour des valeurs de $ α $ égales à zéro (relation (4) et 0,5 (modèle de Hazen)). Le calcul est fait dans le cas d’un échantillon de 100 observations obtenues au cours d’une durée de 50 ans, soit en moyenne 2 événements par an.
Passage du nombre de valeurs à la durée de la période d’observation
La relation (8) doit être utilisée avec précaution. En effet le nombre de valeurs et la durée d’observation ne correspondent pas aux mêmes grandeurs. En particulier le nombre de valeurs est fixe alors que la durée d'observation dépend de l'unité choisie pour la mesurer (année, mois, jour, etc.). On réduit souvent cette difficulté en ne conservant qu'un évènement par unité de durée d'analyse choisie (par exemple l'évènement annuel le plus fort). Cette approche conduit cependant à ne pas prendre en compte certains évènements marquants (il est par exemple parfaitement possible que les deux crues les plus fortes d'un siècle donné aient lieu la même année tout en étant indépendantes).
De plus la durée d'observation à retenir n'est égale à la durée pendant laquelle les données ont été recueillies que si l'échantillon est complet, c'est à dire si tous les événements significatifs ont effectivement été enregistrés. Or il arrive souvent en hydrologie que les séries de données soient lacunaires (généralement du fait de pannes du capteur). Dans ce cas la durée réelle d'observation doit être réduite, à moins que l'on fasse le choix de compléter artificiellement la série (par exemple, dans le cas de la panne d'un pluviomètre, en utilisant sur la période manquante les données d'un pluviomètre voisin).
Ajustement des fréquences empiriques
Une fois les fréquences empiriques calculées le passage des statistiques aux probabilités nécessite la construction d'une relation analytique permettant de lisser les valeurs.
Ce lissage peut se faire de façon totalement empirique en choisissant une fonction d'approximation et en utilisant par exemple la méthode des moindres carrés. Cependant on préfère souvent postuler a priori une loi de distribution statistique des valeurs. Cette distribution statistique est souvent choisie pour bien représenter les valeurs les plus fortes. Les distributions correspondantes sont fortement dissymétriques et, en hydrologie, les valeurs extrêmes correspondant à de grandes périodes de retour sont le plus souvent ajustées par des modèles exponentiels (lois de valeurs extrêmes).
Le modèle le plus classique est le modèle de Gumbel qui ajuste la relation entre la fréquence $ F(x) $ et la variable hydrologique $ x $ par une relation de la forme :
Cette relation peut facilement être linéarisée :
En posant :
On obtient une relation linéaire :
qui permet de calculer facilement les valeurs de $ a $ et $ b $ en ajustant au mieux les valeurs empiriques de $ X_i== -ln(-ln(F(x_i))) $ et $ Y_i=x_i $.
Précautions d'emploi
Cette méthode, malgré sa simplicité, doit être utilisée avec précautions. Différents biais sont en effet possibles.
L'échantillon est-il représentatif de la population étudiée ?
Le premier biais porte sur l'homogénéité de la population étudiée et la représentativité de l'échantillon. Imaginons par exemple que l'on s'intéresse au poids maximum que peut atteindre un animal. Tout se passe bien si l'échantillon comprend uniquement des cochons et si c'est la probabilité que ce type d'animal dépasse un certain poids qui nous intéresse. Mais si, avec le même échantillon composé uniquement de cochons, on s'intéresse au poids maximum que peut atteindre un animal de ferme, on sera très surpris lorsque l'on pèsera un bœuf. En matière d'hydrologie, ce risque est très présent. Les phénomènes générateurs des précipitations sont en effet divers et leurs conséquences hydrologiques peuvent être très différentes. Analyser uniquement une variable aléatoire (par exemple le débit maximum de crue), sans se préoccuper de la nature des phénomènes générateurs fait courir le risque de mélanger des populations d'événements différentes dont la fréquence relative peut changer dans le temps (voir le § "Le futur sera-t-il semblable au passé ?").
La durée d'observation est-elle suffisante ?
Un autre biais possible concerne la durée d'observation relativement à la période de retour d'intérêt. Les durées d'observations sont en effet souvent relativement courtes (on ne dispose par exemple, sauf exception, de séries pluviométriques à des pas de temps courts que depuis une cinquantaine d'années) et les phénomènes hydrologiques importants se manifestent de façon extrêmement irrégulière. Il est par exemple parfaitement possible d'observer deux crues de période de retour 10 ans dans la même année et de rester ensuite plusieurs dizaines d'années sans en observer une nouvelle. De ce fait on peut considérer qu'une durée d'observation de $ T $ années permet d'estimer correctement le risque de dépassement d'une valeur pour une période de retour de $ T/3 $ années au maximum. En aucun cas cette durée d'observation ne permet d'estimer le risque pour une période de retour supérieure à la durée d'observation.
Nota : Moyennant certaines conditions, il existe des méthodes permettant de dépasser la durée de la période d'observation : voir Année station (méthode des) et Gradex (méthode du)
Le futur sera-t-il semblable au passé ?
Une hypothèse extrêmement forte est nécessaire pour passer des statistiques (qui utilisent les données du passé) aux probabilités (que l'on souhaite utiliser pour estimer les risques futurs) : la stabilité des phénomènes dans le temps. En d'autres termes, cette approche n'a de sens que si le futur est semblable au passé. Or les conséquences du changement climatique en matière d'hydrologie rendent cette hypothèse très peu probable.
De plus les évolutions risquent d'être catastrophiques (au sens de la théorie des catastrophes de Thom), c'est à dire ne pas se caractériser par une évolution régulière mais par des "bifurcations". Par exemple, il est possible d'observer en France une remontée vers le Nord des phénomènes pluvieux que l'on observe actuellement uniquement près de la Méditerranée. Ceci rejoint le premier point évoqué : les pluies maximum que l'on pourra alors observer dans les zones concernées ne correspondront pas à la population sur laquelle on a établi les statistiques. Elles ne peuvent donc pas être estimées par cette méthode, de la même façon que des statistiques sur le poids des cochons ne permettent pas de prévoir le poids possible d'un bœuf.
Si la technique du classement fréquentiel est facile et extrêmement utile, il est donc cependant très important de toujours garder un regard critique sur les enseignements que nous pouvons en tirer.
 S'abonner à un flux RSS
S'abonner à un flux RSS