C.06 - Approches bayésiennes : Différence entre versions
(→Relation de Bayes) |
|||
| (Une révision intermédiaire par un utilisateur est masquée) | |||
| Ligne 5 : | Ligne 5 : | ||
== Principe == | == Principe == | ||
| − | Au lieu d'acquérir une connaissance de l'incertitude sur la base d'un ensemble de prévisions passées (fiche | + | Au lieu d'acquérir une connaissance de l'incertitude sur la base d'un ensemble de prévisions passées ([[C.07_-_Apprentissage_:_analyse_a_posteriori_des_erreurs_de_prévision|fiche C.07]]), les approches bayésiennes proposent de faire évoluer notre estimation de l'incertitude dès qu'une nouvelle information est disponible, c'est-à-dire pour nous prévisionnistes, dès qu'une nouvelle observation arrive, qui peut être mise en regard avec les prévisions faites pour cet événement. |
| − | Ces approches se fondent sur le théorème de Bayes qui décrit comment transformer notre connaissance avant l'apport d'information contenue par une observation en une connaissance enrichie tenant compte de cette information. Chaque nouvelle information est elle-même évaluée à partir de notre connaissance du fonctionnement du système étudié | + | Ces approches se fondent sur le théorème de Bayes qui décrit comment transformer notre connaissance avant l'apport d'information contenue par une observation en une connaissance enrichie tenant compte de cette information. Chaque nouvelle information est elle-même évaluée à partir de notre connaissance du fonctionnement du système étudié<ref>Il s'agit ici de notre connaissance du bassin versant ou du réseau hydrographique que nous avons transcrite dans un modèle qui peut être validé (totalement ou partiellement) mais reste en tout état de cause un ensemble d'hypothèses de travail.</ref> (ou de nos hypothèses sur ce système). |
== Formalisme == | == Formalisme == | ||
| Ligne 15 : | Ligne 15 : | ||
Les approches bayésiennes décrivent notre connaissance de l'incertitude par des densités de probabilité. Nos connaissances sur le système étudié sont exprimées par la vraisemblance des données, qui est la densité décrivant la probabilité d'une observation Xt = x, étant donnée notre connaissance du système (notre modèle). | Les approches bayésiennes décrivent notre connaissance de l'incertitude par des densités de probabilité. Nos connaissances sur le système étudié sont exprimées par la vraisemblance des données, qui est la densité décrivant la probabilité d'une observation Xt = x, étant donnée notre connaissance du système (notre modèle). | ||
| − | Le théorème de Bayes | + | Le théorème de Bayes<ref>Bayes était un mathématicien anglais de la première partie du XVIIIe siècle.</ref> décrit une relation entre probabilités conditionnelles (P(A|B)): la probabilité de A sachant B est la probabilité d'un événement A étant donné une information B, [[A.08_-_Probabilités|fiche A.08]]). Cette relation<ref>Ce théorème vient du fait que [[File:Inc247.bmp|250px]]</ref> s'écrit : |
<center> | <center> | ||
| Ligne 28 : | Ligne 28 : | ||
* P(A) est l'estimation initiale de l'incertitude sur la variable à prévoir X : Px(X) | * P(A) est l'estimation initiale de l'incertitude sur la variable à prévoir X : Px(X) | ||
* P(A|B) est alors l'estimation après prise en compte de l'information B (qui sera pour nous une observation Obs de débit ou de hauteur): Px(X|Obs) | * P(A|B) est alors l'estimation après prise en compte de l'information B (qui sera pour nous une observation Obs de débit ou de hauteur): Px(X|Obs) | ||
| − | * P(B|A) est la vraisemblance [ | + | * P(B|A) est la vraisemblance<ref>Vraisemblance se dit likelihood en anglais, ce qui explique qu'elle soit souvent notée par la lettre [[File:Inc248.bmp|20px]].</ref> de l'information B étant donné notre connaissance (le modèle M): [[File:Inc245.bmp|100px]] |
| Ligne 39 : | Ligne 39 : | ||
| − | où le symbole [[File:Inc249.bmp|20px]] indique la proportionnalité [ | + | où le symbole [[File:Inc249.bmp|20px]] indique la proportionnalité<ref>Il n'est pas nécessaire de calculer le dénominateur de l'équation 1 dans la mesure où les probabilités sont « normées » (elles sont comprises entre 0 (fait impossible) et 1 (fait certain), cf. [[A.08_-_Probabilités|fiche A.08]]). Aussi l'équation 1 est ramenée à [[File:Inc258.bmp|170px]] (où le symbole indique la proportionnalité).</ref>. |
| Ligne 62 : | Ligne 62 : | ||
== Applications pratiques == | == Applications pratiques == | ||
| − | Comme dans le cas de la propagation des incertitudes (fiche | + | Comme dans le cas de la propagation des incertitudes ([[C.05_-_Approches_stochastiques_(méthodes_de_Monte-Carlo)|fiche C.05]]), il est très difficile ou impossible de résoudre analytiquement l'équation 2 (c'est-à-dire de fournir une expression analytique de l'incertitude de prévision a posteriori). Les implémentations pratiques sont donc réalisées par une démarche stochastique ([[C.05_-_Approches_stochastiques_(méthodes_de_Monte-Carlo)|fiche C.05]]). Les exemples suivants décrivent des méthodes souvent implémentées en hydrologie ou en hydraulique. |
| − | '''Exemple 2 : GLUE.''' La méthode GLUE | + | '''Exemple 2 : GLUE.''' La méthode GLUE<ref>Generalized Linear Uncertainty Estimation.</ref>, proposée initialement par Beven et Binley (1992), a connu un très grand succès en hydrologie (de nombreuses applications ont été tentées). Son principe est de tirer aléatoirement un très grand nombre de jeu de paramètres (du modèle hydrologique) et d'évaluer leur performance sur des événements passés à l'aide d'une vraisemblance informelle (qui n'est ni plus ni moins qu'un critère de performance). Seuls sont sélectionnés les jeux de paramètres qui obtiennent une valeur de cette vraisemblance informelle supérieure à un seuil choisi. La distribution des prévisions correspond alors à l'ensemble des prévisions obtenues avec les jeux de paramètres conservés, pondérées par la valeur de vraisemblance (informelle). Le théorème de Bayes permet dans ce cadre de faire évoluer cette distribution à mesure que de nouvelles observations sont disponibles. Cette approche a été au cœur d'une controverse assez intense, portant notamment sur son caractère informel qui ne correspond pas au cadre bayésien rigoureux. En pratique, la méthode ne s'intéresse qu'à l'incertitude des paramètres, ce qui conduit dans la très grande majorité des cas à une sous-estimation significative des incertitudes de prévision. |
| − | '''Exemple 3 : filtre particulaire.''' L'état à un instant t d'un système physique (comme un bassin versant ou un réseau hydrographique) représenté par un modèle déterministe est décrit par les valeurs des n états [[File:Inc252.bmp|35px]] du modèle et de ses m paramètres [[File:Inc254.bmp|35px]] qu'on peut rassembler dans [[File:Inc253.bmp|250px]]. Si on tient compte de sources d'incertitude, alors les états du modèle ne sont plus connus de façon déterministe et doivent être décrits par leur densité de probabilité jointe | + | '''Exemple 3 : filtre particulaire.''' L'état à un instant t d'un système physique (comme un bassin versant ou un réseau hydrographique) représenté par un modèle déterministe est décrit par les valeurs des n états [[File:Inc252.bmp|35px]] du modèle et de ses m paramètres [[File:Inc254.bmp|35px]] qu'on peut rassembler dans [[File:Inc253.bmp|250px]]. Si on tient compte de sources d'incertitude, alors les états du modèle ne sont plus connus de façon déterministe et doivent être décrits par leur densité de probabilité jointe<ref>C'est également vrai pour les paramètres si on prend en compte une incertitude sur eux.</ref>. Dans la mise en œuvre du filtre particulaire, cette densité jointe est décrite par un ensemble de vecteurs [[File:Inc255.bmp|200px]], qu'on appelle des particules. Chaque particule [[File:Inc256.bmp|45px]] représente un état possible du système étudié à l'instant t et on lui associe un poids wi qui rend compte de sa probabilité. Pour passer d'un pas de temps au suivant, le modèle est exécuté avec chaque particule [[File:Inc256.bmp|45px]] pour obtenir la particule [[File:Inc257.bmp|60px]] ; les sources d'incertitude sont prises en compte en prenant une réalisation possible des variables aléatoires associées dans l'exécution du modèle. À chaque nouvelle observation, le théorème de Bayes est employé pour mettre à jour les poids des particules. Ainsi, la densité de probabilité de la variable à prévoir est donnée par la distribution des sorties de chaque particule pondérées de leurs poids respectifs. Le lecteur intéressé par plus de détails pourra se référer entre autres à Weerts et Serafy (2006). |
| − | '''Exemple 4 : Bayesian Total Error Analysis (BATEA).''' Cette approche vise à une description explicite de l'ensemble des sources d'incertitude d'un modèle hydrologique qui sont combinées par l'approche bayésienne pour donner l'incertitude de prévision. L'implémentation emploie des algorithmes de simulation MCMC | + | '''Exemple 4 : Bayesian Total Error Analysis (BATEA).''' Cette approche vise à une description explicite de l'ensemble des sources d'incertitude d'un modèle hydrologique qui sont combinées par l'approche bayésienne pour donner l'incertitude de prévision. L'implémentation emploie des algorithmes de simulation MCMC<ref>Algorithme Markov Chain Monte-Carlo.</ref> pour échantillonner ces densités de probabilité. Le lecteur intéressé par plus de détails pourra se référer à Kavetski et al. (2006). Cette approche est plus adaptée à la simulation qu'à la prévision (elle est rarement implémentée en mode séquentiel, permettant une mise à jour de la description de l'incertitude de prévision). |
'''Exemple 5 : Bayesian Model Averaging (BMA).''' Il s'agit d'une méthode permettant de combiner des prévisions de plusieurs modèles (probabilistes) en les pondérant. Le théorème de Bayes permet de faire évoluer les poids des différents modèles en fonction de leurs performances au vu des observations qui deviennent disponibles. Le lecteur intéressé par plus de détails pourra se référer à Hoeting et al. (1999). | '''Exemple 5 : Bayesian Model Averaging (BMA).''' Il s'agit d'une méthode permettant de combiner des prévisions de plusieurs modèles (probabilistes) en les pondérant. Le théorème de Bayes permet de faire évoluer les poids des différents modèles en fonction de leurs performances au vu des observations qui deviennent disponibles. Le lecteur intéressé par plus de détails pourra se référer à Hoeting et al. (1999). | ||
| Ligne 84 : | Ligne 84 : | ||
=== Choix du prior initial === | === Choix du prior initial === | ||
| − | Un débat sans cesse renouvelé parmi les statisticiens, partisans pour les uns des approches fréquentistes, pour les autres des approches bayésiennes (fiche | + | Un débat sans cesse renouvelé parmi les statisticiens, partisans pour les uns des approches fréquentistes, pour les autres des approches bayésiennes ([[A.08_-_Probabilités|fiche A.08]]), concernent le choix du prior initial<ref>Il s'agit de la description de l'incertitude faite avant tout emploi du théorème de Bayes, c'est-à-dire de toute prise en compte d'observations nouvelles.</ref>. Ce dernier est à exprimer par le modélisateur ou le prévisionniste : il traduit son expertise de l'incertitude en dehors de tout apprentissage (par les observations). Il s'agit donc d'un choix subjectif, souvent critiqué. Ce choix doit être considéré comme une des hypothèses employées et peut donc être remise en cause. |
Quand on ne veut pas « apporter » d'information particulière dans le choix du prior, il est fréquent d'opter pour une distribution uniforme entre deux bornes. Cela revient à dire que la variable X peut prendre n'importe quelle valeur (entre ces bornes) de façon équiprobable. Il est toutefois nécessaire de bien choisir la variable (par exemple : débit ou hauteur) sur laquelle faire cette hypothèse : en effet, comme la courbe de tarage n'est pas linéaire, choisir une distribution a priori des hauteurs uniforme implique de supposer que celle des débits ne l'est pas... | Quand on ne veut pas « apporter » d'information particulière dans le choix du prior, il est fréquent d'opter pour une distribution uniforme entre deux bornes. Cela revient à dire que la variable X peut prendre n'importe quelle valeur (entre ces bornes) de façon équiprobable. Il est toutefois nécessaire de bien choisir la variable (par exemple : débit ou hauteur) sur laquelle faire cette hypothèse : en effet, comme la courbe de tarage n'est pas linéaire, choisir une distribution a priori des hauteurs uniforme implique de supposer que celle des débits ne l'est pas... | ||
| Ligne 91 : | Ligne 91 : | ||
Adjoindre un modèle d'erreur à un modèle hydraulique ou hydrologique déterministe n'est pas une tâche très aisée. Il est impératif de contrôler ce modèle d'erreur. En hydrologie au moins, il est très rare de valider complètement un modèle d'erreur. | Adjoindre un modèle d'erreur à un modèle hydraulique ou hydrologique déterministe n'est pas une tâche très aisée. Il est impératif de contrôler ce modèle d'erreur. En hydrologie au moins, il est très rare de valider complètement un modèle d'erreur. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''Voir également''' | '''Voir également''' | ||
| − | Fiche | + | [[A.08_-_Probabilités|Fiche A.08 – Probabilités]] |
| − | Fiche | + | [[C.05_-_Approches_stochastiques_(méthodes_de_Monte-Carlo)|Fiche C.05 – Approches stochastiques]] |
| − | Fiche | + | [[C.07_-_Apprentissage_:_analyse_a_posteriori_des_erreurs_de_prévision|Fiche C.07 – Apprentissage par analyse a posteriori des erreurs de prévision]] |
| Ligne 135 : | Ligne 111 : | ||
* http://udsmed.u-strasbg.fr/labiostat/IMG/pdf/Nicolas_MEYER_BMA.pdf | * http://udsmed.u-strasbg.fr/labiostat/IMG/pdf/Nicolas_MEYER_BMA.pdf | ||
| + | |||
| + | ----------------- | ||
| + | <references> | ||
[[Catégorie:Incertitudes]] | [[Catégorie:Incertitudes]] | ||
Version actuelle en date du 24 janvier 2015 à 23:19
Sommaire |
[modifier] Introduction
Cette fiche vise seulement à introduire le principe des approches bayésiennes, à expliciter la terminologie usuelle qui leur est propre et à indiquer certains points-clefs et difficultés. Il est impossible en quelques pages de décrire en détails l'ensemble de ces méthodes et de leurs emplois dans le domaine de la prévision.
[modifier] Principe
Au lieu d'acquérir une connaissance de l'incertitude sur la base d'un ensemble de prévisions passées (fiche C.07), les approches bayésiennes proposent de faire évoluer notre estimation de l'incertitude dès qu'une nouvelle information est disponible, c'est-à-dire pour nous prévisionnistes, dès qu'une nouvelle observation arrive, qui peut être mise en regard avec les prévisions faites pour cet événement.
Ces approches se fondent sur le théorème de Bayes qui décrit comment transformer notre connaissance avant l'apport d'information contenue par une observation en une connaissance enrichie tenant compte de cette information. Chaque nouvelle information est elle-même évaluée à partir de notre connaissance du fonctionnement du système étudié[1] (ou de nos hypothèses sur ce système).
[modifier] Formalisme
[modifier] Relation de Bayes
Les approches bayésiennes décrivent notre connaissance de l'incertitude par des densités de probabilité. Nos connaissances sur le système étudié sont exprimées par la vraisemblance des données, qui est la densité décrivant la probabilité d'une observation Xt = x, étant donnée notre connaissance du système (notre modèle).
Le théorème de Bayes[2] décrit une relation entre probabilités conditionnelles (P(A|B)): la probabilité de A sachant B est la probabilité d'un événement A étant donné une information B, fiche A.08). Cette relation[3] s'écrit :
Ce théorème simple permet donc l'estimation de l'incertitude après prise en compte de la nouvelle observation B, appelée distribution a posteriori, ou encore posterior (P(A|B)), à partir de son estimation avant prise en compte, appelée distribution a priori ou prior (P(A))et la vraisemblance de l'observation B en question (probabilité de B connaissant A : P(B|A).
Dans le cadre d'un système de prévision :
- P(A) est l'estimation initiale de l'incertitude sur la variable à prévoir X : Px(X)
- P(A|B) est alors l'estimation après prise en compte de l'information B (qui sera pour nous une observation Obs de débit ou de hauteur): Px(X|Obs)
- P(B|A) est la vraisemblance[4] de l'information B étant donné notre connaissance (le modèle M):
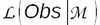
L'équation 1. peut donc être réécrite en :
où le symbole ![]() indique la proportionnalité[5].
indique la proportionnalité[5].
L’équation précédente peut alors être appliquée de façon itérative. L’apport de la ![]() observation est alors donné par :
observation est alors donné par :
[modifier] Explicitation de la vraisemblance
La vraisemblance d'une ou des observations correspond à la valeur de la densité de probabilité de cette ou ces observations, étant donné le modèle (qui traduit notre compréhension du système). Son emploi suppose que notre description du système n'est pas déterministe.
Le modèle peut être probabiliste, c'est-à-dire qu'il ne fournit pas une prévision déterministe mais une densité de probabilité du débit ou de la hauteur prévue.
Un modèle déterministe peut toutefois être « adapté » en lui adjoignant un modèle d'erreur qui décrit la densité de probabilité de l'erreur par rapport à la prévision déterministe.
Exemple 1. Une hypothèse souvent faite est celle d'un modèle d'erreur défini comme étant une loi de probabilité normale de moyenne nulle (on suppose que le modèle déterministe est non biaisé) et d'écart-type donné. Malheureusement, ce modèle d'erreur est le plus souvent peu adapté aux modèles hydrologiques de prévision. Une densité de probabilité non symétrique est souvent préférable, de même qu'une description « hétéroscédastique » (la variabilité de l'erreur augmente avec la prévision de débit).
[modifier] Applications pratiques
Comme dans le cas de la propagation des incertitudes (fiche C.05), il est très difficile ou impossible de résoudre analytiquement l'équation 2 (c'est-à-dire de fournir une expression analytique de l'incertitude de prévision a posteriori). Les implémentations pratiques sont donc réalisées par une démarche stochastique (fiche C.05). Les exemples suivants décrivent des méthodes souvent implémentées en hydrologie ou en hydraulique.
Exemple 2 : GLUE. La méthode GLUE[6], proposée initialement par Beven et Binley (1992), a connu un très grand succès en hydrologie (de nombreuses applications ont été tentées). Son principe est de tirer aléatoirement un très grand nombre de jeu de paramètres (du modèle hydrologique) et d'évaluer leur performance sur des événements passés à l'aide d'une vraisemblance informelle (qui n'est ni plus ni moins qu'un critère de performance). Seuls sont sélectionnés les jeux de paramètres qui obtiennent une valeur de cette vraisemblance informelle supérieure à un seuil choisi. La distribution des prévisions correspond alors à l'ensemble des prévisions obtenues avec les jeux de paramètres conservés, pondérées par la valeur de vraisemblance (informelle). Le théorème de Bayes permet dans ce cadre de faire évoluer cette distribution à mesure que de nouvelles observations sont disponibles. Cette approche a été au cœur d'une controverse assez intense, portant notamment sur son caractère informel qui ne correspond pas au cadre bayésien rigoureux. En pratique, la méthode ne s'intéresse qu'à l'incertitude des paramètres, ce qui conduit dans la très grande majorité des cas à une sous-estimation significative des incertitudes de prévision.
Exemple 3 : filtre particulaire. L'état à un instant t d'un système physique (comme un bassin versant ou un réseau hydrographique) représenté par un modèle déterministe est décrit par les valeurs des n états ![]() du modèle et de ses m paramètres
du modèle et de ses m paramètres ![]() qu'on peut rassembler dans
qu'on peut rassembler dans ![]() . Si on tient compte de sources d'incertitude, alors les états du modèle ne sont plus connus de façon déterministe et doivent être décrits par leur densité de probabilité jointe[7]. Dans la mise en œuvre du filtre particulaire, cette densité jointe est décrite par un ensemble de vecteurs
. Si on tient compte de sources d'incertitude, alors les états du modèle ne sont plus connus de façon déterministe et doivent être décrits par leur densité de probabilité jointe[7]. Dans la mise en œuvre du filtre particulaire, cette densité jointe est décrite par un ensemble de vecteurs ![]() , qu'on appelle des particules. Chaque particule
, qu'on appelle des particules. Chaque particule ![]() représente un état possible du système étudié à l'instant t et on lui associe un poids wi qui rend compte de sa probabilité. Pour passer d'un pas de temps au suivant, le modèle est exécuté avec chaque particule
représente un état possible du système étudié à l'instant t et on lui associe un poids wi qui rend compte de sa probabilité. Pour passer d'un pas de temps au suivant, le modèle est exécuté avec chaque particule ![]() pour obtenir la particule
pour obtenir la particule ![]() ; les sources d'incertitude sont prises en compte en prenant une réalisation possible des variables aléatoires associées dans l'exécution du modèle. À chaque nouvelle observation, le théorème de Bayes est employé pour mettre à jour les poids des particules. Ainsi, la densité de probabilité de la variable à prévoir est donnée par la distribution des sorties de chaque particule pondérées de leurs poids respectifs. Le lecteur intéressé par plus de détails pourra se référer entre autres à Weerts et Serafy (2006).
; les sources d'incertitude sont prises en compte en prenant une réalisation possible des variables aléatoires associées dans l'exécution du modèle. À chaque nouvelle observation, le théorème de Bayes est employé pour mettre à jour les poids des particules. Ainsi, la densité de probabilité de la variable à prévoir est donnée par la distribution des sorties de chaque particule pondérées de leurs poids respectifs. Le lecteur intéressé par plus de détails pourra se référer entre autres à Weerts et Serafy (2006).
Exemple 4 : Bayesian Total Error Analysis (BATEA). Cette approche vise à une description explicite de l'ensemble des sources d'incertitude d'un modèle hydrologique qui sont combinées par l'approche bayésienne pour donner l'incertitude de prévision. L'implémentation emploie des algorithmes de simulation MCMC[8] pour échantillonner ces densités de probabilité. Le lecteur intéressé par plus de détails pourra se référer à Kavetski et al. (2006). Cette approche est plus adaptée à la simulation qu'à la prévision (elle est rarement implémentée en mode séquentiel, permettant une mise à jour de la description de l'incertitude de prévision).
Exemple 5 : Bayesian Model Averaging (BMA). Il s'agit d'une méthode permettant de combiner des prévisions de plusieurs modèles (probabilistes) en les pondérant. Le théorème de Bayes permet de faire évoluer les poids des différents modèles en fonction de leurs performances au vu des observations qui deviennent disponibles. Le lecteur intéressé par plus de détails pourra se référer à Hoeting et al. (1999).
[modifier] Points sensibles
[modifier] Description du modèle probabiliste
Comme pour les autres méthodes, l'un des points les plus sensibles reste le choix des sources d'incertitude à quantifier puis leur description : opter pour ce type de méthodes ne résout pas les difficultés « génériques » de l'estimation des incertitudes de prévision.
[modifier] Interaction entre les différentes sources d'incertitude
Là encore, comme pour d'autres méthodes, les interactions entre sources d'incertitude peuvent rendre l'implémentation particulièrement délicate. Le choix des sources d'incertitude à prendre en compte est donc important.
[modifier] Choix du prior initial
Un débat sans cesse renouvelé parmi les statisticiens, partisans pour les uns des approches fréquentistes, pour les autres des approches bayésiennes (fiche A.08), concernent le choix du prior initial[9]. Ce dernier est à exprimer par le modélisateur ou le prévisionniste : il traduit son expertise de l'incertitude en dehors de tout apprentissage (par les observations). Il s'agit donc d'un choix subjectif, souvent critiqué. Ce choix doit être considéré comme une des hypothèses employées et peut donc être remise en cause.
Quand on ne veut pas « apporter » d'information particulière dans le choix du prior, il est fréquent d'opter pour une distribution uniforme entre deux bornes. Cela revient à dire que la variable X peut prendre n'importe quelle valeur (entre ces bornes) de façon équiprobable. Il est toutefois nécessaire de bien choisir la variable (par exemple : débit ou hauteur) sur laquelle faire cette hypothèse : en effet, comme la courbe de tarage n'est pas linéaire, choisir une distribution a priori des hauteurs uniforme implique de supposer que celle des débits ne l'est pas...
[modifier] Expression de la vraisemblance
Adjoindre un modèle d'erreur à un modèle hydraulique ou hydrologique déterministe n'est pas une tâche très aisée. Il est impératif de contrôler ce modèle d'erreur. En hydrologie au moins, il est très rare de valider complètement un modèle d'erreur.
Voir également
Fiche C.05 – Approches stochastiques
Fiche C.07 – Apprentissage par analyse a posteriori des erreurs de prévision
Pour aller plus loin
- Beven, K. J. et Binley, A. M. (1992). The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Processes, 6, 279– 298. doi:10.1002/hyp.3360060305
- Hoeting, J. A., Madigan, D., Raftery A. E. et Volinsky, C. T. (1999). Bayesian Model Averaging: A Tutorial. Statistical Science. 14 (4), 382 – 417.
http://www.iipl.fudan.edu.cn/~zhangjp/literatures/cluster%20analysis/hoeting.pdf
- Kavetski, D., Kuczera, G. et Franks, S. W. (2006). Bayesian analysis of input uncertainty in hydrological modeling: 2. Application. Water Resources Research, 42, W03408. doi:10.1029/2005WR004376.
- Weerts, A. et El Serafy, G. (2006). Particle filtering and ensemble Kalman filtering for state updating with hydrological conceptual rainfall-runo models. Water Resources Research, 42(9), W09403.
- http://udsmed.u-strasbg.fr/labiostat/IMG/pdf/Nicolas_MEYER_BMA.pdf
- ↑ Il s'agit ici de notre connaissance du bassin versant ou du réseau hydrographique que nous avons transcrite dans un modèle qui peut être validé (totalement ou partiellement) mais reste en tout état de cause un ensemble d'hypothèses de travail.
- ↑ Bayes était un mathématicien anglais de la première partie du XVIIIe siècle.
- ↑ Ce théorème vient du fait que

- ↑ Vraisemblance se dit likelihood en anglais, ce qui explique qu'elle soit souvent notée par la lettre
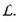 .
.
- ↑ Il n'est pas nécessaire de calculer le dénominateur de l'équation 1 dans la mesure où les probabilités sont « normées » (elles sont comprises entre 0 (fait impossible) et 1 (fait certain), cf. fiche A.08). Aussi l'équation 1 est ramenée à
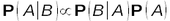 (où le symbole indique la proportionnalité).
(où le symbole indique la proportionnalité).
- ↑ Generalized Linear Uncertainty Estimation.
- ↑ C'est également vrai pour les paramètres si on prend en compte une incertitude sur eux.
- ↑ Algorithme Markov Chain Monte-Carlo.
- ↑ Il s'agit de la description de l'incertitude faite avant tout emploi du théorème de Bayes, c'est-à-dire de toute prise en compte d'observations nouvelles.
 S'abonner à un flux RSS
S'abonner à un flux RSS