Durée en eau (HU) : Différence entre versions
(→Différents choix possibles) |
(→Différents choix possibles) |
||
| Ligne 34 : | Ligne 34 : | ||
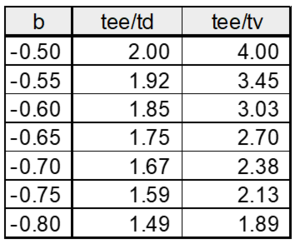
| − | [[File:durée_en_eau.png| | + | [[File:durée_en_eau.png|300px|center|thumb|<center>''<u>Figure 1</u> : Rapport entre les durées maximales en eau réelles pour une période de retour donnée et les durées de vidange (<math>tee/tv</math>) ou les durées en eau pour l’ouvrage dimensionnant (<math>tee/td</math>) avec les hypothèses de la méthode des pluies ; <u>Source</u> : Chocat'' et al.'', 2022.''</center>]] |
Ce tableau montre que la durée de vidange peut sous-estimer d'un facteur 4 la durée en eau réelle pour une même période de retour. Cette valeur est de plus elle-même sous évaluée car elle ne prend pas en compte la possibilité de pluies successives qui ne permettent pas une vidange complète entre les différents événements (risque d'autant plus fort que le débit de vidange est faible). | Ce tableau montre que la durée de vidange peut sous-estimer d'un facteur 4 la durée en eau réelle pour une même période de retour. Cette valeur est de plus elle-même sous évaluée car elle ne prend pas en compte la possibilité de pluies successives qui ne permettent pas une vidange complète entre les différents événements (risque d'autant plus fort que le débit de vidange est faible). | ||
| Ligne 41 : | Ligne 41 : | ||
| − | <center><math>tee=\left( \frac{qs}{a} \right)^{\ | + | <center><math>tee=\left( \frac{qs}{a} \right)^{\dfrac{1}{b}} </math></center> |
avec : | avec : | ||
Version du 27 juin 2023 à 15:47
Traduction anglaise : Duration with water
Dernière mise à jour : 27/06/2023
Durée pendant laquelle un ouvrage de stockage (bassin de retenue par exemple) reste en eau ; on précise généralement durée maximum en eau.
Intérêt de la notion de durée maximum en eau
Beaucoup de réglementations prescrivent une durée maximum pendant laquelle les solutions alternatives de gestion des eaux pluviales peuvent rester en eau (hormis bien sur pour les solutions avec un plan d'eau permanent - voir Bassin de retenue en eau (HU)).
Cette durée constitue en effet un paramètre important pour différentes raisons :
- Si une nouvelle pluie se produit avant que l'ouvrage ne soit entièrement vide, la capacité de stockage sera plus faible que celle prévue et peut se révéler insuffisante ; c'est en particulier pour cette raison que la méthode des pluies (qui suppose l'ouvrage toujours vide en début d'événement) conduit à des volumes systématiquement plus faibles que la méthode des volumes ;
- beaucoup d'espaces utilisés pour le stockage des eaux pluviales sont multi-fonctionnels ; les autres usages sont bien évidemment impossibles lorsque l'espace est en eau ce qui nuit à leur image et à leur intérêt ;
- avec le changement climatique le risque de maladies provoquées par les piqures de moustiques est redevenu réel ; il est donc nécessaire de limiter cette durée en eau (y compris sous forme de traces résiduelles comme des flaques) à quelques jours de façon à ne pas laisser le temps aux larves de se transformer en insectes adultes.
Nota : Comme les autres paramètres de conception, cette durée maximum en eau doit être associée à un risque de dépassement, généralement pris en compte par une période de retour.
Différents choix possibles
Différents choix sont possibles pour évaluer la durée maximum en eau d'un ouvrage.
Une solution souvent adoptée consiste à la supposer égale au temps de vidange de l'ouvrage plein. En pratique, cette solution sous-estime fortement la durée maximum en eau possible pour la même période de retour pour deux raisons de nature différente :
- elle néglige le temps nécessaire pour remplir l'ouvrage ;
- elle suppose que c'est la pluie dimensionnante (celle qui va le plus remplir l'ouvrage pour la période de retour choisie) qui sera responsable de la plus grande durée en eau.
Si la première difficulté peut facilement être levée en rajoutant au temps de vidange la durée de la pluie dimensionnante, il n'en va pas de même de la seconde. En effet des pluies moins intenses, mais beaucoup plus longues que la pluie dimensionnante peuvent maintenir l'ouvrage en eau pendant des durées beaucoup plus grandes. Il suffit en effet pour maintenir l'ouvrage en eau que le débit moyen d'apport soit supérieur au débit moyen de vidange. Chocat et al (2022) ont comparé de façon analytique trois choix possibles en utilisant la méthode des pluies :
- $ tee $ : durée maximum réelle (au sens de la méthode des pluies) pendant laquelle l'ouvrage peut être en eau pour une période de retour égale à la période de retour de dimensionnement de l'ouvrage ;
- $ tv $ : durée de vidange de l'ouvrage plein (avec un débit de vidange supposé constant) ;
- $ td $ : durée totale en eau dans le cas de l’événement dimensionnant (au sens de la méthode des pluies $ td $ est égal à la somme de la durée de la pluie dimensionnante et du temps de vidange).
Ils ont montré que les rapports entre ces grandeurs ne dépendaient (avec les hypothèses de la méthode des pluies) que de la valeur du coefficient $ b $ de la formule de Montana permettant d'ajuster la courbe IDF correspondant à la région pluviométrique et à la période de retour choisie
Le tableau de la figure 1 synthétise les résultats obtenus pour les valeurs usuelles de $ b $.
Ce tableau montre que la durée de vidange peut sous-estimer d'un facteur 4 la durée en eau réelle pour une même période de retour. Cette valeur est de plus elle-même sous évaluée car elle ne prend pas en compte la possibilité de pluies successives qui ne permettent pas une vidange complète entre les différents événements (risque d'autant plus fort que le débit de vidange est faible).
En conséquence, il paraît largement préférable d'utiliser la valeur de la durée en eau calculée avec la formule de la méthode des pluies (éventuellement pour une période de retour différente de celle utilisée pour calculer le volume) :
avec :
- $ tee $ : durée en eau (en h) ;
- $ qs $ : débit moyen spécifique (en mm/h);
- $ a $ et $ b $ : coefficients de la formule de Montana fonction de la région pluviométrique et de la période de retour (avec les unités ad hoc).
Bibliographie :
- Chocat, B., Afrit, B., Maytraud, T., Savary, P., Tedoldi, D. (2022) : Comment mettre en place des règles hydrologiques efficaces pour la gestion durable des eaux pluviales urbaines ; TSM n°10 ; octobre 2022 ; pp.39-62.
 S'abonner à un flux RSS
S'abonner à un flux RSS