Muskingum (Modèle) (HU) : Différence entre versions

Version actuelle en date du 23 mai 2024 à 17:17

Traduction anglaise : Muskingum's model

Dernière mise à jour : 23/05/2024

Modèle de propagation d’ondes permettant l’étude de la propagation des crues dans les systèmes hydrauliques.

Sommaire

1 Utilisation du modèle
2 Éléments d'historique
3 Concept de base et formulation
4 Mise en œuvre pratique
5 Estimation des paramètres
6 Extension au modèle Muskingum-Cunge
7 Conclusions sur la méthode
8 Bibliographie

[modifier] Utilisation du modèle

Ce modèle peut également être utilisé dans les modèles hydrologiques comme fonction de transfert. Il permet de calculer l'hydrogramme sortant d'un tronçon de rivière ou de réseau si l'on connaît l'hydrogramme qui y rentre

Dans tous les cas le modèle Muskingum représente le décalage temporel et l'amortissement.

[modifier] Éléments d'historique

D’après Linsley & al. (1949), le modèle serait dû à G.T. Mac Carthy de l’US army corps of engineers (USACE). Il aurait été développé vers 1934, présenté à une conférence de la division de l’Atlantique nord de l’USACE, et publié pour la première fois en 1940 dans un manuel sur le contrôle des crues (Mc Carthy, 1940). Selon (Diskin, 1967), il aurait ensuite reçu l’agrément de B.R. Gilcrest (1950) et de V.T. Chow (1959).

Durant une quarantaine d’années, le modèle Muskingum fera l’objet de multiples articles de la part d’hydrologues aussi conséquents que Overton, Nash, Dooge, etc. L’une des approche les plus intéressantes reste celle de J.A. Cunge (1969). Ce travail démontre en effet clairement les raisons pour lesquelles une solution numérique explicite de l’équation différentielle du modèle de Muskingum peut approcher numériquement la solution du modèle de l’onde de crue diffusante.

Nota : le nom du modèle fait référence à la rivière Muskingum dans l’Etat de l’Ohio, longue de 179 km et sous-affluent du Mississipi sur laquelle le modèle a été utilisé pour la première fois.

[modifier] Concept de base et formulation

Le modèle Muskingum repose sur l'hypothèse, d’ailleurs vérifiée ultérieurement par Hicks (1943), que le volume stocké dans une portion de bief de rivière est sensiblement proportionnel au débit qui s'y écoule.

Il est donc possible de combiner l'équation de continuité :

$ \frac{dV_s(t)}{dt}=Q_e(t)-Q_s(t) \quad(1) $

avec une équation de stockage à deux paramètres, $ K $ et $ x $, qui relie le volume stocké à une combinaison linéaire des débits entrant et sortant :

$ V_s(t)=K.\left[x.Q_e(t)-(1-x).Q_s(t) \right] \quad(2) $

avec :

$ V_s(t) $ : volume stocké dans le bief à l’instant $ t $ (m³) ;
$ Q_e(t) $ : débit entrant dans le bief (m³/s) ;
$ Q_s(t) $ : débit sortant du bief (m³/s) ;
$ K $ : paramètre assimilable à un temps moyen de transfert (s) ;
$ x $ : paramètre sans dimension compris entre 0 et 1.

En combinant les équations (1) et (2), et en intégrant l'équation différentielle résultante avec $ K $ et $ x $ constants, on obtient une expression permettant le calcul direct de $ Q_s(t) $ :

$ Q_s(t)= \frac{1}{K.(1-x)^2}. \int_0^t Q_e(τ).e^{-(t-τ)/K(1-x)}.dτ + \frac{x}{1-x}Q_e(0) \quad(3) $

[modifier] Mise en œuvre pratique

Sur le plan pratique l'équation (3) peut être formulée en mettant en œuvre une discrétisation des fonctions $ Q_e(t) $ et $ Q_s(t) $ sous la forme de tables de valeurs numériques. On construit alors une formule de récurrence de la forme :

$ Q_s(t+Δt)= C_1.Q_e(t)+C_2.Q_e(t+Δt)+C_3.Q_s(t) \quad(4) $

La construction de ce modèle peut se faire de plusieurs façons. La démarche la plus classique consiste à combiner les équations (1) et (2), puis à résoudre l'équation différentielle obtenue par la méthode des différences finies. Selon le schéma de discrétisation retenu, plusieurs formulations peuvent être obtenues. La plus classique est la suivante :

$ C_1= \frac{2.K.x+Δt}{2.K.(1-x)+Δt}\qquad C_2= \frac{Δt - 2.K.x}{2.K.(1-x)+Δt}\qquad C_3= \frac{2.K.(1-x)+Δt}{2.K.(1-x)+Δt} \quad(5) $

[modifier] Estimation des paramètres

Si l'on fait l'hypothèse que le premier paramètre $ x $ est sans dimension, alors le paramètre $ K $ devient analogue à un temps et représente le décalage temporel entre les centres de gravité de l'entrée et de la sortie (lag time). Le paramètre $ K $ est donc théoriquement égal à la longueur du tronçon divisée par la célérité moyenne de l'onde. Il est donc possible de le calculer en utilisant la célérité de Kleitz-Seddon.

Différentes études empiriques (Reynier, 1978), (Kovacs, 1988), (Semsar, 1995), ont cependant montré que d'autres relations entre la célérité moyenne de l'onde et la vitesse de l'eau en régime uniforme, correspondant à une valeur du débit proche du débit maximum ($ Q_{max} $) permettait une meilleure représentation. Ainsi par exemple Semsar (1995) a montré que la relation suivante donnait de bons résultats :

$ K = \frac{Δx}{0{,}8.V(0{,}8.Q_{max})}\quad(13) $

Avec :

$ V(0{,}8.Q_{max}) $ : vitesse qui correspond à un débit égal à 80% du débit maximum $ Q_{max} $

La réponse du modèle est peu sensible au choix de la valeur de $ x $ (Reynier, 1978). Il est souvent recommandé de retenir la valeur $ x = 0{,}2 $. La valeur $ x = 0 $ correspond au modèle du réservoir linéaire.

[modifier] Extension au modèle Muskingum-Cunge

Le schéma explicite représenté par les équations (4) et (5) est en réalité une solution numérique médiocre de l’équation intégrale (3). Il introduit en effet une diffusion numérique artificielle dont l'effet sur la déformation de l'hydrogramme conditionne très fortement le résultat obtenu. Cunge (1969) a montré qu’en "pilotant" cette diffusion numérique, à l’aide des paramètres $ K $, $ x $ et $ Δt $, ce modèle, en théorie peu adéquat pour représenter une propagation d’onde (l’équation différentielle (1) est du premier ordre), pouvait donner une solution numérique satisfaisante d’une équation différentielle du second ordre, caractéristique d’une onde de crue diffusante. Le "pilotage" des paramètres proposé par Cunge répond aux équations suivantes :

$ K = \frac{Δx}{c}\quad(7) $

$ x = \frac{1}{2.\left[1-\frac{K.Q}{Δx^2.B.I} \right]}\quad(8) $

$ c = \frac{dQ}{dS}\quad(9) $

Avec (voir figure 1) :

$ Δx $ : longueur du tronçon (m) ;
$ c $ : célérité de l'onde (m/s) ;
$ B $ : largeur de la surface libre (m) ;
$ S $ : Section mouillée (m²) ;
$ I $ : pente (m/m) ;
$ Q $ : débit en régime permanent correspondant aux valeurs de $ B $, $ I $ et $ S $ (m³/s).

Figure 1 : Signification des paramètres dans la formule de Cunge.

[modifier] Conclusions sur la méthode

Cet exemple montre bien la prudence dont on doit faire preuve dans l’interprétation "physique" des résultats numériques des modèles conceptuels. Ainsi, le schéma en différences finies (4) et (5) peut ne plus avoir numériquement de rapport avec le modèle initial, dont le comportement exact est traduit par l’équation (4). Les manipulations numériques, dont ce dernier a été l’objet, ont ainsi abouti à une analogie numérique avec un autre modèle celui de l’onde diffusante. Certes, les équations (7) à (9) correspondent, de la part de Cunge, à des "manipulations raisonnées". Elles ont pour objectif d’autoriser le calcul d’un modèle diffusant à l’aide d’un schéma explicite qui permet des calculs très rapides sans nécessiter de recueil de données important. Cependant de nombreuses manipulations numériques "moins" raisonnées ont fréquemment conduit à de prétendues interprétations physiques des comportements des modèles conceptuels en hydrologie (Desbordes, 1987).

Malgré tout le modèle Muskingum, même sous sa forme la plus simple, donne souvent de bons résultats dans la mesure où l'on ne s'intéresse qu'à la déformation des hydrogrammes à l'intérieur du système d'assainissement (Semsar, 1995) ou du réseau hydrographique naturel. Il est bien évidemment totalement inadapté pour représenter l'effet de singularités hydrauliques locales provoquant des remontées de ligne d'eau ou des phénomènes complexes comme les mises en charge ou des débordements.

[modifier] Bibliographie

Chow, V.T. (1959) : Open channel hydraulics ; Mac Graw-Hill books company - New-York.
Cunge, J.A. (1969) : Au sujet d'une méthode de propagation de crue ; Journal of Hydraulics Research ; n°7 ; 1969 ; pp 205-230.
Desbordes, M. (1987) : Contribution à l'analyse et à la modélisation des mécanismes hydrologiques en milieu urbain ; thèse d'état ; université de Montpellier ; France ; 242 p.
Diskin, M.M. (1962) : A basic study of the linearity of rainfall runoff process in watersheds ; Ph D. Thesis ; Univ of Ilinois.
Gilcrest, B.R. (1950) : Flood routing, ch. 10 of Engineering hydraulics ; John Willey and sons - New-York.
Hicks, W.I. (1943) : A method of computing urban runoff ; Transactions of the ASCE ; paper n°2230 ; pp 1217-1253.
Kovacs, Y. (1988) : Modèles de simulation des écoulements transitoires en réseaux d’assainissement ; thèse de Docteur ingénieur ; ENPC Paris - France ; 183 p.
Linsley, R.K., Kohler, M.A., Paulhus, J.L.H. (1949) : Applied hydrology ; Mac Graw-Hill books company - New-York.
Mac Carthy, G.T. (1940) : Engineering construction : flood control ; The engineering school ; Fort Belvoir, Virginia, USA.
Reynier, B. (1978) : Étude d'un modèle hydrologique urbain ; rapport de DEA ; INSA de Lyon - France ; 1978.
Semsar, Y.A. (1995) : Mise au point d'une méthodologie d'évaluation et de comparaison des modèles de simulation hydrauliques des réseaux d'assainissement ; Doctorat, INSA de Lyon, n°95ISAL0025 ; 272 p.

@@ Ligne 1 : / Ligne 1 : @@
 ''<u>Traduction anglaise</u> : Muskingum's model''
-[[Modèle de propagation d’ondes de crue (HU)|Modèle de propagation d’ondes]] permettant l’étude de la propagation des crues dans les systèmes hydrauliques.
+<u>Dernière mise à jour</u> : 23/05/2024
+[[Modèle de propagation d’ondes de crue (HU)|Modèle de propagation d’ondes]] permettant l’étude de la propagation des crues dans les systèmes hydrauliques.
+==Utilisation du modèle==
 Ce modèle peut également être utilisé dans les [[Modèle hydrologique (HU)|modèles hydrologiques]] comme [[Fonction de production et fonction de transfert (HU)|fonction de transfert]]. Il permet de calculer [[Hydrogramme (HU)|l'hydrogramme]] sortant d'un tronçon de rivière ou de réseau si l'on connaît l'hydrogramme qui y rentre
-Dans tous les cas le modèle Muskingum représente le décalage temporel et l'amortissement.
+Dans tous les cas le modèle Muskingum représente le décalage temporel et l'[[Amortissement d'un hydrogramme (HU)|amortissement]].
 ==Éléments d'historique==
-D’après Linsley & al. (1949), le modèle serait dû à G.T. Mac Carthy de l’US army corps of engineers (USACE). Il aurait été développé vers 1934, présenté à une conférence de la division de l’Atlantique nord de l’USACE, et publié pour la première fois en 1940 dans un manuel sur le contrôle des crues (Mc Carthy, 1940).
+D’après Linsley & al. (1949), le modèle serait dû à G.T. Mac Carthy de l’''US army corps of engineers (USACE)''. Il aurait été développé vers 1934, présenté à une conférence de la division de l’Atlantique nord de l’USACE, et publié pour la première fois en 1940 dans un manuel sur le contrôle des crues (Mc Carthy, 1940). Selon (Diskin, 1967), il aurait ensuite reçu l’agrément de B.R. Gilcrest (1950) et de V.T. Chow (1959).
-Selon (Diskin, 1967), il aurait ensuite reçu l’agrément de B.R. Gilcrest (1950) et de V.T. Chow (1959).
-Durant une quarantaine d’années, le modèle Muskingum fera l’objet de multiples articles de la part d’hydrologues aussi conséquents que Overton, Nash, Dooge, etc.. L’une des approche les plus intéressantes reste celle de J.A. Cunge (1969). Ce travail démontre en effet clairement les raisons pour lesquelles une solution numérique explicite de l’équation différentielle du modèle de Muskingum peut approcher numériquement la solution du modèle de l’onde de crue diffusante.
+Durant une quarantaine d’années, le modèle Muskingum fera l’objet de multiples articles de la part d’hydrologues aussi conséquents que Overton, Nash, Dooge, etc. L’une des approche les plus intéressantes reste celle de J.A. Cunge (1969). Ce travail démontre en effet clairement les raisons pour lesquelles une solution numérique explicite de l’équation différentielle du modèle de Muskingum peut approcher numériquement la solution du modèle de l’[[Onde de crue diffusante (modèle de l') (HU)|onde de crue]] diffusante.
-<u>Nota</u> : le nom du modèle fait référence à la rivière Muskingum dans l’Etat de l’Ohio, longue de 179 km et sous-affluent su Mississipi sur laquelle le modèle a été utilisé pour la première fois.
+<u>Nota</u> : le nom du modèle fait référence à la rivière Muskingum dans l’Etat de l’Ohio, longue de 179 km et sous-affluent du Mississipi sur laquelle le modèle a été utilisé pour la première fois.
 ==Concept de base et formulation==
@@ Ligne 20 : / Ligne 23 : @@
 Le modèle Muskingum repose sur l'hypothèse, d’ailleurs vérifiée ultérieurement par Hicks (1943), que le volume stocké dans une portion de bief de rivière est sensiblement proportionnel au débit qui s'y écoule.
-Il est donc possible de combiner l'équation de continuité :
+Il est donc possible de combiner l'[[Continuité (équation de) (HU)|équation de continuité]] :
 <center><math>\frac{dV_s(t)}{dt}=Q_e(t)-Q_s(t) \quad(1)</math></center>
 avec une équation de stockage à deux paramètres, <math>K</math> et <math>x</math>, qui relie le volume stocké à une combinaison linéaire des débits entrant et sortant :
@@ Ligne 29 : / Ligne 33 : @@
 <center><math>V_s(t)=K.\left[x.Q_e(t)-(1-x).Q_s(t)    \right] \quad(2)</math></center>
 avec :
-* <math>V_s(t)</math> :	volume stocké dans le bief à l’instant <math>t</math> (<math>m^3</math>) ;
+* <math>V_s(t)</math> :	volume stocké dans le bief à l’instant <math>t</math> (m<sup>3</sup>) ;
-* <math>Q_e(t)</math> :	débit entrant dans le bief (<math>m^3/s</math>) ;
+* <math>Q_e(t)</math> :	débit entrant dans le bief (m<sup>3</sup>/s) ;
-* <math>Q_s(t)</math> :	débit sortant du bief (<math>m^3/s</math>) ;
+* <math>Q_s(t)</math> :	débit sortant du bief (m<sup>3</sup>/s) ;
-* <math>K</math> : paramètre assimilable à un temps moyen de transfert (<math>s</math>) ;
+* <math>K</math> : paramètre assimilable à un temps moyen de transfert (s) ;
 * <math>x</math> : paramètre sans dimension compris entre 0 et 1.
-En combinant les équations (1) et (2), et en intégrant l'équation différentielle résultante avec <math>K</math> et <math>x</math> constants on obtient une expression permettant le calcul direct de <math>Q_s(t)</math> :
+En combinant les équations (1) et (2), et en intégrant l'équation différentielle résultante avec <math>K</math> et <math>x</math> constants, on obtient une expression permettant le calcul direct de <math>Q_s(t)</math> :
@@ Ligne 44 : / Ligne 49 : @@
 ==Mise en œuvre pratique==
-Sur le plan pratique l'équation (3) peut être formulée en mettant en œuvre une discrétisation des fonctions Q_e(t) et Q_s(t) sous la forme de tables de valeurs numériques. On construit alors une formule de récurrence de la forme :
+Sur le plan pratique l'équation (3) peut être formulée en mettant en œuvre une discrétisation des fonctions <math>Q_e(t)</math> et <math>Q_s(t)</math> sous la forme de tables de valeurs numériques. On construit alors une formule de récurrence de la forme :
 <center><math>Q_s(t+Δt)= C_1.Q_e(t)+C_2.Q_e(t+Δt)+C_3.Q_s(t) \quad(4)</math></center>
 La construction de ce modèle peut se faire de plusieurs façons. La démarche la plus classique consiste à combiner les équations (1) et (2), puis à résoudre l'équation différentielle obtenue par la méthode des différences finies. Selon le schéma de discrétisation retenu, plusieurs formulations peuvent être obtenues. La plus classique est la suivante :
-<center><math>C_1= \frac{2.K.x+Δt}{2.K.(1-x)+Δt}\qquad C_2= \frac{Δt - 2.K.x}{2.K.(1-x)+Δt}\qquad C_3= \frac{2.K.(1-x)+Δt}{2.K.(1-x)+Δt}</math></center>
+<center><math>C_1= \frac{2.K.x+Δt}{2.K.(1-x)+Δt}\qquad C_2= \frac{Δt - 2.K.x}{2.K.(1-x)+Δt}\qquad C_3= \frac{2.K.(1-x)+Δt}{2.K.(1-x)+Δt} \quad(5)</math></center>
 ==Estimation des paramètres==
-Si l'on fait l'hypothèse que le premier paramètre <math>x</math> est sans dimension, alors le paramètre <math>K</math> devient analogue à un temps et représente le décalage temporel entre les centres de gravité de l'entrée et de la sortie (lag time). Le paramètre <math>K</math> est donc théoriquement égal à la longueur du bief divisée par la célérité moyenne de l'onde. La plupart des auteurs (Reynier, 1978), (Kovacs, 1988), (Semsar, 1995), proposent d'approcher la célérité moyenne de l'onde par une fonction de la vitesse de l'eau en régime uniforme, correspondant à une valeur du débit proche du débit maximum (<math>Q_{max}</math>). Ainsi par exemple Semsar (1995) a montré que la relation suivante donnait de très bons résultats :
+Si l'on fait l'hypothèse que le premier paramètre <math>x</math> est sans dimension, alors le paramètre <math>K</math> devient analogue à un temps et représente le décalage temporel entre les centres de gravité de l'entrée et de la sortie ([[Lag time (HU)|lag tim]]e). Le paramètre <math>K</math> est donc théoriquement égal à la longueur du tronçon divisée par la [[Célérité (HU)|célérité]] moyenne de l'onde. Il est donc possible de le calculer en utilisant la [[Kleitz-Seddon (célérité de) (HU)|célérité de Kleitz-Seddon]].
+Différentes études empiriques (Reynier, 1978), (Kovacs, 1988), (Semsar, 1995), ont cependant montré que d'autres relations entre la célérité moyenne de l'onde et la vitesse de l'eau en régime uniforme, correspondant à une valeur du débit proche du débit maximum (<math>Q_{max}</math>) permettait une meilleure représentation. Ainsi par exemple Semsar (1995) a montré que la relation suivante donnait de bons résultats :
+<center><math>K = \frac{Δx}{0{,}8.V(0{,}8.Q_{max})}\quad(13)</math></center>
+Avec :
+* <math>V(0{,}8.Q_{max})</math> : vitesse qui correspond à un débit égal à 80% du débit maximum <math>Q_{max}</math>
-La réponse du modèle est peu sensible au choix de la valeur de <math>x</math> (Reynier, 1978). Il est souvent recommandé de retenir la valeur <math>x = 0{,}2</math>. La valeur <math>x = 0</math> correspond au modèle du réservoir linéaire.
+La réponse du modèle est peu sensible au choix de la valeur de <math>x</math> (Reynier, 1978). Il est souvent recommandé de retenir la valeur <math>x = 0{,}2</math>. La valeur <math>x = 0</math> correspond au [[Réservoir linéaire (modèle du) (HU)|modèle du réservoir linéaire]].
-''mot en chantier''
+==Extension au modèle Muskingum-Cunge==
+Le schéma explicite représenté par les équations (4) et (5) est en réalité une solution numérique médiocre de l’équation intégrale (3). Il introduit en effet une diffusion numérique artificielle dont l'effet sur la déformation de l'hydrogramme conditionne très fortement le résultat obtenu. Cunge (1969) a montré qu’en "pilotant" cette diffusion numérique, à l’aide des paramètres <math>K</math>, <math>x</math> et <math>Δt</math>, ce modèle, en théorie peu adéquat pour représenter une propagation d’onde (l’équation différentielle (1) est du premier ordre), pouvait donner une solution numérique satisfaisante d’une équation différentielle du second ordre, caractéristique d’une [[Onde de crue diffusante (modèle de l') (HU)|onde de crue diffusante]]. Le "pilotage" des paramètres proposé par Cunge répond aux équations suivantes :
+<center><math>K = \frac{Δx}{c}\quad(7)</math></center>
+<center><math>x = \frac{1}{2.\left[1-\frac{K.Q}{Δx^2.B.I} \right]}\quad(8)</math></center>
+<center><math>c = \frac{dQ}{dS}\quad(9)</math></center>
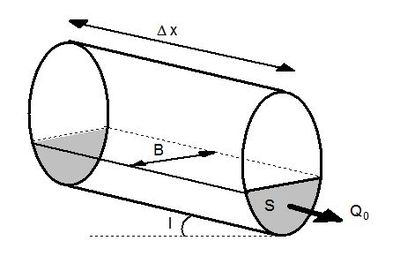
+Avec (voir ''figure 1'') :
+* <math>Δx</math> : longueur du tronçon (m) ;
+* <math>c</math> : célérité de l'onde (m/s) ;
+* <math>B</math> : largeur de la surface libre (m) ;
+* <math>S</math> : Section mouillée (m<sup>2</sup>) ;
+* <math>I</math> : pente (m/m) ;
+* <math>Q</math> : débit en régime permanent correspondant aux valeurs de <math>B</math>, <math>I</math> et <math>S</math> (m<sup>3</sup>/s).
+[[File:muskingum.JPG|400px|center|thumb|<center>''<u>Figure 1</u> : Signification des paramètres dans la formule de Cunge.''</center>]]
+==Conclusions sur la méthode==
+Cet exemple montre bien la prudence dont on doit faire preuve dans l’interprétation "physique" des résultats numériques des modèles conceptuels. Ainsi, le schéma en différences finies (4) et (5) peut ne plus avoir numériquement de rapport avec le modèle initial, dont le comportement exact est traduit par l’équation (4). Les manipulations numériques, dont ce dernier a été l’objet, ont ainsi abouti à une analogie numérique avec un autre modèle celui de l’onde diffusante. Certes, les équations (7) à (9) correspondent, de la part de Cunge, à des "manipulations raisonnées". Elles ont pour objectif d’autoriser le calcul d’un modèle diffusant à l’aide d’un schéma explicite qui permet des calculs très rapides sans nécessiter de recueil de données important. Cependant de nombreuses manipulations numériques "moins" raisonnées ont fréquemment conduit à de prétendues interprétations physiques des comportements des modèles conceptuels en hydrologie (Desbordes, 1987).
+Malgré tout le modèle Muskingum, même sous sa forme la plus simple, donne souvent de bons résultats dans la mesure où l'on ne s'intéresse qu'à la déformation des hydrogrammes à l'intérieur du système d'assainissement (Semsar, 1995) ou du réseau hydrographique naturel. Il est bien évidemment totalement inadapté pour représenter l'effet de singularités hydrauliques locales provoquant des remontées de ligne d'eau ou des phénomènes complexes comme les [[Mise en charge (HU)|mises en charge]] ou des [[Débordement (HU)|débordements]].
 ==Bibliographie==
 * Chow, V.T. (1959) : Open channel hydraulics ; Mac Graw-Hill books company - New-York.
 * Cunge, J.A. (1969) : Au sujet d'une méthode de propagation de crue ; Journal of Hydraulics Research ; n°7 ; 1969 ; pp 205-230.
+* Desbordes, M. (1987) : Contribution à l'analyse et à la modélisation des mécanismes hydrologiques en milieu urbain ; thèse d'état ; université de Montpellier ; France ; 242 p.
 * Diskin, M.M. (1962) : A basic study of the linearity of rainfall runoff process in watersheds ; Ph D. Thesis ; Univ of Ilinois.
 * Gilcrest, B.R. (1950) : Flood routing, ch. 10 of Engineering hydraulics ; John Willey and sons - New-York.
@@ Ligne 76 : / Ligne 120 : @@
 * Semsar, Y.A. (1995) : Mise au point d'une méthodologie d'évaluation et de comparaison des modèles de simulation hydrauliques des réseaux d'assainissement ; Doctorat, INSA de Lyon, n°95ISAL0025 ; 272 p.
+[[Catégorie:Dictionnaire_DEHUA]]
 [[Catégorie:Modélisation_des_écoulements_en_réseau_et_en_rivière_(HU)]]