Modèle d'écoulement en réseau et en cours d'eau (HU)

Traduction anglaise : Design méthods for pipes and channels

Dernière mise à jour : 01/05/2024

Mot en chantier

Modèle, généralement écrit sous une forme mathématique, permettant de représenter la propagation d'une onde de crue dans un système hydraulique (réseau d'assainissement ou réseau hydrographique de surface) et/ou de calculer les hauteurs d'eau atteintes et de déterminer les zones potentiellement inondées.

Fonctions des modèles d'écoulement

Les modèles d'écoulement font généralement suite à des modèles hydrologiques dans une représentation parfois dite semi-distribuée du système hydrologique simulé (figure 1). Les modèles hydrologiques produisent des hydrogrammes aux exutoires des bassins versants et ces hydrogrammes sont ensuite propagés dans les tronçons du réseau hydrographique et combinés aux jonctions par les modèles d'écoulement. Ils nécessitent également une représentation adaptée de ce réseau hydrographique.

Figure 1 à mettre

Les modèles d'écoulement doivent donc remplir différentes fonctions :

• représenter le décalage temporel et l'amortissement de l'hydrogramme de crue lors de son transfert dans un tronçon ;
• représenter la composition des hydrogrammes aux jonctions, et leur séparation éventuelle aux défluences ;
• représenter l'impact des différents ouvrages (en particulier de stockage : seuil, barrage, bassin de retenue, etc.) et singularités hydrauliques (seuils, chutes, influences aval, etc.) sur la façon dont l'hydrogramme est transféré.

Ces fonctions obligatoires sont complétées par des fonctions supplémentaires qui peuvent être remplies par le modèle lui-même ou par un post-traitement (voir le § suivant) :

• représenter les grandeurs hydrauliques (hauteur et vitesse) associées aux valeurs de débit ;
• en déduire les hauteurs d'eau atteintes dans le lit majeur et l'extension éventuelle de la zone inondée.

Modèles hydrauliques et modèles de transfert d'onde

Il existe trois grandes familles de modèles :

• les modèles issus de la Mécanique des fluides qui résolvent numériquement les équations de Navier-Stokes à 2, 3 ou 4 dimensions ;
• les modèles utilisant les équations de Barré de Saint Venant à 1 ou 2 dimensions ;
• les modèles conceptuels de transfert d'onde.

Modèles issus de la MFN

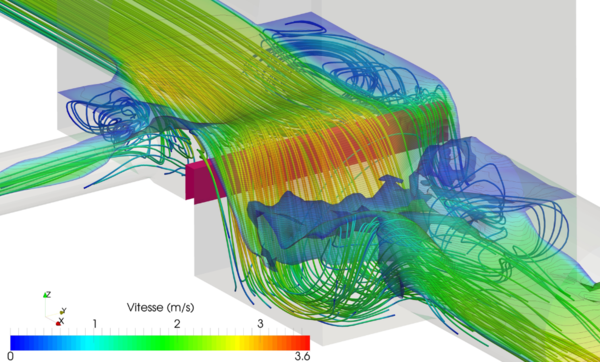
Les modèles de mécanique des fluides numérique sont aujourd'hui des outils extrêmement puissants, capables de représenter les écoulements à surface libre, en régime permanent ou transitoire, avec 1, 2 ou 3 dimensions d'espace (figure 2). Ils sont cependant extrêmement gourmands en temps calcul et en place mémoire et ne sont encore utilisés que pour des applications limitées ne concernant qu'un petit linéaire et/ou une singularité hydraulique. Ils sont cités ici pour mémoire car il est possible que dans quelques années les progrès de l'informatique permettent de les utiliser de façon opérationnelle pour représenter des systèmes hydrauliques complets.

Figure 2 : Évolution de la surface libre dans un déversoir frontal calculée avec un outil de Mécanique des fluides numérique ; Crédit José Vazquez.

Pour en savoir plus, voir l'article Mécanique des fluides numérique / MFN (HU).

Modèles utilisant les équations de Barré de Saint Venant

Les équations de Barré de Saint Venant permettent de représenter les écoulements à surface libre non permanents, unidimensionnels ou bidimensionnels, moyennant deux hypothèses fortes : l'écoulement doit être graduellement varié et la répartition des pressions doit être hydrostatique.

Même si ces hypothèses ne sont pas toujours vérifiées, en particulier dans le cas des crues rapides, l'expérience montre que ce modèle permet de représenter la propagation des crues de façon très satisfaisante, que ce soit en rivière ou en réseau d'assainissement. De plus, comme il utilise la vitesse et la section mouillée (ou la hauteur d'eau) comme variables principales de calcul il est également capable de calculer les lignes d'eau, et, dans le cas des équations bidimensionnelles, de déterminer les zones inondées.

Les équations de Barré de Saint Venant s'écrivent sous la forme synthétique suivante :

à une dimension

$ \frac{\partial U}{\partial t}+\frac{\partial F(U)}{\partial x}=S(U) \quad(1) $

et, à deux dimensions :

$ \frac{\partial U}{\partial t}+\frac{\partial F(U)}{\partial x}+\frac{\partial F(U)}{\partial y}=S(U) \quad(2) $

Dans les deux cas :

• $ U = \displaystyle\binom{S}{V} \quad(3) $ représente le vecteur des variables conservatives ;
• $ F(U) = \displaystyle\binom{Q}{\frac{V^2}{2} + g.h}\quad(4) $ représente les flux ;
• $ S(U) = \displaystyle\binom{q}{g.(I-J)} \quad(5) $ représente les termes sources ;

Avec :

• $ h $ : Hauteur d'eau (m) ;
• $ S $ : Section mouillée (m²) ;
• $ V $ : Vitesse moyenne dans la section droite (m/s) ( $ Q = V.S $);
• $ Q $ : Débit (m³/s) ;
• $ g $ : Accélération de la pesanteur (m/s²) ;
• $ q $ : Apport ou perte latérale de débit (m³/s)
• $ I $ : Pente du fond (m/m) ;
• $ J $ : Pertes de charge par unité de longueur (pente de la ligne d'énergie) (m/m).

Les différents termes apparaissant dans la deuxième équation de Barré de Saint Venant peuvent prendre des valeurs très variées et il arrive souvent que certains soient négligeable par rapport aux autres. Il est alors possible de simplifier cette équation et de construire des modèles plus faciles à intégrer. La simplification la plus courante consiste à considérer les termes d'inertie et d'accélération convective comme négligeables. On obtient alors le modèle de l'onde de crue diffusante :

$ g.\frac{\partial h}{\partial x}=g.(I-J)\qquad(6) $

Même s'ils donnent des résultats souvent acceptables dans de nombreux cas, ces modèles simplifiés ont perdu beaucoup d'intérêt avec le développement d'ordinateurs et de logiciels qui permettent de résoudre rapidement les équations complètes, même sur des réseaux complexes.

Pour en savoir plus, voir l'article Barré de Saint Venant (équations de) (HU).

Modèles conceptuels de transfert d'onde

Les modèles de propagation d'onde de crue sont des modèles conceptuels permettant de simuler la propagation des ondes de crue dans un système hydrologique.

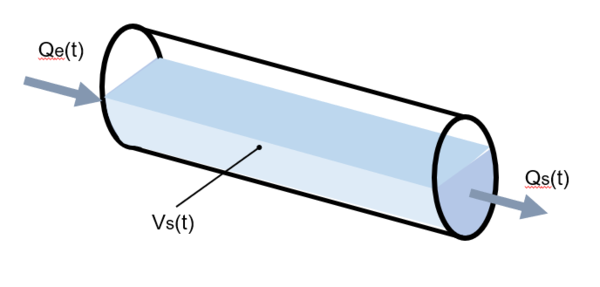
Ces modèles reposent sur l'équation de continuité (relation 6) auxquels on associe généralement une équation de stockage reliant le volume stocké dans le tronçon aux débits observés ou simulés aux extrémités amont (débit entrant) et/ou aval (débit sortant) du tronçon (relation 7 et figure 3) :

$ Q_s(t) = Q_e(t)- \frac{dV_s(t)}{dt}\qquad(7) $

$ V_s(t) = f(t, Q_e(t), Q_s(t))\qquad(8) $

Avec :

• $ Q_e(t) $ : débit à l'entrée du tronçon (m³/s) ;
• $ Q_s(t) $ : débit à la sortie du tronçon (m³/s) ;
• $ V_s(t) $ : volume stocké dans le tronçon (m³).

Figure 3 : Dans les modèles de propagation d'onde de crue, la deuxième équation est le plus souvent obtenue en reliant le volume stocké dans le tronçon aux débits amont et aval par une expression simple, souvent linéaire.

Les modèles de transfert d'onde les plus connus sont le modèle Muskingum, le modèle de translation simple et le modèle de stock. Dans certains cas, il est même possible d'établir un lien entre ces modèles conceptuels et les modèles simplifiés issus des équations de Barré de Saint Venant.

Pour en savoir plus, voir l'article Modèle de propagation d’ondes de crue (HU)