Méthode des débits (HU) : Différence entre versions

Version actuelle en date du 31 juillet 2023 à 09:54

Traduction anglaise : Flows design method

Dernière mise à jour : 31/07/2023

Modèle permettant de simuler le fonctionnement des ouvrages de stockage (bassins de retenue ou autre technique alternative), quel que soit le mode de régulation des débits sortants.

[modifier] Principes de la méthode

La méthode des débits consiste à simuler en continu le fonctionnement de l'ouvrage avec un pas de temps court (de quelques minutes à quelques dizaines de minutes). La simulation est normalement faite sur une durée longue (typiquement plusieurs dizaines d'années) en utilisant en entrée une chronique locale de pluies.

L'application d'un modèle hydrologique (ou dans les cas compliqués d'un modèle de simulation plus détaillé) permet de transformer les intensités de pluie en une fonction représentant le débit entrant dans l'ouvrage en fonction du temps : $ Q_e(t) $

On utilise ensuite l'équation de conservation pour calculer à chaque instant la valeur du volume stocké $ V_s(t) $ et du débit de sortie $ Q_s(t) $ :

$ \frac{dV_s(t)}{dt} = Q_e(t) - Q_s(t) \quad (1) $

La résolution de cette équation est généralement faite numériquement par la méthode des différences finies en discrétisant les différentes variables.

On utilise souvent la variable intermédiaire $ H(t) $ qui représente la hauteur d'eau dans l'ouvrage. Les deux autres variables, $ V_s(t) $ et $ Q_s(t) $ sont en effet généralement reliées directement à $ H(t) $.

par une relation de stockage décrivant l'évolution du volume stocké $ V_s(t) $ en fonction de la hauteur d'eau dans le bassin, $ h (t) $ :

$ V_s(t) = f \lgroup h(t)\rgroup \quad (2) $

par une (ou des) relation(s) de vidange décrivant l'évolution du débit de sortie $ Q_s(t) $ du bassin en fonction de la hauteur d'eau dans le bassin :

$ Q_s(t) = g \lgroup h(t)\rgroup \quad (3) $

Avec :

$ Qe(t $) : débit entrant dans l'ouvrage de stockage (m³/s) ;
$ Qs(t) $ : débit sortant (m³/s) ;
$ h(t) $ : hauteur d’eau dans l’ouvrage (m) ;
$ Vs(t) $ : volume stocké dans l'ouvrage (m³).

La hauteur d'eau et le volume stocké dans le bassin ainsi que le débit sortant peuvent alors être calculés en fonction du temps, en résolvant numériquement le système constitué par les équations (1), (2) et (3) et il est possible de déduire la valeur du volume stocké maximum ($ Vmax $) pour chaque événement simulé (figure 1).

Figure 1 : Évolution des différentes grandeurs en fonction du temps pour un événement pluvieux donné.

[modifier] Analyse des résultats

Cette simulation produit en sortie des chroniques de hauteurs d'eau, de débits de sortie et de volumes stockés, associées au pas de temps de calcul choisi.

On peut donc facilement compter le nombre de valeurs qui, pour la variable d'intérêt, dépassent un seuil donné et en déduire la durée de dépassement pendant la durée de simulation. On peut par exemple calculer le nombre de pas de temps pendant lequel (c'est à dire la durée totale pendant laquelle) le volume à stocker a été supérieur à une valeur donnée.

Ce résultat est cependant difficilement exploitable en termes de fréquence de dépassement (ou de période de retour) car il mélange deux notions différentes : le nombre de fois ou le volume à dépassé la valeur choisie et la durée de chacun des dépassements. Pour éviter cet inconvénient il est donc nécessaire de compléter le raisonnement, ce qui peut se faire de deux façons différentes :

Soit on raisonne par période temporelle (en général par journée) et on calcule le nombre de journées pendant lesquelles la variable d'intérêt (par exemple le volume) a dépassé la valeur seuil choisie au moins pendant un pas de temps (c'est le raisonnement qui est utilisé pour les déversements par des déversoirs d'orage).
Soit on raisonne par événement et on calcule le nombre d'événements pour lesquels la valeur maximum de la variable d'intérêt (par exemple la valeur maximum du volume) a dépassé la valeur seuil choisie. Ce raisonnement nécessite de définir précisément comment on distingue deux événements successifs d'un événement unique avec plusieurs maximum. Ceci se fait en général en définissant une durée minimum pendant laquelle la valeur étudiée doit rester inférieure à une valeur donnée.

Il est difficile de trancher entre les deux méthodes qui présentent chacune des biais. Les deux méthodes permettent également de faire des statistiques légèrement différentes, plus faciles à exploiter en termes de période de retour ou de fréquence de dépassement (Voir : Classement fréquentiel).

[modifier] Avantages de la méthode

La méthode des débits présente le principal avantage de ne réclamer aucune condition sur la géométrie de l'ouvrage de stockage ou sur la façon dont il restitue l'eau après son stockage (les deux relations pouvant en particulier être non linéaires et dépendre du niveau de l'eau dans l'ouvrage). Il est aussi possible d'introduire des éléments de régulation en reliant $ Q_s $ au temps ou à une caractéristique de l'écoulement en un point quelconque du réseau.
La simulation continue permet de tenir compte de phénomènes ayant des dynamiques temporelles très différentes. On peut par exemple simuler la façon dont l'évapotranspiration va permettre de retrouver une capacité de stockage dans l'ouvrage en fonction de la saison, voire de la météorologie si on dispose de mesures croisées de la pluie et de l'évapotranspiration.
Ce modèle peut être couplé à des logiciels de simulation du ruissellement et éventuellement de propagation en conduites capables de produire les hydrogrammes entrant dans le bassin.
Enfin l'analyse des résultats permet d'établir des statistiques non seulement sur la hauteur d'eau dans l'ouvrage ou le volume stocké, mais également sur toutes les autres variables. Par exemple dans le cas d'un ouvrage d'infiltration avec une surverse vers un réseau, on peut faire des statistiques sur les débits surversés, voire sur les masses de polluants renvoyés au milieu naturel.

[modifier] Limites et difficultés d'utilisation

La méthode présente cependant plusieurs limites et difficultés :

Il s'agit d'une méthode de simulation et non d'une méthode de dimensionnement direct : il faut faire des hypothèses a priori sur la géométrie de l'ouvrage et sur les dispositifs de vidange avant de lancer la simulation.
La simulation d'une durée longue avec un pas de temps court peut prendre un peu de temps et nécessiter une place mémoire importante pour stocker tous les résultats (il est cependant possible de mettre en œuvre la méthode des débits en utilisant en entrée des pluies historiques ou des pluies de projet.
Les données pluviométriques utilisées (donc le pluviomètre choisi) doivent être réellement représentatives des conditions locales passées (c'est à dire sur la durée de la période de mesure de la pluie) mais également des conditions locales futures (c'est à dire sur la durée de vie de l'ouvrage projeté). Cet inconvénient existe bien sûr pour toutes les méthodes utilisables. Il doit être pris en compte de façon à ne pas surévaluer le gain en qualité de calcul par rapport à des méthodes plus simples comme la méthode des pluies ou la méthode des volumes, particulièrement à une période où le changement climatique risque de modifier le régime des pluies.
Ce type de modèle suppose qu'il ne se produit aucune propagation au sein de l'ouvrage de retenue. Cette hypothèse est tout à fait justifiée pour des bassins de retenue urbains.

@@ Ligne 1 : / Ligne 1 : @@
+[[File:logo_eurydice.jpg|80px]][[File:Logo OFB_soutien financier.png|120px]]
 ''<u>Traduction anglaise</u> : Flows design method''
-Modèle permettant de simuler le fonctionnement des ouvrages
+<u>Dernière mise à jour</u> : 31/07/2023
-de stockage ([[Bassin de retenue (HU)|bassins de retenue]]), quel que
-soit le mode de régulation des débits sortants.
-== Principe de la méthode ==
+Modèle permettant de simuler le fonctionnement des ouvrages de stockage ([[Bassin de retenue (HU)|bassins de retenue]] ou autre [[Technique alternative (HU)|technique alternative]]), quel que soit le mode de régulation des débits sortants.
-La méthode repose sur la définition de trois
+== Principes de la méthode ==
-relations :
-·
+La méthode des débits consiste à simuler en continu le fonctionnement de l'ouvrage avec un pas de temps court (de quelques minutes à quelques dizaines de minutes). La simulation est normalement faite sur une durée longue (typiquement plusieurs dizaines d'années) en utilisant en entrée une [[Chronique de pluies (HU)|chronique locale de pluies]].
-une relation de conservation des volumes :
-dVs(t)/dt
+L'application d'un [[Modèle hydrologique (HU)|modèle hydrologique]] (ou dans les cas compliqués d'un modèle de simulation plus détaillé) permet de transformer les intensités de pluie en une fonction représentant le débit entrant dans l'ouvrage en fonction du temps : <math>Q_e(t)</math>
-= Qe(t) - Qs(t)       (1)
-·
-une relation de stockage décrivant l'évolution du volume stocké Vs(t) en fonction de la hauteur d'eau
-dans le bassin, h (t) :
-Vs(t) =
+On utilise ensuite l'équation de conservation pour calculer à chaque instant la valeur du volume stocké <math>V_s(t)</math> et du débit de sortie <math>Q_s(t)</math> :
-f(h(t))                         (2)
-·
-une (ou des) relation(s) de vidange décrivant l'évolution du
-débit de sortie Qs(t) du
-bassin en fonction de la hauteur d'eau dans le bassin :
-Qs(t) =
+<center><math>\frac{dV_s(t)}{dt} = Q_e(t) - Q_s(t) \quad (1)</math></center>
-g(h(t))                        (3)
-Avec :
-·
+La résolution de cette équation est généralement faite numériquement par la  méthode des différences finies en discrétisant les différentes variables.
-Qe(t)    :  débit
-entrant dans l'ouvrage de stockage (m3/s) ;
-·
+On utilise souvent la variable intermédiaire <math>H(t)</math> qui représente la hauteur d'eau dans l'ouvrage. Les deux autres variables, <math>V_s(t)</math> et <math>Q_s(t)</math> sont en effet généralement reliées directement à <math>H(t)</math>.
-Qs(t)    :  débit
-sortant (m3/s) ;
-·
-h(t)       :  hauteur d’eau dans l’ouvrage (m) ;
-·
+* par une relation de stockage décrivant l'évolution du volume stocké <math>V_s(t)</math> en fonction de la hauteur d'eau dans le bassin, <math>h (t)</math> :
-Vs(t)    :  volume
-stocké dans l'ouvrage (m3).
+<center><math>V_s(t) = f \lgroup h(t)\rgroup \quad (2)</math></center>
+* par une (ou des) relation(s) de vidange décrivant l'évolution du débit de sortie <math>Q_s(t)</math> du bassin en fonction de la hauteur d'eau dans le bassin :
+<center><math>Q_s(t) = g \lgroup h(t)\rgroup \quad (3)</math></center>
+Avec :
+* <math>Qe(t</math>) : débit entrant dans l'ouvrage de stockage (m<sup>3</sup>/s) ;
+* <math>Qs(t)</math> : débit sortant (m<sup>3</sup>/s) ;
+* <math>h(t)</math> : hauteur d’eau dans l’ouvrage (m) ;
+* <math>Vs(t)</math> : volume stocké dans l'ouvrage (m<sup>3</sup>).
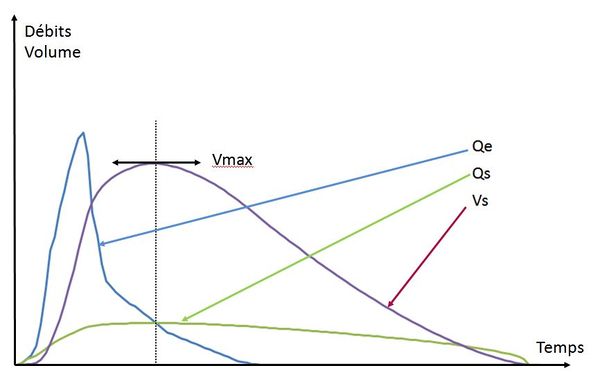
-La hauteur d'eau stockée dans le bassin et le débit sortant
+La hauteur d'eau et le volume stocké dans le bassin ainsi que le débit sortant peuvent alors être calculés en fonction du temps, en résolvant numériquement le système constitué par les équations (1), (2) et (3) et il est possible de déduire la valeur du volume stocké maximum (<math>Vmax</math>) pour chaque événement simulé (''figure 1'').
-peuvent alors être calculés en fonction du temps, en résolvant numériquement le
-système constitué par les équations (1), (2) et (3).
+[[File:methode des débits.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Évolution des différentes grandeurs en fonction du temps pour un événement pluvieux donné.''</center>]]
-<center>[[Fichier:DEHUA126.png]]</center>
+== Analyse des résultats ==
+Cette simulation produit en sortie des chroniques de hauteurs d'eau, de débits de sortie et de volumes stockés, associées au pas de temps de calcul choisi.
+On peut donc facilement compter le nombre de valeurs qui, pour la variable d'intérêt, dépassent un seuil donné et en déduire la durée de dépassement pendant la durée de simulation. On peut par exemple calculer le nombre de pas de temps pendant lequel (c'est à dire la durée totale pendant laquelle) le volume à stocker a été supérieur à une valeur donnée.
+Ce résultat est cependant difficilement exploitable en termes de fréquence de dépassement (ou de [[Période de retour (HU)|période de retour]]) car il mélange deux notions différentes : le nombre de fois ou le volume à dépassé la valeur choisie et la durée de chacun des dépassements. Pour éviter cet inconvénient il est donc nécessaire de compléter le raisonnement, ce qui peut se faire de deux façons différentes :
+* Soit on raisonne par période temporelle (en général par journée) et on calcule le nombre de journées pendant lesquelles la variable d'intérêt (par exemple le volume) a dépassé la valeur seuil choisie au moins pendant un pas de temps (c'est le raisonnement qui est utilisé pour les déversements par des déversoirs d'orage).
+* Soit on raisonne par événement et on calcule le nombre d'événements pour lesquels la valeur maximum de la variable d'intérêt (par exemple la valeur maximum du volume) a dépassé la valeur seuil choisie. Ce raisonnement nécessite de définir précisément comment on distingue deux événements successifs d'un événement unique avec plusieurs maximum. Ceci se fait en général en définissant une durée minimum pendant laquelle la valeur étudiée doit rester inférieure à une valeur donnée.
-Evolution des différentes grandeurs en fonction du
+Il est difficile de trancher entre les deux méthodes qui présentent chacune des biais. Les deux méthodes permettent également de faire des statistiques légèrement différentes, plus faciles à exploiter en termes de période de retour ou de fréquence de dépassement (Voir : [[Classement fréquentiel (HU)|Classement fréquentiel]]).
-temps.
-== Hypothèses et limites d'utilisation ==
+== Avantages de la méthode ==
-Ce type de modèle suppose qu'il ne se produit aucune
+* La méthode des débits présente le principal avantage de ne réclamer aucune condition sur la géométrie de l'ouvrage de stockage ou sur la façon dont il restitue l'eau après son stockage (les deux relations pouvant en particulier être non linéaires et dépendre du niveau de l'eau dans l'ouvrage). Il est aussi possible d'introduire des éléments de régulation en reliant <math>Q_s</math> au temps ou à une caractéristique de l'écoulement en un point quelconque du réseau.
-propagation au sein de l'ouvrage de retenue. Cette hypothèse est tout à fait
+* La simulation continue permet de tenir compte de phénomènes ayant des dynamiques temporelles très différentes. On peut par exemple simuler la façon dont l'[[Evapotranspiration (HU)|évapotranspiration]] va permettre de retrouver une capacité de stockage dans l'ouvrage en fonction de la saison, voire de la météorologie si on dispose de mesures croisées de la pluie et de l'évapotranspiration.
-justifiée pour des bassins de retenue urbains.
+* Ce modèle peut être couplé à des logiciels de simulation du ruissellement et éventuellement de propagation en conduites capables de produire les [[Hydrogramme (HU)|hydrogrammes]] entrant dans le bassin.
+* Enfin l'analyse des résultats permet d'établir des statistiques non seulement sur la hauteur d'eau dans l'ouvrage ou le volume stocké, mais également sur toutes les autres variables. Par exemple dans le cas d'un ouvrage d'infiltration avec une surverse vers un réseau, on peut faire des statistiques sur les débits surversés, voire sur les masses de polluants renvoyés au milieu naturel.
-Ce modèle nécessite d'être couplé à des logiciels de
+== Limites et difficultés d'utilisation ==
-simulation du ruissellement et éventuellement de propagation en conduite
-capables de produire les [[Hydrogramme (HU)|hydrogrammes]]
-entrants dans le bassin pour des [[Pluie de projet (HU)|pluies de
-projet]], ou, de façon préférable, pour des périodes de
-temps assez longues incluant des événements forts (plusieurs dizaines d’années
-si possible).
-L'une des difficultés d'application de ce modèle réside dans
+La méthode présente cependant plusieurs limites et difficultés :
-la détermination de la loi de vidange pour des ouvrages de sortie complexe.
+* Il s'agit d'une méthode de simulation et non d'une méthode de dimensionnement direct : il faut faire des hypothèses a priori sur la géométrie de l'ouvrage et sur les dispositifs de vidange avant de lancer la simulation.
-Cette difficulté n'existe cependant pas dans les études de conception où l'on
+* La simulation d'une durée longue avec un pas de temps court peut prendre un peu de temps et nécessiter une place mémoire importante pour stocker tous les résultats (il est cependant possible de mettre en œuvre la méthode des débits en utilisant en entrée des [[Pluie historique (HU)|pluies historiques]] ou des [[Pluie de projet (HU)|pluies de projet]].
-fait des hypothèses simplificatrices (débit constant, simple surverse, vidange
+* Les données pluviométriques utilisées (donc le pluviomètre choisi) doivent être réellement représentatives des conditions locales passées (c'est à dire sur la durée de la période de mesure de la pluie) mais également des conditions locales futures (c'est à dire sur la durée de vie de l'ouvrage projeté). Cet inconvénient existe bien sûr pour toutes les méthodes utilisables. Il doit être pris en compte de façon à ne pas surévaluer le gain en qualité de calcul par rapport à des méthodes plus simples comme la [[Méthode des pluies (HU)|méthode des pluies]] ou la [[Méthode des volumes (HU)|méthode des volumes]], particulièrement à une période où le [[Changement climatique (HU)|changement climatique]] risque de modifier le régime des pluies.
-par orifice, etc.). Il est aussi possible d'introduire des éléments de
+* Ce type de modèle suppose qu'il ne se produit aucune propagation au sein de l'ouvrage de retenue. Cette hypothèse est tout à fait justifiée pour des bassins de retenue urbains.
-régulation en reliant Qs au
-temps ou à une caractéristique de l'écoulement en un point quelconque du
-réseau. Voir aussi [[Méthode des pluies (HU)|Méthode des pluies]], [[Méthode des volumes (HU)|Méthode des volumes]].
-[[Catégorie:Dictionnaire DEHUA]]
+[[Catégorie:Dictionnaire_DEHUA]]
+[[Catégorie:Solutions_alternatives_et_compensatoires_(HU)]]
+[[Catégorie:Dimensionnement_des_ouvrages_de_stockage_(HU)]]
+[[Catégorie:Modélisation_des_écoulements_en_réseau_et_en_rivière_(HU)]]