Prévision des crues : les modèles utilisés (HU) : Différence entre versions

Version du 9 mai 2024 à 17:26

Traduction anglaise : Models used for flood forecasting

Dernière mise à jour : 09/05/2024

article en chantier

Cet article a pour objectif de présenter les différents modèles qui sont utilisés en France pour la prévision des crues.

Il a bénéficié de la relecture et des contributions de Renaud Marty et de Pierre-Adrien Hans (tous deux du SPC Loire-Allier-Cher-Indre), de Charles Perrin (INRAE-HYCAR, à Antony), Etienne Le Pape et Didier Narbaïs-Jauréguy (tous deux du SCHAPI).

Introduction

Cet article fait partie d'une série de sept articles qui traitent des différents aspects de la prévision des crues, un article général :

• Prévision des crues et des inondations : vue globale (HU) ;

et 5 autres articles détaillant différents aspects (actuellement en cours d'écriture) :

• Prévision des crues : son historique en France ;
• Prévisions des crues : les données nécessaires ;
• Prévisions des crues : erreurs, incertitudes et évaluation des performances ;
• Prévision des crues : les outils opérationnels utilisés en France ;
• Prévision des crues : développements récents ou en cours en France.

Cet article fait également référence à une partie des fiches de la famille « B. Description des principales sources d’incertitudes à considérer dans l’élaboration [par modélisation] d’une prévision de débit et de hauteur d’eau » Ces fiches ont été élaborées entre 2013 et 2015 par un groupe de travail constitué de prévisionnistes des SPC et du SCHAPI, ainsi que de confrères de Météo-France, de l’IRSTEA (devenu INRAE) et de l’IFSTTAR (devenu Université Gustave Eiffel). En effet, ces fiches, pour présenter les incertitudes liées aux données utilisées et modèles eux-mêmes, décrivent assez précisément les processus qu’ils mettent en œuvre.

Il traite successivement :

• des divers types de modèles utilisés par le réseau national français pour la prévision des crues ;
• des modèles hydrologiques, simulant la relation entre la pluie précipitée sur les bassins versants élémentaires et les débits à leur exutoire (où ils sont « injectés » dans le réseau hydrographique principal et modélisé) ;
• des modèles hydrauliques (ou hydrodynamiques), simulant la propagation des ondes de les 2crues et leurs compositions aux confluences, dans le réseau hydrographique modélisé.

Les modèles, hydrologiques et hydrauliques, y sont présentés suivant un schéma similaire :

• les fonctions et les limites de ces modèles,
• les divers types de modèles utilisés pour la prévision, et ceux qui ont été choisis pour un soutien prioritaire aux développements et pour l’aide à leur maîtrise, faits dans le cadre de la stratégie du réseau national français pour la prévision des crues,
• des points d’attention majeurs pour la construction et l’utilisation de ces modèles,
• des cas particuliers.

Présentation générale des modèles utilisés pour la prévision des crues

Les modèles utilisés pour la prévision des crues ont pour fonction de prévoir l'évolution des débits (et des lignes d'eau dans le cas de la prévision des inondations) sur le linéaire d'un cours d'eau lors d'un événement pluvieux. Comme pour de nombreuses autres applications en hydrologie, ils sont le plus souvent de type semi-distribué, c'est à dire que le territoire d'étude est décomposé en sous-bassins versants qui produisent des débits en fonction des précipitations qu'ils reçoivent, ces sous-bassins versants étant connectés entre eux par des tronçons de rivière (et éventuellement des ouvrages de stockage). Ils reposent donc sur deux catégories distinctes de modèles qui doivent être utilisés de façon conjointe :

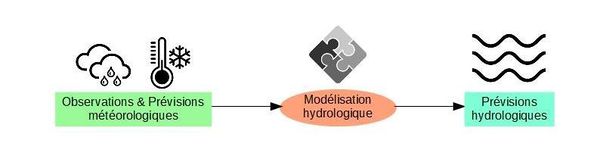
• les modèles hydrologiques qui simulent la transformation des variables météorologiques (en particulier des précipitations) ou hydrologiques antérieures, en variables débitmétriques à l'exutoire des bassins versants ; ils sont alimentés par les observations et les prévisions météorologiques et sont chargés de prévoir les valeurs de débit qui vont s'écouler dans les cours d'eau aval (figure 1) ;
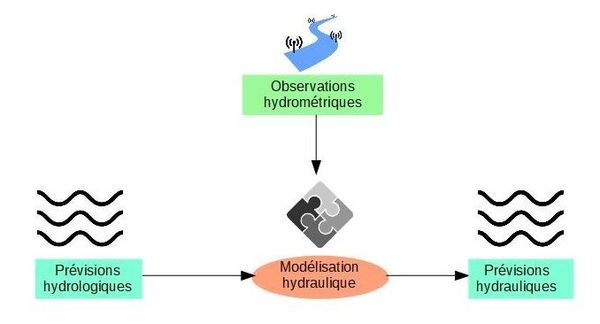
• les modèles hydrauliques (ou hydrodynamiques), ou leurs versions simplifiées qui simulent uniquement la propagation des ondes de crues (comprenant les phénomènes de déplacement de ces ondes et d’amortissement-stockage intermédiaire, voir Modèle de propagation d’ondes de crue (HU)) ; ces modèles sont chargés de représenter l'évolution prévue des débits, des hauteurs d'eau et des vitesses dans les lits mineurs, moyens ou majeurs des cours d’eau modélisés, ainsi que la composition des ondes de crue aux confluences et, éventuellement, leur transformation dans les retenues ou d’autres phénomènes d’hydraulique influencée, comme en zone fluviomaritime ou en amont de certaines confluences (voir Modèles d'écoulement en réseau et en rivière (HU)) ; ils sont alimentés par les prévisions issues des modèles hydrologiques, les résultats simulés étant éventuellement corrigés par des observations hydrométriques (figure 2).

Figure 1 : Illustration schématique d’une chaîne de prévision hydrologique sur un bassin versant ; les observations météorologiques sont formulées en valeur instantanée pour la température et en moyennes sur un pas de temps des intensités de pluie (mm/h) et des observations et prévision hydrologiques en débit (m3/s) ; Source : Marty, 2020.

Figure 2 : Illustration schématique d’une chaîne de prévision hydraulique sur un tronçon de cours d’eau pour représenter la propagation d’une onde de crue : les « entrées » du modèles sont constituées : des observations hydrométriques, en amont du tronçon sur le cours d’eau principal ainsi que sur les affluents ; des prévisions hydrologiques à l’exutoire des bassins versants « élémentaires » situés immédiatement en amont du tronçon ; de l’estimation des apports hydrologiques intermédiaires entre points d’injection des apports de ces bassins versants « élémentaires ou entre 2 stations hydrométriques ; et des prévision hydrauliques ; Source : Marty, 2020.

Deux familles de modèles sont utilisées en prévision des crues :

• des modèles événementiels. : leur objectif est de simuler les crues résultant d’un évènement pluvieux particulier ou d’une série de pluies suffisamment rapprochées pour générer des ruissellements qui interfèrent entre eux, ce qui justifie que l'on considère la crue de façon globale ; ces modèles sont souvent limités par la difficulté à déterminer pour eux des conditions initiales fiables, ce qui conduit par exemple à les coupler avec des modèles continus (ils sont de moins en moins souvent utilisés seuls) ou à anticiper leur mise en route par une phase de « chauffe » ;
• des modèles continus : ces modèles prennent en compte en continu toutes les précipitations qui se succèdent sur le bassin hydrographique durant une longue période (base annuelle glissante). Ils permettent de connaître les variables (comme l’humidité du sol) qui dépendent à la fois de l'antécédent pluviométrique, des conditions météorologiques, de la succession des saisons. Ils sont utiles notamment pour déterminer les conditions initiales nécessaires aux modèles événementiels, hydrologiques mais aussi hydrauliques.

Nota : Il existe dans la littérature plusieurs typologies des modèles. On peut s’appuyer en partie sur celles de (Todini, 2007) et de (Roche et al., 2012) au Chapitre 10.3, ou de (Le Pape, 2020). On distingue par exemple souvent : les modèles empiriques (basés sur l’expérience et les données d’observation disponibles), les modèles conceptuels et les modèles à base physique. Les frontières entre ces catégories ne sont pas toujours très nettes et plusieurs modèles peuvent être considérés comme hybrides. Nous renvoyons le lecteur à l'article Modèle (HU) pour en savoir plus sur les différentes classifications possibles.

Rapide historique des modèles de plus en plus élaborés utilisés en France pour la prévision des crues

Les premières prévisions des crues modernes et structurées ont été faites en France à partir du milieu du XIXe siècle (Voir l'article Prévision des crues : son historique en France), après les crues de 1840 sur le Rhône et de 1846 sur la Loire, en élaborant des combinaisons linéaires des hauteurs d’eau relevées sur des échelles en amont, en des points choisis pour représenter au mieux la réaction de parties assez homogènes (en pédologie, géologie et topographie). Elles ont été élaborées pour évaluer le niveau maximum à attendre et le moment où il se produira plus en aval, au droit de zones particulièrement vulnérables aux inondations.

Malgré la proposition, dès 1871 par Adhémar Barré de Saint-Venant, d’un système d'équations différentielles décrivant la propagation des ondes de crues dans les cours d’eau, ainsi que des compléments apportés par d’autres dans les années suivantes, ces équations n’ont pas eu de suites pratiques pendant près d’un siècle, faute de moyens pour les résoudre aisément, avant l’avènement de l’informatique.

En 1934 pour la prévision des crues de la Loire de Gien à Montjean, puis en 1940 et en 1948 (Bachet, 1948) propose une méthode, pouvant aussi être qualifiée de modèle, traduite, notamment pour compenser un peu des pertes de compétences, par un ingénieux jeu d’abaques, les « Réglettes de Bachet », longtemps utilisées dans plusieurs Services d’Annonce des Crues (figure 3). (Voir Fiche B.23 – Modèles hydrologiques empiriques).

Figure 3 : Exemple de réglette de Bachet dans le bassin de la Garonne : la prévision à la station de LAMAGISTERE se fait à partir de deux stations : VERDUN et SAINT-SULPICE ; Source : Ntonga, 1984.

En parallèle, dans les années 1930, on voit apparaître la notion de modèles numériques, essentiellement hydrauliques, conceptuels ou simplifiant les équations de Barré de Saint-Venant, qui seront utilisés plus tard pour expliquer, représenter à des fins d’aménagement et prévoir la propagation des crues. A partir des années 1960, à titre expérimental (Cunge, 2020), puis plus opérationnel, et de façon largement dominante depuis le début des années 2010, les modèles hydrologiques et hydrauliques (ou hydrodynamiques) numériques sont les outils utilisés pour la prévision des crues.

La généralisation relativement rapide, en une dizaine d’années, de l’utilisation de modèles numériques de prévision des crues est le résultat de plusieurs facteurs :

• la maturation antérieure sur la modélisation hydrologique et hydraulique au niveau de certaines Directions régionales de l’environnement (DIREN) qui avaient eu recours à de tels modèles pour les Plans Grands Fleuves (Loire, Rhône, Seine, etc.) ou pour consolider, avec les Directions départementales de l’Équipement puis des Territoires (et de la Mer), les Plans de Prévention des Risques d’Inondation (PPRI) ;
• la création en 2002 des Services de Prévision des Crues (SPC), dont une majorité au sein des DIREN, avec l’affichage de l’ambition d’une prévision des crues allant au-delà de leur annonce (comme auparavant), et l’invitation, ensuite, à publier de plus en plus sur le site Vigicrues ces prévisions ainsi que les incertitudes associées ;
• le fonctionnement en réseau des SPC et du SCHAPI, créé en 2003, avec des échanges renforcés et des formations structurées ;
• l’établissement de relations fortes, avec un soutien financier croissant, entre le SCHAPI, et les SPC, d’une part, et les milieux de la recherche et des développements, d’autre part ;
• la mise à disposition progressive de données nécessaires (pluviométriques et radar-météorologiques ; humidité des sols calculée par Météo-France ; possibilité de relevés topographiques suffisamment précis, par GPS puis aussi par LIDAR aéroporté, réalisés depuis 2011 sur la quasi-totalité des zones inondables par les cours d’eau du réseau hydrographique surveillé par l’État ;
• l’organisation de Retours d’expérience (REX) des évènements marquants en matière d’importance des dommages mais aussi d’enseignements à tirer dans le processus de prévision, notamment d’améliorations souhaitables des modèles ; le dispositif de collaboration continue avec les équipes de recherche et développement impliquées dans ceux-ci permet de dégager assez rapidement des évaluations des performances et des perspectives d’améliorations ciblées : on peut citer, par exemple, le travail mené par l’Equipe HYDRO (UR HYCAR) de l’INRAE, concernant le modèle GRP, par suite des importants inondations de mai-juin 2016 ayant touché le bassin de la Seine et le nord de celui de la Loire (Pinna, 2017), et l’analyse par suite de la crue de février 2021 sur la Garonne marmandaise (Marchandise et al., 2023) ou celle des crues de juillet 2021 sur les bassins du nord-est de la France (Diederics et al, 2023).

Modèles hydrologiques

Fonctions et limites des modèles hydrologiques

Dans le cadre de la prévision des crues, les modèles hydrologiques visent à estimer les valeurs futures, à divers horizons de prévision, que va prendre le débit à l’exutoire des bassins versants.

Les modèles utilisés prennent en compte les données acquises en cours d’évènement concernant la pluie que le bassin versant a reçue ou qu’il est prévu qu’il recevra, ainsi que des paramètres variables en fonction de l’antécédent pluviométrique (humidité des sols, éventuellement niveau des nappes, etc.). Ils utilisent aussi comme donnée de référence, lorsque c’est possible, le débit ou le niveau du cours d’eau constituant le drain final du bassin versant modélisé.

Les bassins versants sont des systèmes très complexes dont on ne peut cerner qu’une partie de la réalité. Il est donc nécessaire de s’appuyer sur un certain nombre d’hypothèses, pas toujours vérifiées ; de plus, certaines données ne sont pas accessibles en temps réel. Comme pour la plupart de ceux qui représentent des systèmes environnementaux complexes, on ne peut donc pas attendre que ces modèles donnent des résultats très précis. Pour en savoir plus sur les incertitudes associées à ce type de modélisation, voir la fiche B.18 – Modélisation hydrologique : quelles incertitudes ?

Les modèles hydrologiques utilisés pour la prévision des crues et ceux qui ont été choisis pour un soutien prioritaire aux développements et pour l’aide à leur maîtrise

Modèles hydrologiques utilisés en France et dans le monde pour la prévision des crues

Les modèles hydrologiques anciennement et actuellement utilisés dans le réseau pour la prévision des crues en France sont :

• les modèles conceptuels à réservoirs, évènementiels au départ puis utilisables aussi en continu, de la famille GR développés par l’INRAE (ex-CEMAGREF et IRSTEA) : GR3H (utilisé dans la plate-forme SOPHIE), GR4H à la fin des années 2000 (au SPC LCI) puis à partir du début des années 2010, les versions successives du modèle GRP ;
• les modèles hydrologiques évènementiels et géographiquement distribués, à base relativement physique, de la plate-forme PLATHYNES, utilisée pour leur calage et leur utilisation en temps réel ; PLATHYNES résulte de la fusion, en 2014, des plates-formes ATHYS et MARINE ; le modèle ALTHAIR, développé et utilisé depuis le début des années 2000 par le Service de Prévision des Crues - SPC - Grand Delta [du Rhône] pour la prévision des crues rapides voire soudaines sur son territoire , après des efforts de spatialisation de ce modèle en 2005 (Ayral et al., 2005), a été porté sur PLATHYNES, aussi en 2014 ;
• le modèle LARSIM - Large Area Runoff SImulation Model -, géographiquement distribué, et développé par la Communauté des développeurs de LARSIM (LARSIM, 2019), (Bourcet, 2013) et utilisé sur l’ensemble du bassin du Rhin, en particulier en France sur les bassins de la Moselle ainsi que du Rhin et de la Sarre, dans le cadre d’un système transfrontalier partagé de prévision des crues côtés français, luxembourgeois, et, en Allemagne, sarrois et rhénano-palatins ; il est aussi utilisé pour le bassin versant de la Meuse. Il s’applique à des mailles de 1km x 1km ou par sous-bassins versants, dit « de bilan hydrologique » (où est simulée une série assez complète des sous-processus hydrologiques) ;
• le modèle MORDOR de prévision des crues et des étiages, développé par EDF depuis le début des années 1990 (Paquet, 2004). Il n’est utilisé jusqu’ici que marginalement par le réseau Vigicrues ;
• pour l’anticipation des crues soudaines, le modèle SMASH (anciennement AÏGA), mis en œuvre dans Vigicrues Flash (Voir Vigicrues Flash (HU).

On peut aussi citer, entre beaucoup d’autres utilisés au niveau mondial, les modules hydrologiques des plates-formes de modélisation suivantes, incluant des fonctions de prévision, qui sont, ou ont pu être, mis en œuvre en France :

• HYDRA (SETEC / Hydratec), géographiquement semi-distribué, pour l’hydrologie ;
• Delft FEWS – Hydrological Forecasting and Warning System – (Deltares aux Pays-Bas) ;
• La plate-forme LISFLOOD, base du système EFAS, conçue par le Centre commun de recherche (JRC) de la commission européenne pour les bassins fluviaux internationaux par suite des inondations de l’Oder, de l’Elbe et du Danube en 1997 et après ; il utilise le modèle LISFLOOD (Van Der Knijff et al., 2008), géographiquement distribué à base physique et utilisant des fonctions géomatiques ;
• HEC-HMS, géographiquement distribué, développé par l’Hydrologic Engineering Center of the US Army Corps of Engineers - USACE-, HMS signifiant Hydrologic Modelling System, basé sur les principes des modèles SCS (développés par le Soil Conservation Service américain depuis la fin des années 1960 ; il peut alimenter divers modèles hydrauliques, dont HEC-RAS.

Les modèles hydrologiques priorisés dans le réseau Vigicrues

Le réseau national pour la prévision des crues, sous l’impulsion du SCHAPI, a préparé dès 2010 (Le Pape et Souldadié, 2010), puis adopté en 2012, une stratégie de développement et de consolidation des modèles hydrologiques et hydrauliques de prévision, qui a été ensuite régulièrement actualisée, notamment en 2020. Cette stratégie est centrée sur des modèles :

• remplissant divers critères (ouverture des codes informatiques, gratuité, existence d’une communauté de développeurs et utilisateurs, etc.) ;
• s’avérant pertinents ;
• restant suffisamment peu nombreux pour bénéficier d’un soutien suffisant pour leurs développements et l’aide à leur maîtrise, y compris par la formation.

De plus, la stratégie prévoit, pour les modèles hydrologiques, de :

• s’appuyer sur les outils existants tant qu’ils donnent satisfaction et ne sont pas remplacés par d’autres plus performants en s'appuyant notamment sur SOPHIE, une plate-forme multi-modèles « pluie-débit » ou « débit-débit », développée en France dès les années 1980 (Roche et al. , 2012), (voir aussi B.23 - Modèles hydrologiques empiriques) et qui a été utilisée comme pilote d’une structure plus complète, la Plate-forme opérationnelle pour la modélisation, la POM, qui l’a remplacée. Les formules ou modèles qu’elle mettait en œuvre ont pour la plupart été abandonnés ;
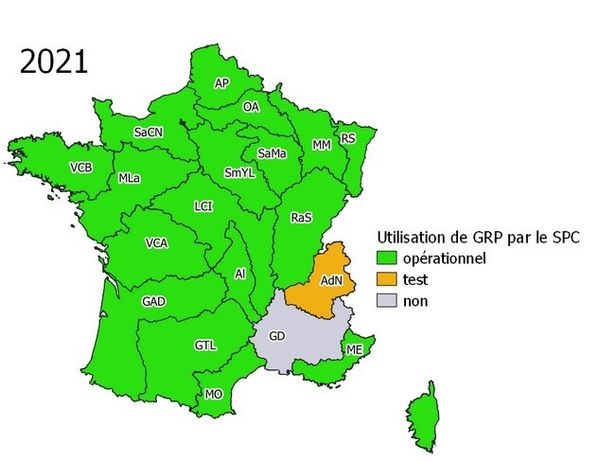
• installer très largement le modèle GRP, relativement simple et robuste, dans tous les cas où il s’avère qu’il donne satisfaction (figure 4) ;
• soutenir le développement des modèles distribués empiriques et à base relativement physique, en favorisant leur convergence (dans le cadre de la plate-forme PLATHYNES) en privilégiant, au départ, leur utilisation dans des cas de bassins versants à caractéristiques très contrastées et où les crues sont souvent consécutives à des évènements pluvieux très hétérogènes voire, comme on le verra plus loin, pour des sous-bassins versants non jaugés, ou pour mieux évaluer des apports intermédiaires entre stations de mesure. L’observation, au cours de ces dernières années d’événements pluvieux localisés et intenses sur des territoires peu habitués à ce genre d’épisodes a conduit à la mise en œuvre de modèles distribués en compléments des approches globales traditionnelles ;
• développer des stratégies de modélisation sur sites non jaugés, dans le cadre des évolutions de Vigicrues Flash et de la plate-forme PLATHYNES.

Figure 4 : Utilisation en 2021 du modèle GRP dans les SPC en France ; Source : : https://webgr.inrae.fr/outils/modeles-hydrologiques/modele-de-prevision-hydrologique-grp.

Des points d’attention majeurs pour la construction et l’utilisation des modèles hydrologiques conceptuels de prévision des crues : exemple de GRP

Le calage de ces modèles hydrologiques : exemple de GRP

On pourra se référer notamment à la Fiche B.19 - Calage des modèles hydrologiques de la Catégorie:Incertitudes, ainsi que, pour GRP, à (Tangara, 2005) et à (Berthet, 2010).

Le calage des modèles hydrologiques est indispensable, qu’ils aient ou non une part de signification physique, plus ou moins mesurable. Ce calage, du fait que ces paramètres représentent la particularité de chaque bassin versant, doit s’appliquer à chacun d’eux. Il consiste à :

• analyser et critiquer (ou utiliser des séries déjà validées) les données d’évolution dans le temps :
  • d’intensité de pluie précipitée sur le bassin versant (données d’entrée du modèle),
  • et de débit à l’exutoire de celui-ci (données de sortie du modèle),

pour un échantillon de crues continu aussi long que possible et comprenant de préférence des évènements de période de retour statistique assez longue ;

• ajuster (phase d’apprentissage), sur une partie de l’échantillon, la valeur de ces paramètres, en minimisant les écarts entre les débits prévus à l’exutoire par le modèle et les débits observés, en mettant en œuvre une fonction objectif utilisant des critères de calage, comme ceux de Nash-Sutcliffe (Nash and Sutcliffe, 1970) ou Kling-Gupta (Gupta et al., 2009) ou d’autres ;
• et valider ces paramètres, sur une autre partie de l’échantillon, pouvant correspondre en partie à des contextes différents.

Les calages, pour certains modèles, comme pour ceux de la famille GR développés par l’Unité HYCAR de l’INRAE, et donc le modèle GRP, peuvent être semi-automatisés grâce aux fonctionnalités d’un utilitaire de calage et d’évaluation (Furusho et al., 2014).

Par exemple, dans le cas du modèle GRP (figure 5), trois paramètres, dits libres font l’objet d’un calage :

• Corr : sans unité, en phase finale du module de production, facteur de correction du volume total de pluie efficace Pr, pour donner P’r, la pluie efficace corrigée alimentant le module de routage, qui répartit temporellement celle-ci ;
• TB : le temps de base de l’hydrogramme unitaire (en nombre de pas de temps) qui permet de simuler le décalage temporel entre la pluie précipitée sur le bassin versant et le débit à son exutoire ;
• Rout : la capacité (en mm/pas de temps) du réservoir de transfert (l’autre module central de GRP), qui assure un lissage temporel de la pluie efficace corrigée

Figure 5 : Schéma structurel du modèle GRP (E : ETP ; P : pluie ; Q : débit ; CORR (-) : facteur de correction des pluies efficaces ; TB (h) : temps de base de l’hydrogramme unitaire ; ROUT (mm) : capacité du réservoir de routage ; les autres lettres représentent des variables internes) ; Source : Lilas et al (2012).

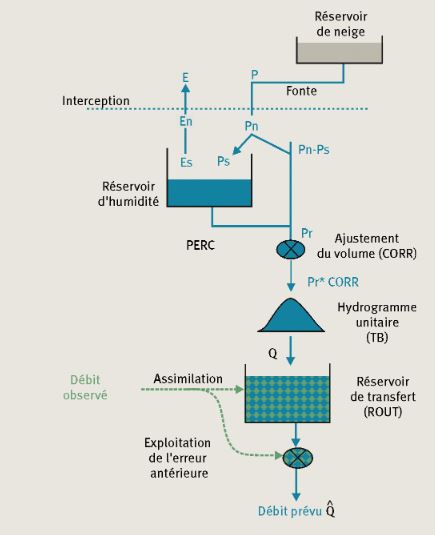
Il est à noter que :

• la pluie précipitée a le statut de donnée d’entrée (ou de forçage) et le volume du réservoir d’humidité (dans le module de production) est initialisé comme on le verra au § 3.3.2. ci-dessous ;
• le modèle comporte, en amont dans les processus modélisés, deux modules récents, devant être initialisés :
  • un module neige qui est dédié à l’accumulation et à la fonte de la neige,
  • ainsi qu’un réservoir d’interception des précipitations par l’évapotranspiration potentielle ;
• en aval dans ce processus, une procédure d’assimilation des valeurs du dernier débit observé et de l’écart entre celui qui avait été prévu et celui qui a été observé au pas de temps précédent, permet de corriger les valeurs aux pas de temps suivants de la capacité du réservoir de routage ; cette assimilation requiert donc une 3ème donnée d’entrée, le dernier débit observé à l’exutoire. Cette procédure est à utiliser préférentiellement en mode opérationnel de prévision, car en calage elle peut influencer la détermination des paramètres du modèle (Astagneau, 2022) ; une réflexion est en cours pour atténuer, si possible, cet inconvénient.

L’initialisation de ces modèles

On pourra aussi se référer notamment à la Fiche B.24 - Initialisation des modèles hydrologiques et incertitude résultante de la Catégorie:Incertitudes, dans Wikhydro.

Lors de l’initialisation d’un modèle hydrologique, on définit la valeur des variables d’état au démarrage d’une période de prévision (ou d’un autre type de simulation), pour décrire l’état du système hydrologique (bassin versant, y compris les cours d’eau qui le drainent) à ce moment-là. La précision des prévisions dépend beaucoup de la qualité de l’initialisation : notamment, celle des variables d’état traduisant l’humidité du sol au début de l’évènement, car elle a une forte influence sur les valeurs du débit simulé.

Pour initialiser un modèle, on peut avoir recours à trois méthodes :

• l’observation des débits à l’exutoire du bassin versant, qui peuvent être des témoins de l’état d’humidité des sols, comme dans une procédure d’assimilation des données ;
• ou l’initialisation évènementielle, en s’appuyant sur des indicateurs calculés comme ceux de la chaîne SIM (Safran – Isba – Modcou) (https://www.umr-cnrm.fr/spip.php?article424) puis d’ISBA-CTRIP (https://www.umr-cnrm.fr/spip.php?article1092) mis à disposition du SCHAPI et des SPC par Météo-France ; l’initialisation par l’indicateur HU d’humidité des sols issu de ces chaînes est opérationnelle depuis la fin 2023 pour les modèles de la plate-forme PLATHYNES ainsi que pour des abaques de vigilance utilisés par certains SPC, d’autres se référant aussi, comme témoins, aux débits observés à l’aval des bassins versants concernés ; même pour un prévisionniste averti il s’avère difficile, en particulier pour les modèles conceptuels, de relier un certain nombre de variables d’état à des observations disponibles en temps réel car elles peuvent varier sensiblement suivant leur localisation et les évolutions météorologiques ;
• ou la simulation continue de l’historique des pluies et des évènements de temps sec pendant une assez longue période avant l’évènement faisant l’objet de la prévision. Cela demande de disposer d’une version adaptée du modèle, qui s’appuiera sur les mesures de pluie (et, si on est en mode « assimilation », sur celles du débit à l’exutoire), ainsi que de mesures météorologiques complémentaires. Pour la plupart des modèles hydrologiques, les résultats d’une simulation continue assez longue deviennent assez indépendants des variables d’état initiales : il est conseillé, pour le modèle GRP, de simuler en mode continu une période d’une année, ou moins, mais en prenant des précautions particulières.

Le fonctionnement en extrapolation de ces modèles

On pourra aussi se référer notamment à la Fiche B.20 - Modélisation hydrologique : fonctionnement en extrapolation de la Catégorie:Incertitudes, dans Wikhydro.

Un modèle fonctionne en extrapolation lorsqu’il s’applique à des pluies ou des débits dont les caractéristiques sortent de la gamme de ceux sur lesquels il a été calé. Ces caractéristiques peuvent être les valeurs très fortes d’intensité de pluie ou de débit maximal, correspondant à des évènements assez rares et dont on n’aura pas toujours la chance de disposer dans l’échantillon des données observées, qui sont souvent des séries de seulement quelques dizaines d’années ou moins, alors que les périodes de retour statistique des crues les plus destructrices sont plus importantes ; elles peuvent aussi concerner des situations surprenantes non observées sur l’échantillon, comme des ruissellements très fortement ou faiblement amortis au regard des caractéristiques des précipitations.

Les modèles qui respectent des principes robustes, comme la conservation de la masse, le garde-fou le plus fiable, sont moins susceptibles de donner, en extrapolation, des résultats trop faux. Les modèles conceptuels prenant cette précaution, ou les modèles à base physique, sont en général dans ce cas, contrairement aux réseaux de neurones artificiels ou à des modèles empiriques, en particulier certains de ceux qui ont été mis en œuvre dans la plate-forme multi-modèles SOPHIE et qui ont qui ont été repris dans PLATHYNES, comme les modèles de « relations linéaires ».

Les améliorations récentes ou envisagées du modèle GRP

Le pas de temps de calcul doit être ajusté en fonction de la réactivité du bassin versant : si le décalage temporel entre la pluie et le débit à l’exutoire est relativement faible, de quelques dizaines de minutes, un modèle à pas de temps horaire, comme GRP initialement, risque de ne rendre compte des phénomènes que de manière assez grossière, tendant notamment à sous-estimer les débits de pointe. Mais la structure du modèle est dépendante du pas de temps, dont la modification ne peut pas se réaliser sans adapter cette structure et vérifier que cela n’altère pas les performances à attendre. Des travaux ont été engagés en ce sens, par exemple, pour augmenter la flexibilité temporelle du modèle GRP (Viatgé, 2019) (Ficchi, 2017). Il s’en est suivi le développement d’une structure multi-pas de de temps infra-horaires, rendue opérationnelle en 2019.

De plus, d’autres travaux ont été engagés par suite des retours d’expérience, concernant notamment le modèle GRP, sur les inondations de 2013 et janvier 2014 dans le sud-est de la France, ainsi que de mai-juin 2016 sur le bassin de la Seine et le nord du bassin de la Loire :

• Une première analyse, menée dans le cadre d’un mémoire de Master 2 (Pinna, 2017), est centrée sur le constat que :
  • la valeur des débits maximaux au pic de crue peut être assez largement sous-estimée, et pas seulement du fait que le pas de temps horaire peut être trop long,
  • une réponse un peu « molle » du modèle pour reproduire certaines « montées » d’hydrogramme, se traduisant par un retard de celle-ci et dans le positionnement temporel des pics de crue.

Les investigations sur l’origine de ces insuffisances ont porté prioritairement sur la structure du modèle et les stratégies pour son calage, en ne perdant pas de vue qu’il faudra aussi regarder de près le rôle que peut jouer le processus d’assimilation de données.

Elles ont débouché sur l’élaboration de versions de GRP potentiellement utilisables en mode opérationnel et leur test, sur 266 bassins versants.

• Une analyse conjointe de l’unité HYCAR de l’INRAE (alors IRSTEA) avec les SPC Loire-Cher-Indre et Seine-Marne-Yonne-Loing (Pérédo et al., 2018) du comportement du modèle GRP et de ses limites lors des crues citées plus haut de mai-juin 2016, avec le constat, notamment, de sous-estimation des volumes ruisselés, ainsi que pour les crues sur des bassins versants proches en janvier 2018 (avec moins de sous-estimation), a permis de confirmer l’intérêt des pistes d’amélioration de (Pinna, 2017).
• La poursuite de ce chantier, notamment par une thèse (Astagneau, 2022), qui a :
  • approfondi le diagnostic sur le même jeu de données, en
    • identifiant les évènements pour lesquels les erreurs de prévision étaient les plus fortes, principalement pour des pluies intenses et géographiquement contrastées, surtout en été ou en début d’automne, lorsque l’humidité initiale du sol est faible, souvent lors d’évènements se situant en dehors des plages de ceux qui avaient été utilisés pour le calage des paramètres,
    • analysant les flux internes aux modèles utilisés (GRP et ses variantes en test),
    • essayant d’identifier les effets négatifs éventuels des méthodes d’évaluation des performances et les interférences dues au processus d’assimilation de la valeur du dernier débit observé,
  • proposé à son tour des améliorations sans trop complexifier le modèle et le jeu des paramètres, en testant des alternatives à la structure des modèles de la famille GR (GR5H et GRP),
  • et dégagé des perspectives :
    • en adaptant la version (avec une structure plus adaptée) du modèle GRP et les modalités de calage des jeux de paramètres aux caractéristiques de l’évènement attendu et son contexte, en évoluant donc vers un dispositif multi-modèles GRP,
    • en cherchant à limiter la surface des bassins versants modélisés, pour limiter la complexité des processus à simuler, ce qui implique soit d’exploiter les données de stations hydrométriques intermédiaires, soit d’avoir recours à la régionalisation, qui, notamment, estime des débits en des points non jaugés du réseau hydrographique, en évoluant donc vers une organisation semi-distribuée,
    • en rapprochant les démarches menées en matière de modélisation pour la prévision des crues et pour l’anticipation des crues soudaines (Piotte, 2020) et (PICS, 2023), et celles conduites concernant les modèles géographiquement distribués.

Les modèles géographiquement distribués, en partie à base (ou d’inspiration) physique (MARINE, ATHYS, et ALTHAÏR)

Cette voie a fait, en France, l’objet d’investigations depuis les années 1990 (Moussa, 1993) pour prendre en compte l’hydrologie générale de bassins versants hétérogènes, comme dans les Cévennes.

Pour les applications actuelles en prévision des crues, notamment, on pourra se référer :

• aux articles MARINE (HU), ATHYS (HU) et La prévision des crues à l’aide du modèle ALTHAÏR sur les bassins cévenols ;
• et à la Fiche B.25 – Modèles hydrologiques distribués de la Catégorie:Incertitudes.

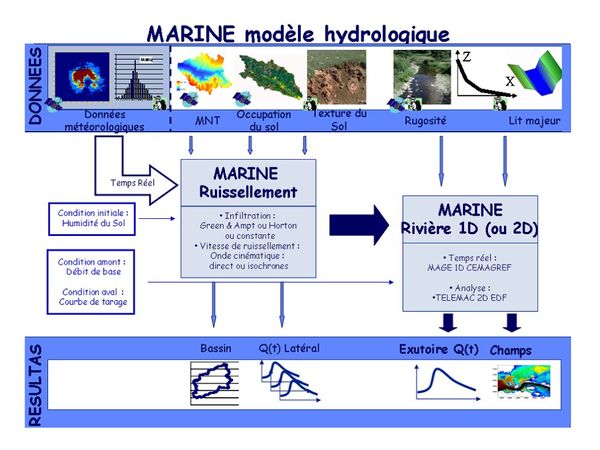
Ces modèles sont assez similaires. MARINE, développé par l’Institut de Mécanique des fluides de Toulouse (figure 6), ATHYS, conçu par HydroSciences de Montpellier et l’IRD, puis ALTHAÏR, développé et utilisé par le SPC GD, sont portés, pour la prévision des crues opérationnelle, sur la Plate-forme commune PLATHYNES (Narbaïs-Jaureguy et al., 2023). Ils sont adaptés pour des bassins versants dont les parties ont des caractéristiques assez contrastées et qui sont soumis à des crues rapides consécutives à des pluies consécutives intenses et inégalement réparties.

Figure 6 : Présentation synthétique de la structure du modèle MARINE ; Source :

D'autres modèles existent, comme :

• LARSIM, qui, lui, permet aussi de sectoriser par sous-bassins versants,
• MORDOR-TS (pour MOdèle à Réservoir, de Détermination Objective du Ruissellement, totalement Spatialisé), développé par EDF pour la prévision des crues et des étiages (En réalité il s'agit d'un modèle semi-distribué, le bassin versant étant découpé en sous bassins de superficie choisie, sachant, par ailleurs, que le modèle MORDOR-SD est, lui, découpé en bandes d’altitude) ; voir https://www.drias-eau.fr/accompagnement/sections/394.

Tous ces modèles reproduisent, en s’appuyant sur un maillage régulier et assez fin (1 km x 1 km est souvent conseillé car cette échelle kilométrique est un bon compromis entre la représentation du bassin, de son réseau de drainage, et ne génère pas des temps de calcul excessifs), les divers processus hydrologiques de production et de transfert, en s’appuyant sur des lois physiques ; par exemple, le modèle MARINE, au niveau de chaque maille et dans les échanges entre mailles, simule :

• l’interception et l’évapotranspiration ;
• l’infiltration dans le sol (modèle de Green et Ampt) ;
• les écoulements de subsurface (modèles de Darcy et Topmodel),
• les ruissellements de surface et dans le réseau hydrographique drainant le bassin versant (modèle de l’onde cinématique).

Pour les modèles de la plate-forme PLATHYNES, il est conseillé d’utiliser un maillage kilométrique, que l’on adapte pour obtenir un réseau hydrographique, certes dégradé, mais restant proche du réseau réel. C’est notamment indispensable pour positionner correctement dans les modèles l’exutoire et les stations de mesure.

Leurs données d’entrée concernant la pluie sont des images radar-météorologiques calibrées avec des mesures au sol, ou, sinon des interpolations des mesures ponctuelles au sol. Les variables d’état sont déduites de modèles numériques de terrain assez précis du bassin versant, de cartes d’occupation du sol et des caractéristiques pédologiques et géologiques, ainsi que de la description de la morphologie des cours d’eau drainant le bassin versant.

Ces modèles, développés à l’origine pour des bassins versants aux caractéristiques hétérogènes, sont aussi de plus en plus utilisés pour modéliser l’hydrologie de bassins versants moins hétérogènes, mais où les cours d’eau ne sont pas très densément instrumentés (ce qui est le cas général), en faisant un effort de régionalisation des paramètres des modèles simulant la relation « pluie sur chacune des mailles - débit à l’exutoire de ces mailles ». La régionalisation est une méthode générale consistant à extrapoler des informations acquises sur des bassins jaugés (disposant d’assez longues séries de mesures hydrométriques validées) à des bassins versants non jaugés. Appliquée à des modèles géographiquement distribués comme ceux de la plate-forme PLATHYNES, elle permet d’opérer une interpolation spatiale de la réponse hydrologique mesurée à l’aval d’un assez grand bassin versant (Voir en p. 279 du mémoire de thèse (Rouhier, 2018) portant sur la régionalisation du modèle MORDOR-TS). Cela ouvre des perspectives prometteuses pour étendre largement la prévision des crues à l’aval de nombreux sous-bassins versants.

Les procédures multi-modèles principalement hydrologiques

La plate-forme SOPHIE (HU) a permis, à partir de la deuxième moitié des années 1980, de fédérer dans une même plate-forme les diverses formules et les quelques modèles utilisés opérationnellement pour la prévision des crues, ce qui permettait de mettre en place un premier environnement commun pour la gestion des données d’entrée et des résultats, ainsi que pour comparer ces derniers, lorsque plusieurs modèles étaient mis en œuvre ; cet outil a constitué la ressource permettant d’attendre jusqu’en 2013 le début de la diffusion de la Plate-forme Opérationnelle de Modélisation (POM). La généralisation de l’utilisation de la POM dans les SPC et la mise en évidence des limitations des formules et modèles empiriques ont rendu caduc l’outil SOPHIE, dont les composants restant utiles ont été intégrés dans la POM.

Le principe du recours à des modélisations différentiées et à la comparaison de leurs résultats est une ressource précieuse pour consolider l’évaluation des incertitudes de prévision. La POM le rend possible. Ces multi-modèles peuvent être de la même famille (GRP, comme on l’a vu plus haut), mais aussi favorisent une complémentarité et un rapprochement des modèles conceptuels et des modèles distribués d’inspiration physique (sans que cela ne nécessite beaucoup plus de mesures, notamment en temps réel).

L’intérêt pour les procédures multi-modèles reste d’actualité, en hydrologie générale : on peut citer par exemple (Arsenault, 2015) et (Thébault, 2023).

Les modèles hydrauliques (ou hydrodynamiques) de prévision de la propagation des ondes de crue

Les fonctions et principales caractéristiques des modèles hydrauliques

La simulation de la propagation d’une onde de crue permet de prévoir les changements que subira l’hydrogramme qui la représente au cours de sa propagation dans le système hydraulique, le long des tronçons modélisés de cours d’eau, entre deux confluences majeures. Ces changements résultent :

• de la diffusion de l'onde de crue qui se traduit par un amortissement du pic de crue, un allongement de la durée de l'hydrogramme et un décalage temporel ;
• des apports intermédiaires ou des particularités rencontrées sur le parcours (stockage ou lâcher d’eau au niveau d’un barrage-réservoir, par exemple).

Et à ces confluences majeures, ces modèles composent les apports du cours d’eau principal et d’un ou plusieurs affluents.

Il existe deux grandes familles de modèles de propagation et de composition des crues :

• les modèles simplifiés, apparentés aux modèles analogiques numériques (dits parfois « hydrologiques ») et résultant de simplifications des équations Barré de Saint- Venant (Vérifier sa présence et son titre dans Wikhydro), par exemple : le modèle Muskingum (Voir Muskingum (modèle) (HU)), malgré ses défauts structurels, ou le modèle de l’onde cinématique, souvent empiriques ou conceptuels et globaux ; ils s'intéressent principalement aux transformations des hydrogrammes au cours de leur transfert dans le cours d’eau ; ou les modèles basés sur des hydrogrammes unitaires de type Hayami, ou plus récemment MOHYS ;
• les modèles hydrauliques ou hydrodynamiques reposent sur les équations de Barré de Saint-Venant (Barré de Saint-Venant (équations de ) (HU) ; ils représentent à la fois le débit et les grandeurs hydrauliques qui le caractérisent (hauteur et vitesse moyenne) ; ces modèles nécessitent des informations détaillées sur la géométrie et la rugosité des tronçons du cours d’eau, ainsi que des méthodes de calcul plus élaborées ; ce sont ceux qui sont aujourd'hui les plus largement utilisés ; ils peuvent être monodimensionnels (1D) ou bidimensionnels (2D).

Pour des questions de temps de calcul et de quantité de données à fournir, on adopte en priorité les modèles 1D dans les zones sans très forts enjeux, ou avec des lits majeurs assez étroits

Cette représentation peut être insuffisante dans les autres cas, pour lesquels on pourra utiliser pour simuler les écoulements en lit majeur :

• l’ajout à un modèle 1D utilisé sur le lit mineur, et éventuellement sur les principaux chenaux d’écoulement en lit moyen ou majeur, d’un modèle à casiers permettant de représenter les transferts d'eau, d'une part entre le lit mineur et les principaux chenaux d’écoulements, et d'autre part les zones d’expansion de crue dans les lits moyen et majeur ; ces modèles à casiers sont d'autant plus pertinents que les trois types de lits sont assez bien compartimentés par des infrastructures en remblais, des digues latérales ou des talus routiers ou ferroviaires, qui contraignent les écoulements en lit majeur et conditionnent les stockages consécutifs aux débordements ; les échanges entre casiers sont régis par des lois de transfert (souvent des lois de déversoirs ou d’orifices) ;
• des modèles à 2 dimensions (2D) horizontales, dans le cas où les écoulements vont, au sein du lit mineur (par exemple dans un estuaire large comme la Gironde) ou de la zone inondée, dans plusieurs directions horizontales ; ces modèles fournissent le niveau d’eau ainsi que les composantes horizontales de la vitesse en tous points d’un maillage reposant sur une grille de calcul horizontale ; ils nécessitent des données topographiques et bathymétriques suffisamment précises, en altimétrie (une à deux dizaines de centimètres) et en résolution horizontale (variant de quelques mètres à quelques dizaines de mètres, suivant que les variations altimétriques sont marquées ou pas) ; ils permettent aussi de représenter les écoulements de manière relativement concrète, sur des cartes dynamiques, ce qui facilite la communication au public. Mais ils sont plus lourds à mettre en œuvre, notamment pour la collecte des données nécessaires, même si de très notables progrès ont été faits depuis le début des années 2010 sur la disponibilité et la précision des informations topographiques. Ces modèles 2D peuvent aussi être très utiles pour simuler des écoulements localisés aux abords d’un ouvrage ou d’une autre singularité hydraulique ou consécutifs à l’ouverture d’une brèche dans une digue.

La spécificité des modèles hydrauliques pour la prévision des crues par rapport à ceux qui sont utilisés en simulation pour évaluer les risques ou les effets d’aménagements est moins forte que pour les modèles hydrologiques. Elle est centrée sur la capacité à :

• recevoir en données d’entrée : les résultats des modèles hydrologiques, les mesures hydrométriques en temps réel et des informations éventuelles sur des modifications du contexte hydraulique ;
• exécuter les calculs et fournir les résultats dans des délais obligatoirement assez courts.

Ces modèles peuvent donc résulter assez facilement d’adaptations de modèles ayant déjà été mis en place pour d’autres fonctions (élaborer des Plans de prévention des risques d’inondation, évaluer les options d’une stratégie de réduction de ces risques, …) ce qui s’est produit, par exemple dans le cadre de Plans grands fleuves ou des PAPI. Les contraintes opérationnelles nécessitent tout de même de privilégier des modèles à la fois robustes informatiquement (peu sujets à des interruptions ou des pannes) et d’exécution rapide, ce qui oblige parfois à simplifier ou reconfigurer ces modèles, voire à coupler de la modélisation 1D (grands corridors) et de la modélisation 2D (lits mineurs ou majeurs larges, zones de confluences, présence d’ouvrages hydraulique et d’enjeux forts et différenciés, …) comme le permettent les suites MASCARET-TELEMAC ou HEC-RAS.

Les divers modèles hydrauliques utilisés et ceux qui ont été choisis pour un soutien prioritaire

Les modèles hydrauliques utilisés pour la prévision des crues

Les modèles hydrauliques, ou hydrodynamiques, actuellement utilisés dans le réseau pour la prévision des crues en France sont présentés dans les paragraphes suivants.

MOHYS

Il s'agit d'un modèle de propagation simplifié, rapide et souvent performant, qui s'apparente à un modèle de type Lag&Route en :

• propageant un hydrogramme amont selon un temps de propagation qui peut être ajusté en fonction d'un indicateur (une classe de niveau d’eau ou de débit),
• réalisant ensuite une amplification par application d'un coefficient (ratios de surfaces de bassins versants) pour prendre en compte les apports intermédiaires entre le bassin drainé à une station en amont et le bassin jusqu'à la confluence avec le cours d’eau principal,
• représentant le laminage, ou l’amortissement de l’onde de crue au cours de sa propagation et par débordements,
• lissant le signal via un hydrogramme unitaire, ce qui est notamment nécessaire si la station amont est une sortie de barrage.

MOHYS est le modèle le plus utilisé actuellement par certains SPC. Il est intégré dans la plate-forme PLATHYNES depuis 2023.

MASCARET

MASCARET (Open TELEMAC-MASCARET, 2023) et (Le Pape et al., 2024), a été développé notamment par le Laboratoire National d’Hydraulique – LNH – de la R&D d'EDF avec le CEREMA (ex-CETMEF) et le bureau d’études ARTELIA, ainsi que d’autres organismes français, européens et internationaux. Il fait partie de la suite MASCARET - TELEMAC, qui est un ensemble de codes de calculs scientifiques couplés et parallélisés, dédiés à la modélisation de l’hydraulique environnementale à surface libre, qui regroupe des codes 1D, 2D et 3D, permettant de modéliser et prédire tous les écoulements liés à l’eau : cours d’eau, réservoirs et lacs, mers et océans, divers transports solides, qualité de l’eau, etc.

MASCARET est un modèle hydrodynamique 1D (monodimensionnel suivant l’axe longitudinal du cours d’eau à surface libre découlant des équations de Saint-Venant avec reconstruction non-hydrostatique, formulées suivant la méthode des éléments finis. Il permet des calculs en régimes : fluvial et trans-critique permanent ; fluvial non permanent ; et trans-critique non permanent. Le code prend en charge des profils complexes incluant un grand nombre de points descriptifs. Outre le lit mineur des cours d’eau, il peut prendre en charge des profils complexes pour intégrer plus précisément les parties de l’écoulement dans les lits majeurs contributifs (cas de vallées assez étroites ou de chenaux dans les vallées plus larges), dont les mises en eaux puis hors d’eau peuvent se faire de manière progressive. Le code prend en charge des profils complexes incluant un grand nombre de points descriptifs.

Il inclut aussi un module CASIER, à casiers interconnectés pour prendre en compte principalement les stockages temporaires dans les zones inondables.

On peut aussi coupler MASCARET avec TELEMAC-2D, grâce à une interface homme-machine commune et un processus d’interconnexion. Cette suite est composée de logiciels libres, gratuits et bénéficie d’une communauté d’utilisateurs et développeurs. Depuis 2015, le bureau d’études Artelia gère la maintenance du code Mascaret dans le cadre du Consortium TELEMAC-MASCARET et intègre les développements des contributeurs.

Figure 7 : : Positionnement des profils en travers (en rouge) pour la modélisation hydraulique avec MASCARET des écoulements dans les lits mineur et majeur de l’Adour et des Gaves réunis au niveau et à l’aval de leur confluence ; Source : Open TELEMAC-MASCARET

Une première interface (Fudaa) entre l’utilisateur et Mascaret aidait à construire une base du modèle, non géoréférencée, comprenant déjà la construction de casiers. Une nouvelle interface de construction et d’étude a été développée, d’abord par le SPC Maine Loire aval (DREAL Pays de la Loire) sous forme d’un prototype de plugin QGIS, qui a ensuite été régulièrement améliorée sous pilotage du SCHAPI, en association avec le CEREMA, qui a notamment enrichi les fonctionnalités liées aux casiers et contribué à l’organisation des retours de la part des utilisateurs. Le plugin de QGIS est diffusé par ARTELIA, et bénéficie d’une documentation en ligne (https://github.com/Artelia/Mascaret/wiki).

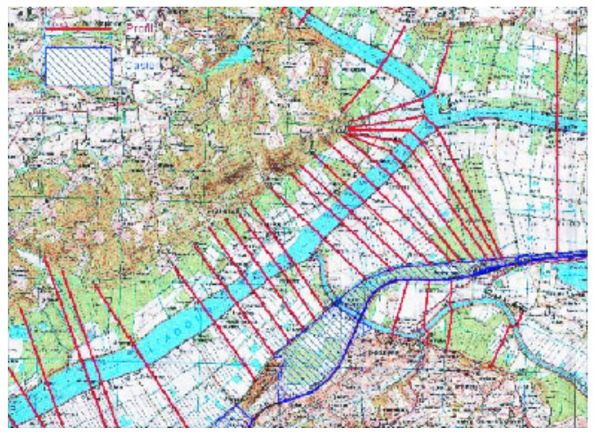
Le tracé des profils en travers est effectué à la main par des lignes brisées (Voir Figure 6), autant que possible perpendiculaires à l’axe principal d’écoulement. Le plugin Mascaret permet ensuite d’extraire la topographie à partir d’une dalle de Modèle Numérique de Terrain (MNT) préalablement chargée dans QGIS puis de compléter avec des profils topo-bathymétriques relevés sur le terrain et éventuellement des valeurs altimétriques de points situés sur ces profils en travers, interpolées entre celles disponibles pour des points alentour. Le modélisateur définit ensuite les limites du lit mineur, du lit majeur et éventuellement des zones de stockage (ne participant guère à l’écoulement). Il prend ensuite en compte les transformations des écoulements par les singularités hydrauliques ponctuelles, en 1D (pont, dalot, seuil - éventuellement mobile -, orifice, …) en définissant des sections de calcul où les équations de Saint Venant sont remplacées, en respectant la conservation des débits entre amont et aval, par une loi « d’ouvrage » adaptée à la nature de cette singularité, et choisie dans un catalogue complet d’abaques, dont les paramètres découlent de la description des caractéristiques géométriques de l’« ouvrage » à décrire avec une interface graphique spécifique.

Le réseau hydrographique doit ensuite être défini grâce à des « branches » interconnectées au niveau des confluences ou des diffluences. Les branches constituent la colonne vertébrale d’un modèle, en reliant tous les objets qui le constituent (profils en travers et singularités, apports, pertes, ...) ; ce référencement linéaire permet de passer du référentiel géographique (celui du SIG, à partir de données géoréférencées) et de la construction graphique des singularités, au référentiel du modèle hydraulique 1D. Les branches sont délimitées par les « extrémités » sur lesquelles on applique différents types de conditions aux limites (débits, niveaux d’eau, courbes de tarage, …).

Il est également possible de définir des casiers interconnectés aux branches et entre eux grâce à : des lois paramétrables ; des ouvrages paramétrables (comme vu plus haut, pour les « ouvrages » sur les cours d’eau modélisés) ; ou des apports ou prélèvements ponctuels ou sur un linéaire.

Cette interface SIG est une véritable avancée pour la construction et la diffusion (et l’appropriation) des modèles « Mascaret ». Le plugin permet au modélisateur de saisir les données à utiliser par le code Mascaret de manière plus rapide et plus fiable, sous contrôle par visualisation cartographique, de même que l’ergonomie d’ensemble rend plus facile et plus sûre la construction de modèles sur de grandes emprises, de plusieurs dizaines de kilomètres et plusieurs centaines de profils en travers, avec des singularités. L’interface utilisateur antérieur Fudaa ne permettait ce travail qu’au prix de fastidieuses manipulations de données sur tableur, ce qui freinait le déploiement des modèles Mascaret, notamment dans le réseau Vigicrues.

Figure 8 : : Exemple de visualisation d’un modèle géoréférencé dans le Plugin QGis Mascaret, concernant la Loire aval de Chalonne à l’Océan ; Source : Le Pape et al. (2024).

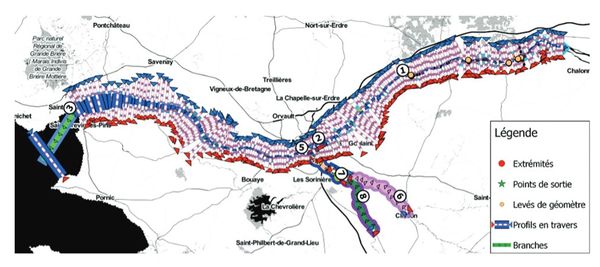
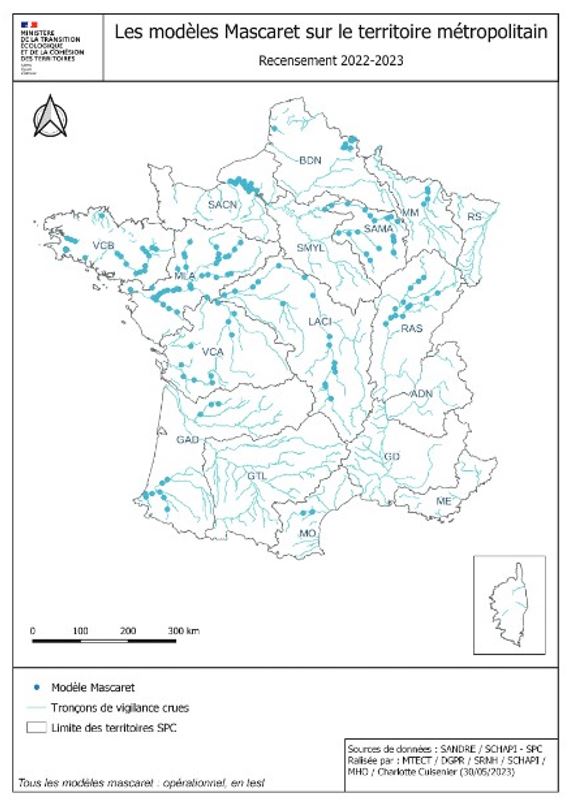
Dès 2006, un modèle Mascaret a été construit sur un secteur influencé par la marée : l’Adour aval, un des cas où il devenait impératif de disposer d’un modèle permettant de prendre en compte cette influence aval (maritime, en l’occurence) aussi bien que celle des crues générées en amont. Petit à petit d’autres modèles MASCARET de prévision des crues ont été construits pour : la Laïta, la Seine aval, la Loire aval, la Marne, l’Aube, etc. A partir de 2017, la construction de modèles Mascaret a plus rapidement augmenté : d’une petite dizaine alors, à une cinquantaine en 2023 ; la plupart des 17 SPC étaient dès lors dotés d’au moins un modèle MASCARET (Voir Figure 9) ; et pour certains des SPC tous les tronçons de cours d’eau où la propagation des crues est dominante pour la prévision en sont couverts. Cette montée en puissance a été accompagnée par des formations spécifiques pour une cinquantaine de modélisateurs, ainsi que de développements en interne dans plusieurs SPC et par le CEREMA. La construction de modèles MASCARET a vocation à se poursuivre notamment sur les zones à forts enjeux surveillés par Vigicrues.

Figure 9 : Recensement en 2022 et 2023 des modèles MASCARET utilisés pour la prévision des crues en France sur le territoire métropolitain ; Source : Le Pape et al. (2024).

TELEMAC-2D

Le logiciel TELEMAC-2D (Open TELEMAC-MASCARET, 2023) et (TELEMAC-2D Manuel de l’utilisateur, 2010) résout les équations de Barré de Saint-Venant à deux dimensions horizontales. Ses résultats principaux sont, en chaque point du maillage de résolution, la hauteur d’eau et la vitesse moyenne sur la verticale. TELEMAC-2D trouve ses applications en hydraulique à surface libre, maritime ou fluviale. Il est capable de prendre en compte une multitude de phénomènes physiques, notamment, dans notre domaine : le frottement sur le fond ; l’influence de la force de Coriolis ; l’influence de phénomènes météorologiques (pression atmosphérique et vent) ; la turbulence ; les écoulements torrentiels et fluviaux ; les zones sèches dans le domaine de calcul (bancs découvrant et plaines inondables) ; le traitement de singularités (seuils, digues, buses, etc.) ; le couplage avec le transport sédimentaire ; etc.