Modèle d'écoulement en réseau et en cours d'eau (HU)

Traduction anglaise : Flood routing models for pipes and channels

Dernière mise à jour : 11/06/2024

Mot en chantier

Modèle mathématique permettant de représenter la propagation et la transformation d'une onde de crue dans un système hydraulique (réseau d'assainissement ou réseau hydrographique de surface) et/ou de calculer les hauteurs d'eau atteintes et de déterminer les zones potentiellement inondées.

Fonctions des modèles d'écoulement

Les modèles d'écoulement font généralement suite à des modèles hydrologiques et s'intègrent dans une représentation dite semi-distribuée (ou détaillée) du système hydrologique simulé (figure 1). Les modèles hydrologiques produisent des hydrogrammes aux exutoires des bassins versants et ces hydrogrammes sont ensuite introduits puis propagés dans les tronçons du réseau hydrographique, naturel ou artificiel, combinés aux jonctions, et transformés au passage d’ouvrages spéciaux par les modèles d'écoulement. Les modèles d'écoulement nécessitent donc une représentation adaptée de ce réseau hydrographique.

Figure 1 : Les modèles construits pour représenter le fonctionnement des grands réseaux d'assainissement par temps de pluie peuvent utiliser des centaines de sous-bassins versants et des milliers de tronçons ; ici le bassin versant à l'amont de la station d'épuration de Saint-Fons, Communauté urbaine de Lyon (les sous-bassins versants en grisé et les tronçons de réseau en traits gras) ; Source : logiciel Canoe.

Les modèles d'écoulement doivent donc remplir différentes fonctions :

• représenter le décalage temporel et l'amortissement de l'hydrogramme de crue lors de son transfert dans un tronçon ;
• représenter la composition des hydrogrammes aux jonctions, et leur séparation éventuelle aux défluences ;
• représenter l'impact des différents ouvrages (en particulier de stockage : seuil, barrage, bassin de retenue, etc.) et singularités hydrauliques (seuils, chutes, influences aval, etc.), ainsi que celui des débordements dans les zones inondées, sur la façon dont l'hydrogramme est transféré.

Ces fonctions obligatoires sont complétées par des fonctions supplémentaires qui peuvent être remplies par le modèle lui-même ou par un post-traitement (voir le § suivant) :

• représenter les grandeurs hydrauliques (hauteur et vitesse) associées aux valeurs de débit ;
• en déduire les hauteurs d'eau atteintes dans le lit majeur et l'extension éventuelle de la zone inondée.

Modèles hydrauliques et modèles de transfert d'onde

Il existe trois grandes familles de modèles :

• les modèles issus de la Mécanique des fluides qui résolvent numériquement les équations de Navier-Stokes à 2, 3 ou 4 dimensions ;
• les modèles utilisant les équations de Barré de Saint Venant à 1 ou 2 dimensions ;
• les modèles conceptuels de transfert d'onde.

Modèles issus de la MFN

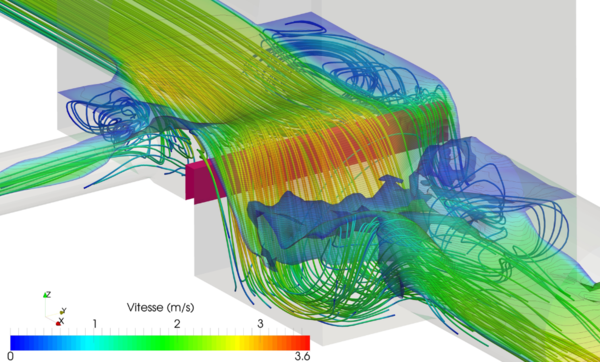
Les modèles de mécanique des fluides numérique sont aujourd'hui des outils extrêmement puissants, capables de représenter les écoulements à surface libre, en régime permanent ou transitoire, avec 1, 2 ou 3 dimensions d'espace (figure 2). On parle également de CFD pour Computational Fluid Dynamics ou de modélisation 3D (même si parfois on n'utilise pas les trois dimensions d'espace).

Ces modèles sont cependant extrêmement gourmands en temps calcul et en place mémoire et ne sont encore utilisés que pour des applications limitées ne concernant qu'un petit linéaire et/ou une singularité hydraulique. Ils sont cités ici pour mémoire car il est possible que dans quelques années les progrès de l'informatique permettent de les utiliser de façon plus opérationnelle pour représenter des systèmes hydrauliques complets.

Figure 2 : Évolution de la surface libre dans un déversoir frontal calculée avec un outil de Mécanique des fluides numérique ; Crédit José Vazquez.

Pour en savoir plus, voir l'article Mécanique des fluides numérique / MFN (HU).

Modèles utilisant les équations de Barré de Saint Venant

Les équations de Barré de Saint Venant permettent de représenter les écoulements à surface libre non permanents, unidimensionnels ou bidimensionnels. Suivant la manière dont elles sont écrites et la manière dont elles sont résolues, il est possible de calculer les écoulements graduellement variés avec ou non prise en compte du ressaut hydraulique et d’un front d’onde correspondant à des variations rapides du débit (Marc BUYER 2002).

L’écriture classique des équations de Barré de Saint-Venant repose sur deux deux hypothèses fortes :

• l'écoulement doit être graduellement varié ;
• la répartition des pressions doit être hydrostatique.

Ces équations peuvent également être adaptées, et c'est important dans le cas des réseaux d'assainissement, pour représenter les écoulements en charge (voir Fente de Preismann (HU)).

Même si ces hypothèses ne sont pas toujours vérifiées, en particulier dans le cas des crues rapides, l'expérience montre que ce modèle permet de représenter la propagation des crues de façon très satisfaisante, que ce soit en rivière ou en réseau d'assainissement. De plus, comme il utilise la vitesse et la section mouillée (ou la hauteur d'eau) comme variables principales de calcul il est également capable de calculer les lignes d'eau, et, dans le cas des équations bidimensionnelles, de déterminer directement les zones inondées.

Formulation classique

Le plus souvent les équations de Barré de Saint Venant s'écrivent sous la forme synthétique suivante :

à une dimension (modèle dit 1D ou filaire) :

$ \frac{\partial U}{\partial t}+\frac{\partial F(U)}{\partial x}=S(U) \quad(1) $

et, à deux dimensions (modèle dit 2D ou multidirectionnel) :

$ \frac{\partial U}{\partial t}+\frac{\partial F(U)}{\partial x}+\frac{\partial F(U)}{\partial y}=S(U) \quad(2) $

Nota : Les expressions "modèle 1D" ou "modèle 2D" sont parfois mal comprises, certains les interprétant comme "dans 1 ou 2 directions privilégiées" ; c'est pourquoi il vaut sans doute mieux parler de "modèle filaire" et de "modèle multidirectionnel".

Dans les deux cas :

• $ U = \displaystyle\binom{S}{V} \quad(3) $ représente le vecteur des variables conservatives (vitesse moyenne et section mouillée) ;
• $ F(U) = \displaystyle\binom{Q}{\frac{V^2}{2} + g.h}\quad(4) $ représente les flux (débit et énergie) ;
• $ S(U) = \displaystyle\binom{q}{g.(I-J)} \quad(5) $ représente les termes sources (débit entrant et apport ou perte d'énergie) ;

Avec :

• $ h $ : Hauteur d'eau (m) ;
• $ S $ : Section mouillée (m²) ;
• $ V $ : Vitesse moyenne dans la section droite (m/s) ;
• $ Q $ : Débit (m³/s) ( $ Q = V.S $) ;
• $ g $ : Accélération de la pesanteur (m/s²) ;
• $ q $ : Apport ou perte latérale de débit (m³/s) ;
• $ I $ : Pente du fond (m/m) ;
• $ J $ : Pertes de charge par unité de longueur (pente de la ligne d'énergie) (m/m).

Simplification des équations

Les différents termes apparaissant dans la deuxième équation de Barré de Saint Venant peuvent prendre des valeurs très variées.

Il arrive donc souvent que certains soient négligeables par rapport aux autres. Il est alors possible de simplifier cette équation et de construire des modèles plus faciles à intégrer. La simplification la plus courante consiste à considérer les termes d'inertie et d'accélération convective comme négligeables. On obtient alors le modèle de l'onde de crue diffusante :

$ g.\frac{\partial h}{\partial x}=g.(I-J)\qquad(6) $

Mais, même s'ils donnent des résultats souvent acceptables dans de nombreux cas, ces modèles simplifiés ont perdu beaucoup d'intérêt avec le développement d'ordinateurs et de logiciels qui permettent de résoudre rapidement les équations complètes, y compris sur des réseaux complexes.

Formulation conservative

Il est possible de modifier la formulation classique précédente (relations 1 à 5), pour obtenir une formulation dite conservative permettant de prendre en compte les ressauts hydrauliques et les fronts d’onde (Toro, 2009). A une dimension, cette formulation est constituée des deux équations suivantes :

$ \frac{\partial S}{\partial t}+\frac{\partial Q}{\partial x}=q \qquad(7) $

$ \frac{\partial Q}{\partial t}+\frac{\partial {(\frac{Q^2}{S}+g.I_1)}}{\partial x}=g.S.(I-J) \qquad(8) $

en posant :

$ I_1 = \int_0^h{(h-η)}.B.dη\qquad(9) $

Avec :

• $ B $ : largeur miroir (m).

Pour prendre en compte les ressauts hydrauliques et les fronts d'onde, il est nécessaire de résoudre ce système d'équations en utilisant un schéma numérique à capture de choc (Toro, 2009).

Pour en savoir plus, voir l'article Barré de Saint Venant (équations de) (HU).

Modèles conceptuels de transfert d'onde

Les modèles de propagation d'onde de crue sont des modèles conceptuels permettant de simuler la propagation des ondes de crue dans un système hydrologique.

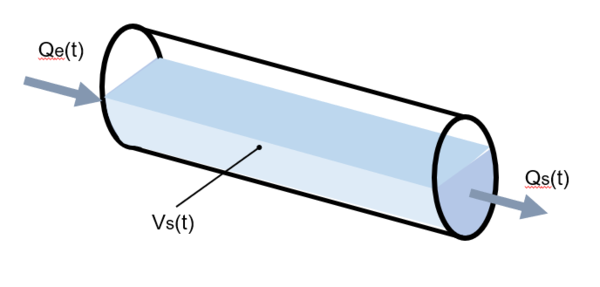
Ces modèles reposent sur l'équation de continuité (relation 10) à laquelle on associe généralement une équation de stockage reliant le volume stocké dans le tronçon aux débits observés ou simulés aux extrémités amont (débit entrant) et/ou aval (débit sortant) du tronçon (relation 11 et figure 3) :

$ Q_s(t) = Q_e(t)- \frac{dV_s(t)}{dt}\qquad(10) $

$ V_s(t) = f(t, Q_e(t), Q_s(t))\qquad(11) $

Avec :

• $ Q_e(t) $ : débit à l'entrée du tronçon (m³/s) ;
• $ Q_s(t) $ : débit à la sortie du tronçon (m³/s) ;
• $ V_s(t) $ : volume stocké dans le tronçon (m³).

Figure 3 : Dans les modèles de propagation d'onde de crue, la deuxième équation est le plus souvent obtenue en reliant le volume stocké dans le tronçon aux débits amont et aval par une expression simple, souvent linéaire.

Les modèles de transfert d'onde les plus connus sont le modèle Muskingum, le modèle de translation simple et le modèle de stock. Dans certains cas, il est même possible d'établir un lien entre ces modèles conceptuels et les modèles simplifiés issus des équations de Barré de Saint Venant (Cunge, 1969).

Pour en savoir plus, voir l'article Modèle de propagation d’ondes de crue (HU).

Représentation du réseau hydrographique

Les modèles d'écoulement en réseau et en cours d'eau, qu'ils s'agissent de modèles hydrauliques (comme les équations de Barré de Saint Venant) ou de simples modèles de transfert d'ondes de crue (comme le modèle Muskingum), nécessitent de décomposer le réseau hydrographique étudié en éléments simples sur lesquels il sera possible d'appliquer les équations adéquates. Ces éléments sont de plusieurs natures :

• des nœuds (qui limitent et connectent les autres objets et permettent de relier les sous-bassins versants au réseau), définis par leurs coordonnées et leur altitude ;
• des ouvrages spéciaux ou des singularités, qui peuvent être considérés comme ponctuels, par exemple une chute ou un seuil, et qui sont alors affectées à un nœud, ou qui peuvent avoir une certaine extension spatiale (lac naturel ou retenue de barrage, bassin de retenue, etc.) (voir § "Importance des singularités hydrauliques et ouvrages spéciaux") ; chaque famille réclame une description spécifique ;
• des tronçons de cours d'eau ou de réseau, supposés homogènes qui discrétisent le réseau hydrographique ; un tronçon est défini par ses extrémités, sa longueur, sa pente, son profil en travers (ou les profils en travers à ses deux extrémités), sa rugosité (ou ses rugosités si on distingue plusieurs lits).

Nota : Historiquement, on disait souvent "bief" à la place de tronçon, en référence au vocabulaire de la navigation, et ce terme est encore parfois utilisé.

Principes du découpage en tronçons

Le découpage en tronçons est généralement effectué en essayant de conserver des portions aussi homogènes que possible (en profils en travers, pente, nature de matériaux, rugosité, etc.) du système à représenter.

• Dans le cas de la modélisation hydraulique des systèmes d’assainissement, les tronçons sont généralement considérés comme homogènes en pente, rugosité et forme de section.
• Dans le cas de la modélisation d'un cours d'eau, on raisonne plutôt à partir de points particuliers où les caractéristiques du bief sont connues et on considère que la rugosité et la forme de la section évoluent progressivement par interpolation linéaire entre celles des deux sections caractéristiques qui le limitent. En revanche on fait toujours l'hypothèse de la constance des autres paramètres tout le long du tronçon de calcul.

Importance des singularités hydrauliques et ouvrages spéciaux

Les systèmes hydrographiques, qu'ils soient naturels ou artificiels, contiennent souvent de nombreuses singularités hydrauliques et ouvrages spéciaux qui vont jouer un rôle important (et même souvent principal dans le cas des systèmes d'assainissement) sur le transfert de l'onde de crue. Ils doivent donc être correctement décrits et représentés par des modèles hydrauliques adaptés. L'expérience montre que c'est le plus souvent la difficulté à bien représenter ces éléments qui limite les performances des modèles d'écoulement. On trouvera, en particulier mais pas seulement, pour l’hydrologie urbaine, une présentation des modèles utilisables aux articles : Déversoir d'orage (HU) (et autres articles associés), Seuil hydraulique (HU), Chute (HU), Vanne (HU), Orifice (HU), etc.

Dans le cas de l'utilisation des équations de Barré de Saint Venant, ces singularités jouent un rôle particulièrement important sur les valeurs calculées de vitesse et de hauteur. En effet les hypothèses prises en compte pour les équations ne sont plus valides. Ceci pose des difficultés multiples, par exemple :

• dans un réseau d'assainissement, pour calculer le débit rejeté par un déversoir d'orage ;
• dans le cas de la prévision des crues de cours d'eau, pour comparer la hauteur d'eau calculée par le modèle et celle mesurée sur le terrain, les stations de mesure étant souvent placée à proximité d'un pont.

Représentation des zones susceptibles d'être inondées

Les zones susceptibles d'être inondées peuvent être intégrées dans la description des tronçons. Dans ce cas le profil en travers va distinguer a minima un lit mineur et un lit majeur. Elles peuvent également être représentées par des objets spécifiques. La situation est différente selon que l'on travaille sur un réseau d'assainissement ou sur un réseau hydrographique naturel.

Cas des réseaux d’assainissement

Dans le cas des réseaux d'assainissement les zones affectées par les débordements sont situées en surface. Elles sont donc totalement différenciées du réseau souterrain lui-même. Deux modes de représentation différents peuvent être utilisées selon la modélisation envisagée pour déterminer les zones inondées (voir § "Détermination des hauteurs d'eau et des zones inondées") :

• représenter simplement un réseau de surface (essentiellement composés par les rues) constitué de tronçons de canaux (eux-mêmes décrits de la même façon que précédemment par leur profil en travers, pente, nature de matériaux, rugosité, etc.), communiquant entre eux et communiquant avec le réseau souterrain ;
• utiliser un MNT pour représenter la surface de la ville ; ce second mode étant principalement utile lorsque les volumes épanchés en surface deviennent extrêmement importants.

Il peut également être nécessaire de représenter d'autres réseaux souterrains (par exemple le réseau de métro) ainsi que les relations avec le réseau hydrographique de surface (Paquier, 2009).

Cas des cours d'eau

La représentation différenciée des zones d'épanchement des crue est principalement faite lorsque l'on utilise des modèles à casier (voir § suivant). Dans ce cas il faut décrire chacune des zones susceptibles d'être inondée par une surface, une altitude moyenne et les liens qu'elle entretient avec le lit mineur du cours d'eau, ou les chenaux d’écoulement en lit moyen, et les zones adjacentes, en particulier suivant la nature des connexions (seuil, orifice, etc.). On peut aussi avoir recours à un modèle multidirectionnel couplé avec le modèle filaire représentant des écoulements principaux.

Détermination des hauteurs d'eau et des zones inondées

Connaître l'évolution des débits à chacun des points d'intérêt n'est pas suffisant. Il faut aussi connaître les hauteurs d'eau atteintes, condition indispensable pour prévoir les débordements de réseaux d'assainissement ou les zones susceptibles d'être inondées par les crues des cours d'eau. Cette détermination est difficile car la relation entre le débit et la hauteur d'eau n'est absolument pas univoque (à titre d'exemple, dans le cas d'une crue fluviale, le maximum de hauteur d'eau peut se produire plusieurs jours après le pic de débit).

Limites des approches utilisant des modèles de transfert d'onde

Dans le cas de l'utilisation d'un modèle de propagation d'onde de crue, le seul résultat connu est la valeur des débits. Il est donc nécessaire d'utiliser un post-traitement pour en déduire les valeurs de hauteurs d'eau. Du fait de la remarque précédente sur la non univocité de la relation entre hauteur et débit pendant les périodes de crue, il n'est généralement pas suffisant de rechercher la section mouillée et la hauteur avec une simple hypothèse de régime uniforme. Il est bien sûr possible d'améliorer la prévision en calculant, a posteriori, une ligne d'eau en régime graduellement varié à partir des valeurs maximum de débit, mais la validité des hauteurs d'eau atteinte restera faible.

Le calcul des zones inondées, nécessite donc, au moins dans les zones à enjeux, d'utiliser des modèles hydrauliques fournissant à la fois les valeurs de hauteurs et de débit.

Cas des réseaux d'assainissement

Dans le cas des réseaux d'assainissement les écoulements se font essentiellement (du moins en France) dans des sections fermées et enterrées. Pour que l'eau arrive en surface la conduite doit donc d'abord se mettre en charge et le débordement se produira lorsque la charge hydraulique deviendra supérieure à la profondeur de la conduite (voir Débordement (HU)).

En théorie, le calcul est donc simple car, si la conduite est en charge et que l'on néglige sa déformabilité ainsi que la compressibilité de l'eau, la relation entre le débit et la vitesse devient bijective, la section mouillée de l'écoulement restant constante puisque la conduite est pleine. Comme on sait établir une relation simple entre les pertes de charge et la vitesse et généraliser les équations de Barré de Saint Venant 1D au cas des écoulements en charge (voir Fente de Preismann (HU)), il suffit donc de tracer la ligne de charge pour trouver les endroits où elle dépasse le niveau du sol (figure 4), ce qui permet d'identifier les zones inondées. Cette méthode, disponible sur tous les outils actuels de simulation de réseau, fournit une première image déjà représentative.

Figure 4 : Débordement d'un réseau d'assainissement.

La réalité est cependant beaucoup plus compliquée pour deux raisons principales.

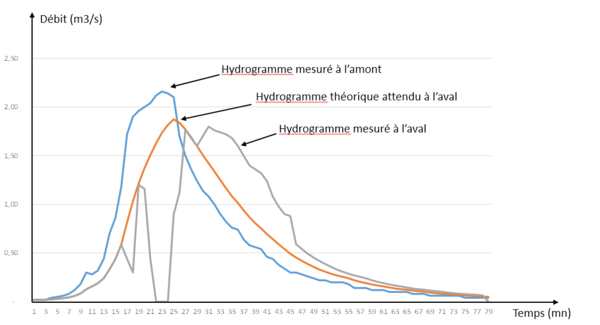
• Tant que l'eau s'écoule à surface libre dans la conduite, il y a de l'air au-dessus de la ligne d'eau ; au fur et à mesure que le niveau monte, cet air est comprimé et doit s'échapper ; le remplissage total de la conduite, surtout s'il est rapide, va donc s'accompagner de déplacements très brutaux de l'air piégé dans la partie haute et ces déplacements vont très fortement perturber l'écoulement de l'eau, donc la forme de l'hydrogramme (voir figure 5 et article Mise en charge (HU)) ; il n'existe actuellement pas d'outils opérationnel capable de prendre correctement ces phénomènes en compte.

Figure 5 : Exemple des perturbations produites par une mise en charge importante du réseau ; l'hydrogramme réel à l'aval de la zone perturbée est probablement encore plus chaotique que celui tracé ici qui est lissé du fait du pas de temps de stockage des mesures (dans ce cas 1 minute).

• L'eau arrivant en surface ne va généralement pas rester sur place, mais s'écouler dans le réseau de surface constitué par les rues et autres espaces urbains ; la détermination des zones réellement inondées impose donc de représenter aussi les écoulements dans ce réseau de surface. Deux solutions sont possibles :
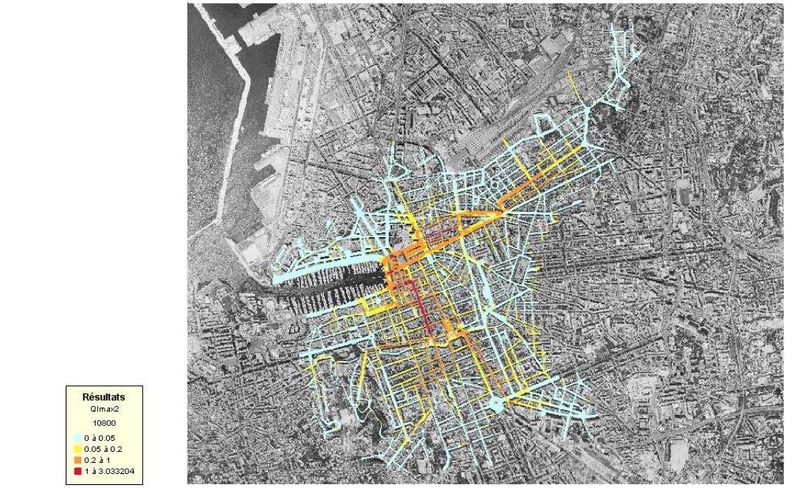
  • représenter simplement un réseau de surface (essentiellement composés par les rues) constitué de tronçons de "canaux" communiquant entre eux et communiquant avec le réseau souterrain et le représenter par un modèle hydraulique 1D (figure 6) ;
  • utiliser un MNT pour représenter la surface de la ville et utiliser un modèle multidirectionnel (2D) ; ce second mode étant principalement utile lorsque les volumes épanchés en surface deviennent importants.

Dans les deux cas il faut également représenter les connexions (dans les deux sens) entre le réseau souterrain et le réseau de surface par des ouvrages spéciaux adaptés (lois de seuil ou d'orifice).

Figure 6 : Exemple de représentation des zones urbaines inondées : débits unitaires maximaux sur le bassin versant du Vieux-Port à Marseille en cas de débordement du réseau d'assainissement ; Source : Paquier (2009).

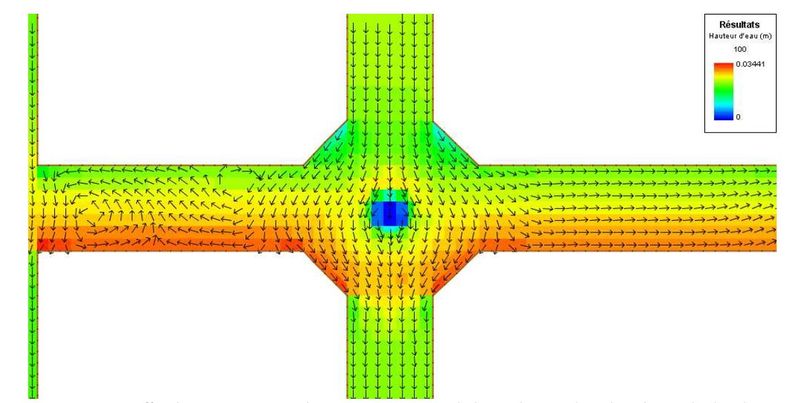
Dans les deux cas la modélisation des écoulements en surface reste cependant très difficile du fait de la grande complexité des interactions et de la variété et de la diversité des obstacles. A titre d'exemple la figure 7 montre l'effet d'un simple giratoire sur la répartition des hauteurs et des vitesses à un carrefour.

Figure 7 : Effet d’un giratoire sur les caractéristiques de l’écoulement (résultat d'un calcul 2D) ; Source : Paquier (2009).

Cas des cours d'eau

Dans le cas des cours d'eau, l'écoulement se fait toujours à surface libre et la difficulté consiste à bien représenter la façon dont l'eau peut sortir de son lit mineur ou des chenaux d’écoulements en lit moyen, généralement bien identifiables, pour aller occuper les différents espaces de son lit majeur, souvent protégés par des digues ou autres obstacles.

Deux approches sont possibles :

• l’ajout au modèle filaire (1D) utilisé sur le lit mineur, et éventuellement sur les principaux chenaux d’écoulement en lit moyen ou majeur, d’un modèle à casiers permettant de représenter les transferts d'eau, d'une part entre le lit mineur et les principaux chenaux d’écoulements, et d'autre part les zones d’expansion de crue dans les lits moyen et majeur ; ces modèles à casiers sont d'autant plus pertinents que les trois types de lits sont assez bien compartimentés par des infrastructures en remblais, des digues latérales ou des talus routiers ou ferroviaires, qui contraignent les écoulements en lit majeur et conditionnent les stockages consécutifs aux débordements ; les échanges entre casiers sont régis par des lois de transfert (souvent des lois de seuils ou d’orifices) ;
• l'utilisation d'un modèle hydraulique multidirectionnel (2D), dans le cas où les écoulements vont, au sein du lit mineur (par exemple dans un estuaire large comme la Gironde) ou de la zone inondée, dans plusieurs directions horizontales ; ces modèles fournissent le niveau d’eau ainsi que les composantes horizontales de la vitesse en tous points d’un maillage reposant sur une grille de calcul horizontale ; ils nécessitent des données topographiques et bathymétriques suffisamment précises, en altimétrie (une à deux dizaines de centimètres) et en résolution horizontale (variant de quelques mètres à quelques dizaines de mètres, suivant que les variations altimétriques sont marquées ou pas) ; ils permettent aussi de représenter les écoulements de manière relativement concrète, sur des cartes dynamiques, ce qui facilite la communication au public. Mais ils sont plus lourds à mettre en œuvre, notamment pour la collecte des données nécessaires, même si de très notables progrès ont été faits depuis le début des années 2010 sur la disponibilité et la précision des informations topographiques. Ces modèles 2D peuvent aussi être très utiles pour simuler des écoulements localisés aux abords d’un ouvrage ou d’une autre singularité hydraulique ou consécutifs à l’ouverture d’une brèche dans une digue. Ils peuvent tenir compte d'autres variables climatiques (par exemple le vent).

Lorsque l'on arrive dans une zone urbaine, les difficultés redeviennent les mêmes que dans le cas des réseaux d'assainissement. Par exemple, ces réseaux communiquent avec le cours d'eau et vont parfois fonctionner à contre sens en permettant à l'eau du cours d'eau de pénétrer dans les zones urbaines malgré la présence des digues (ce qui conduit parfois à installer des clapets anti-retour sur les exutoires des réseaux d'assainissement) (figure 8).

Figure 8 : Effondrement d'un collecteur d'assainissement, conséquence la crue de la Seine en 1910 ; Source : collection cartes postales Antonio Pelicer.

Bibliographie

• Cunge, J.A. (1969) : Au sujet d'une méthode de propagation de crue ; Journal of Hydraulics Research ; n°7 ; 1969 ; pp 205-230.
• Paquier, A. (2009) : Rapport final du projet RIVES "Risque d’inondation en ville et évaluation de scénarios" ; Synthèse ; irstea ; 2009, pp.13 ; disponible sur https://hal.inrae.fr/hal-02592265/document